【基本】垂線の作図(直線上の点を通る)
ここでは、ある直線上の点を通り、その直線に垂直な直線を作図する方法を見ていきます。
直線上の点を通る垂線
垂線を作図する方法は、【基本】垂線の作図(直線上にない点を通る)その1や【基本】垂線の作図(直線上にない点を通る)その2で見ました。どちらも、次のような図を考えていました。
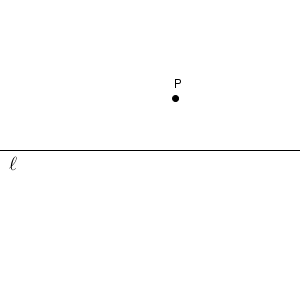
直線 $\ell$ と、この直線上にない点 P がある状況です。このときに、点 P を通り、直線 $\ell$ に垂直な直線を作図する方法を見たのでした。
このページで考えたいのは、垂直な直線の作図方法なのですが、状況が少し異なります。
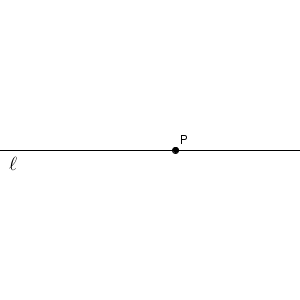
点 P は、直線 $\ell$ 上にある、という状況です。このときに、点 P を通り、直線 $\ell$ に垂直な直線を作図する方法を考えてみましょう。
直線上にない場合を参考にする方法
他の垂線の作図方法を参考にするやり方を考えてみましょう。
直線上にない点を通る垂線のうち、1つ目の方法は、次のような手順で作図するのでした。
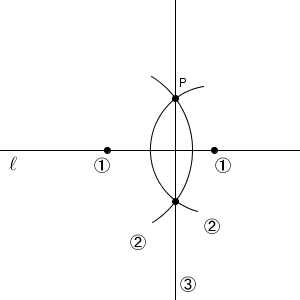
直線 $\ell$ 上に2点をとり、それらを中心として点 P を通る円をかく、そして交点を結ぶ。こういうやり方です。このやり方を、点 P が直線 $\ell$ 上にあるときに応用できるかを考えてみると、少し難しそうですね。
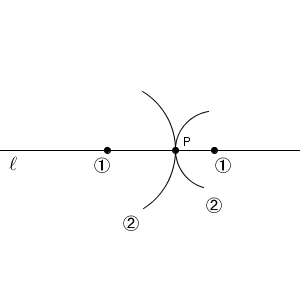
直線 $\ell$ 上の2点をとって、それらを中心として点P を通る円を2つかいても、2点で交わりません。垂線をひくことはできなさそうです。
一方、2つ目の方法は、次のような手順で作図するのでした。
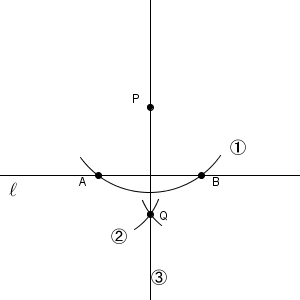
点 P を中心とした円をかき、直線 $\ell$ との交点を中心とした円をかき、その交点と点 P とを結ぶ、という方法です。この方法では、最後にできる直線は、線対称の軸となるように作ったので、直線 $\ell$ と垂直になります。
このやり方を、点 P が直線 $\ell$ 上にあるときに応用してみると、次のようになります。

点 P を中心とした円をかき、直線 $\ell$ との交点を中心とした円をかき、その交点と点 P とを結ぶ。同じ方法です。この方法でも、最後にできる直線は、線対称の軸となるので、直線 $\ell$ と垂直になります。点 P を直線 $\ell$ に近づけていく、とイメージしてもいいでしょう。
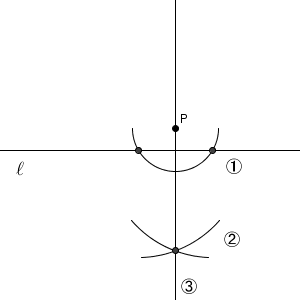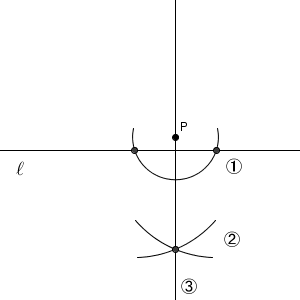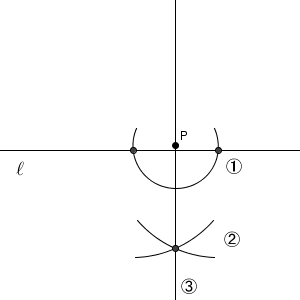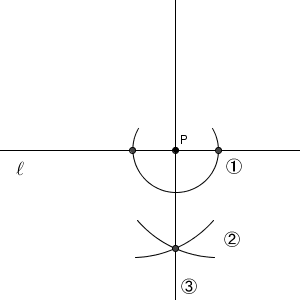
こうして、2つ目の方法を応用することで垂線をひくことができました。
角の二等分線を参考にする方法
直線上にある点を通り、その直線に垂直な直線をひく方法は、角の二等分線を参考にして考えることもできます。最終的には先ほどと同じ方法になるのですが、考え方が少し違います。
角の二等分線は、次のように作図するのでした。
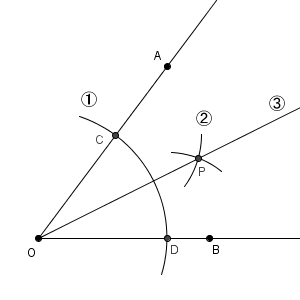
点 O を中心とした円をかき、2つの半直線との交点を中心とした円をかき、その交点と点 O とを結ぶ、という方法です。こうすることで、 $\angle \mathrm{ AOB }$ を二等分する直線が得られます。
これを利用すると、今やろうとしている作図は、次のように考えることもできます。
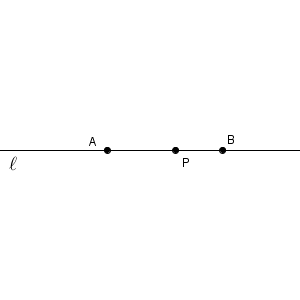
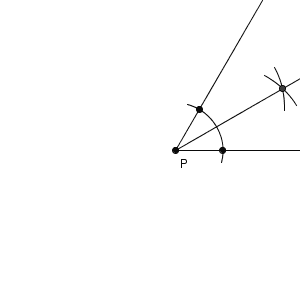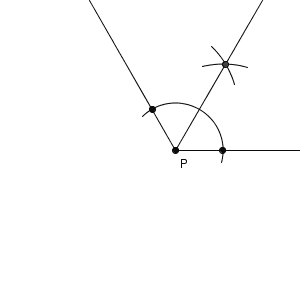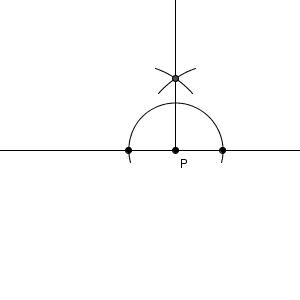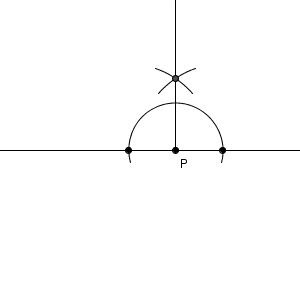
点 P を通り、直線 $\ell$ に垂直な直線とは、 $\angle \mathrm{ APB }$ の二等分線と言い換えることができます。180度を二等分するから90度になる、という発想です。角の二等分線の作図方法を真似ると、次のようになります。

点 P を中心とした円をかき、直線 $\ell$ との交点を中心とした円をかき、その交点と点 P とを結ぶ。これは、向きが違うだけで、先ほど見た方法と同じです。結果は同じですが、こちらの方法では、次のようにして角の二等分線を利用した、と考えているわけです。
角の二等分線は、180度に対して使えば90度を作図できる、ということですね。さらに使えば、45度を作ることもできます。180度は直線をひくだけで作れるので、定規とコンパスがあれば、180度、90度、45度を作り出すことができます。
垂線の作図(直線上の点を通る)
さて、ここまでの内容をまとめておきましょう。「点 P を通り、直線 $\ell$ に垂直な直線(点P は直線 $\ell$ 上の点)」の作図方法をいろいろな考え方で見てきましたが、最終的には次のような方法にまとめられます。
- STEP.1直線上に2点を作図する点 P を中心として、直線 $\ell$ と2点で交わる円をかく
- STEP.2交点からの距離が等しい点を作図する2つの交点を中心とし、同じ半径の円をかいて、交点を作る
- STEP.3垂線をひく先ほどの交点と点 P とを結ぶ
手順だけ見れば、【基本】垂線の作図(直線上にない点を通る)その2とまったく同じです。
おわりに
ここでは、ある直線上の点を通り、その直線に垂直な直線を作図する方法を見てきました。今までに見た作図を応用して考えることができました。





