【基本】2つの円と線対称な図形
ここでは、2つの円を使った線対称な図形について見ていきます。ここで見る内容は、今後、作図をするときにも利用していきます。
線対称
折り紙を折るときに、ある折り目で折れば、ぴったりと重なることがあります。このように、図形をある直線で折り返したときに、ぴったりと重なるような図形のことを、線対称(line symmetry) な図形といいます。言い換えると、ある直線について図形を反転させると、もとの図形とぴったり重なる図形、と表すこともできます。
線対称な図形はいろいろありますが、例えば二等辺三角形は線対称な図形の例です。

中央の線で折ると、左右の図形はぴったり重なります。この折り目にあたる直線のことを、対称の軸といいます。
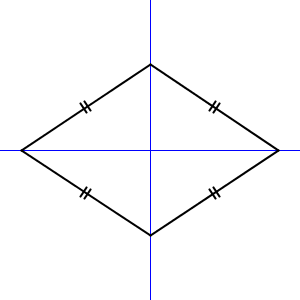
対称の軸は1つの図形に対して1本だけとは限りません。例えば、ひし形の場合は2本あります。
円にいたっては、対称の軸は無数にあります。いくつかかいてみると、次のようになります。
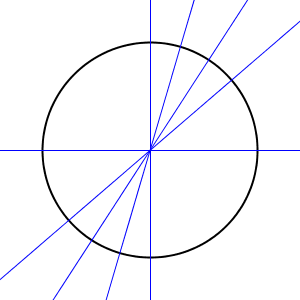
円の中心を通る直線で折ればぴったり重なるので、円の中心を通る直線が対称の軸となります。
以下では、2つの円を組み合わせた図形を見ていきましょう。
2つの円と線対称その1
2つの円が次のように2点で交わっている図形を考えてみます。
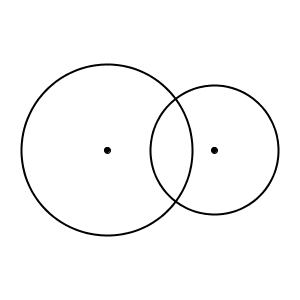
円が1つだけなら対称の軸は無数にありましたが、上のような図形だと無数ではないですね。線対称な図形であることに変わりはないですが、対称の軸は次のような1本だけとなります。
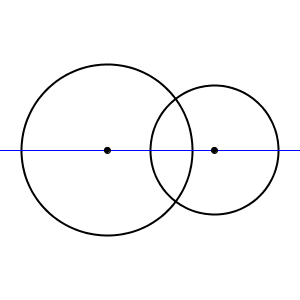
円が1つのときは、円の中心を通る直線が対称の軸でした。円が2つのときは、円の中心を両方とも通る直線が対称の軸となります。
ここで、次のように、2つの円の中心を点 A, B とおき、2つの円の交点を P, Q とおいてみましょう。

対称の軸について折り返せばぴったり重なることから、 $\triangle \mathrm{ ABP }$ と $\triangle \mathrm{ ABQ }$ は、直線 AB で折り返すとぴったりと重なります。このことから、例えば、 $\angle \mathrm{ PAB }=\angle \mathrm{ QAB }$ であることがわかります。同様に、 $\angle \mathrm{ PBA }=\angle \mathrm{ QBA }$ や $\angle \mathrm{ APB }=\angle \mathrm{ AQB }$ もわかります。
特に大事なのは、 $\angle \mathrm{ PAB }=\angle \mathrm{ QAB }$ です。これは、見方を変えると、 $\angle \mathrm{ PAQ }$ は直線 AB によって二等分される、と考えることもできます。今後、角を半分に分けたいときに、この性質を利用します。
2つの円と線対称その2
先ほどと同じ図で、今度は対角線も考えてみます。四角形 APBQ の対角線の交点を M とします。
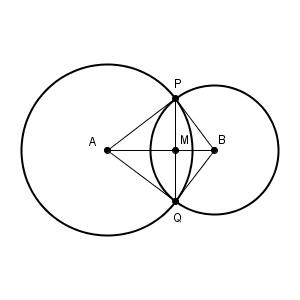
直線AB で折り返すと、 $\triangle \mathrm{ APM }$ と $\triangle \mathrm{ AQM }$ はぴったりと重なります。なので、 $\angle \mathrm{ AMP }=\angle \mathrm{ AMQ }$ がわかり、角度はどちらも $90^{\circ}$ であることがわかります。
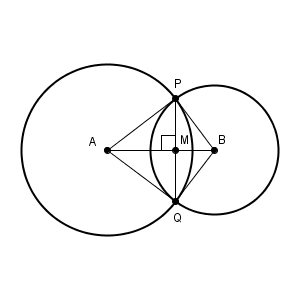
言い換えると、 $\mathrm{ AB }\perp \mathrm{ PQ }$ ということですね。この性質は、今後、 $90^{\circ}$ を作りたいとき、垂線をかきたいときなどで利用します。
2つの円と線対称その3
最後に、先ほどの図で、2つの円の半径が同じならどうなるかを見てみましょう。
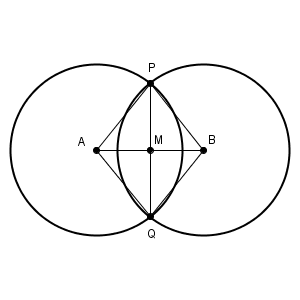
この場合、対称の軸が2本になります。直線 AB だけでなく、直線 PQ も対称の軸となります。上下がぴったり一致するだけでなく、左右にもぴったり一致します。

そのため、直線 PQ で折り返すと、 $\triangle \mathrm{ APM }$ と $\triangle \mathrm{ BPM }$ はぴったりと重なります。なので、 $\mathrm{ AM=BM }$ となることがわかります。
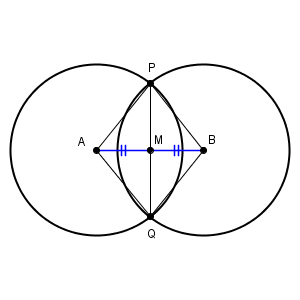
見方を変えれば、直線 PQ は、線分 AB を半分の長さになるように分けている、とも考えられます。この性質は、今後、線分の長さを半分にしたいときに利用します。
おわりに
ここでは、今後の作図で利用できる、2つの円に関連する線対称の性質について見てきました。角を半分にする、直角を作る、線分を半分にする、というときに、これらの性質を利用することになります。どのように利用するかは、別のページで詳しく見ていきましょう。





