【標準】3点を通る円の作図

ここでは、3つの点を通る円の作図方法を見ていきます。

3点を通る円の作図

円をかくには、中心と半径が必要です。どちらもわかりませんが、中心さえわかれば半径はわかります。半径は中心から A までの距離ですからね。

そこで、中心がどこかを考えてみましょう。中心 O は、どのような条件を満たさないといけないでしょうか。もし、作図できたとしたら、次のようになるはずです。

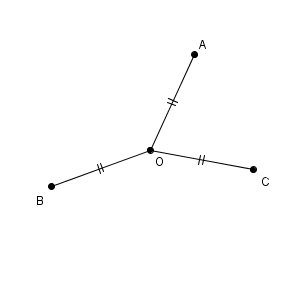
円が3点を通ることから、中心からこの3点までの距離はすべて等しいことがわかります。これが円の中心が満たさないといけない条件です。

これだけではわかりにくいですが、「2点からの距離が等しい」という条件であれば、【標準】垂線や二等分線の作図で見ています。2点 A, B からの距離が等しい点の集まりは、線分 AB の垂直二等分線上にあるのでした。

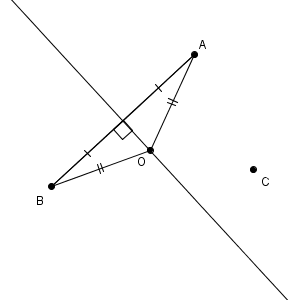
さらに、 B, C からの距離が等しい点の集まりは、線分 BC の垂直二等分線上にあることになります。

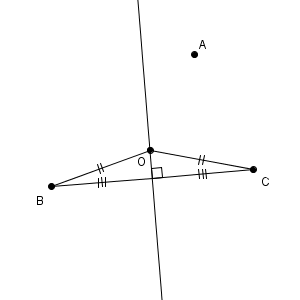
なので、2つの垂直二等分線の交点は、3点 A, B, C からの距離が等しい点であることがわかります。つまり、これが円の中心ということです。

以上を踏まえて作図をしていきます。垂直二等分線を2回かきます。交点が O となります。そして、 OA を半径とする円をかけばいいわけですね。

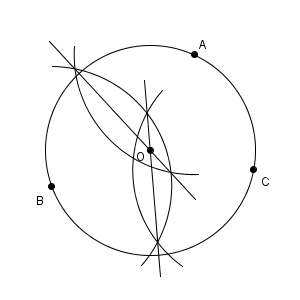
少しごちゃごちゃしているので、分解してかくと次のようになります。まず、線分 AB の垂直二等分線をかきます。

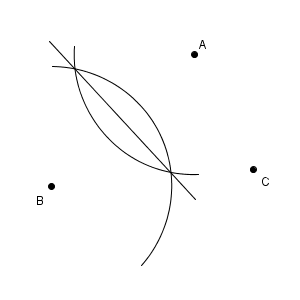
次に、線分 BC の垂直二等分線をかきます。

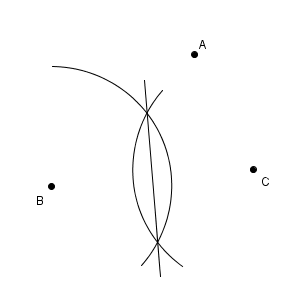
ここでは、B を中心とした弧を大きくかいて、2本の垂直二等分線の作図で使いまわしています。ただ、線分 AB の垂直二等分線をかくときに使う半径と、線分 BC の垂直二等分線をかくときに使う半径は、異なる長さでも構いません。

この2本の垂直二等分線の交点が、円の中心 O となります。あとは、 O を中心として半径を OA の長さにした円をかけば、3点を通る円がかけます。

なお、ここでは、 AB, BC の垂直二等分線をかきましたが、 AC の垂直二等分線を使っても、円の中心を作図することができます。下の図は、 AB, AC を使って作図したものです。

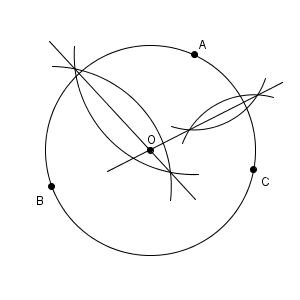
2つの垂直二等分線をどのように選んでも、交点が3点からの距離が等しい点であることに違いはありません。

外接円

先ほどの例題は、次のように出題されることもあります。

外接円(circumcircle) というのは、すべての頂点を通る円のことです。つまり、3点 A, B, C を通る円、ということなので、先ほどの例題と同じ作図方法で答えが得られます。

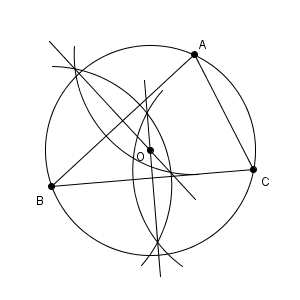
一般に、三角形に対して、2つの辺の垂直二等分線をひくと、交点が必ずできます。もしできないとすると、2つの垂直二等分線は平行となり、2つの辺が一直線上にないといけなくなってしまいますが、それだと三角形ができないのでおかしくなります。なので、交点は必ずできます。

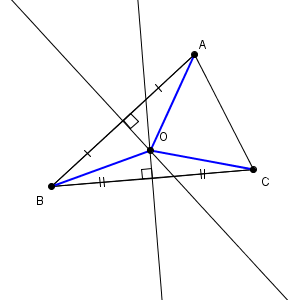
このように交点を作ると、3つの頂点からの距離（3本の青い太線の長さ）が等しいので、どんな三角形に対しても、この交点を中心とした外接円がかけることがわかります。また、3つの辺に対して垂直二等分線をひくと、外接円の中心で交わることもわかります。

一般的には、3本の線が1点で交わるとは限りませんが、三角形の3つの辺の垂直二等分線は、1点で交わるんですね。なかなか面白い性質です。

三角形には、他にもいろいろなきれいな性質があるのですが、それは、今後、徐々に見ていくことになります。

おわりに

ここでは、3点を通る円の作図方法を見てきました。また、三角形の外接円をかくときにも、同じ方法で作図できることを見ました。「2点からの距離が等しい点の集まり」を2回使って作図しましょう。