【標準】折り目の作図

ここでは、図形を折ったときの折り目を作図する問題を見ていきます。

折り目

折り紙で何かを作ったことがある人はわかると思いますが、紙を折ってから広げると、線がつきます。この線のことを、折り目といいます。作図の問題では、折り目を作図することもあります。

例えば、次のような、 $\mathrm{ AB=AC }$ である二等辺三角形があったとして、点 B が点 C に重なるように折るとしましょう。

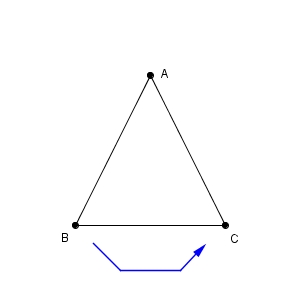
このときに、折り目はどのようになるでしょうか。この場合は、折ったときには元の図形のちょうど半分となるので、折り目は、辺 BC の垂直二等分線になることがわかります。

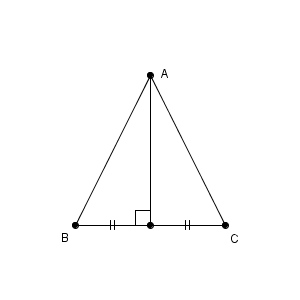
あとは、垂直二等分線の作図を行えばおしまいです。

では、同じ図形で、今度は、点 A が、線分 BC の中点 M に重なるように折った場合の折り目はどうなるでしょうか。

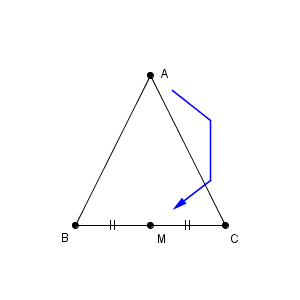
折る前の部分と、折った後の部分を色を付けて塗り分けると、次のようになります。点 A を含む側を動かすとして、折る前を青、折った後を赤で表しています。

これは、よく考えれば当たり前ですが、折る前の部分と折った後の部分は同じ図形になります。折り目にそって折り返しただけなので、同じ図形であることには変わりはありません。言い換えると、折り目は、対称の軸になっている、と考えることもできます。

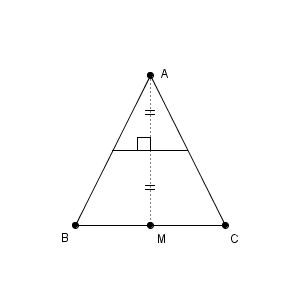
つまり、この場合の折り目は線分 AM の垂直二等分線になっている、ということです。点 A と点 M が重なるようにするには、線分 AM の垂直二等分線で折ればよく、それ以外の場合は2点が重なることはありません。

このことから、ある点とある点が重なるように折る場合、折り目は2点を結んだ線分の垂直二等分線になることがわかります。折り目が対称の軸になっている、と考えましょう。

例題１

丸い紙を折ることは少ないと思うので、少しイメージしにくいかもしれません。折り返す前と後で色を付けて表すと、次のようになります。点 P を含む側を折り返す、と考えています。

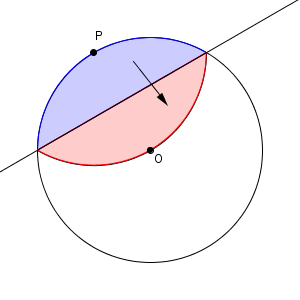
これも、折り返す前と後では同じ図形になります。そのため、折り目は、線分 OP の垂直二等分線をかけばいいことがわかります。

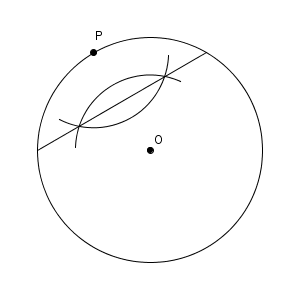
これが答えとなります。

例題２

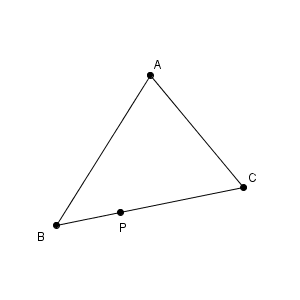
図形に対称性がないため、折り目がどうなるか想像しづらいですが、これも考え方は同じです。折る前と後では図形が同じなので、折り目が対称の軸となります。そのため、折り目は、線分 AP の垂直二等分線をかけばいいです。

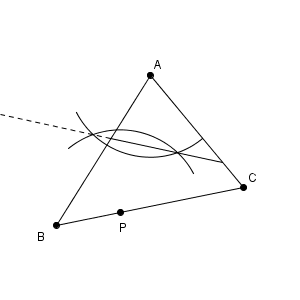
このようになります。

点はどこに移動するか

最後に、逆に折り目から点がどこに移動するかを考えてみます。

次の図のような長方形 ABCD があって、対角線 BD で折り返すとします。

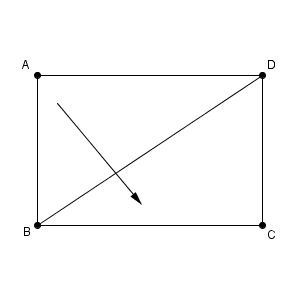
このとき、点 A を含む側を動かすとして、点 A が点 P に移動したとします。

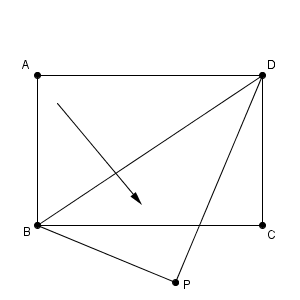
この点 P はどのように作図すればいいでしょうか。

今まで見たように、 BD が対称の軸となっていることを使えば、 AP と BD は垂直であることがわかります。そのため、 A を通り、 BD に垂直な直線をかけば、その直線のどこかに点 P があることがわかります。

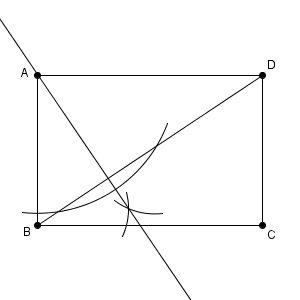
さらに、 BD から A までの距離と P までの距離は等しいことがわかるので、これを使えば点 P の場所がわかります。

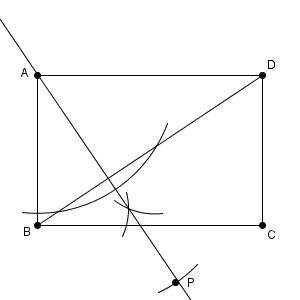
A から BD に引いた垂線と BD との交点を中心として、点 A を通るように円をかいて、垂線との交点を点 P としています。

このように作図することもできますが、【基本】垂線の作図（直線上にない点を通る）その１で見た内容を使うこともできます。点 B 、点 D を中心として、点 A を通る円をかきます。

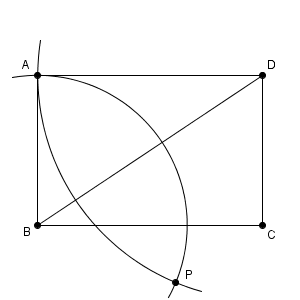
この交点が P となります。上のリンク先で見たように、四角形 ADPB は BD について線対称なので、折り返せばぴったりと重なることからわかります。

おわりに

ここでは、折り目の作図方法について見てきました。何かを折ると、折る前の部分と折った後の部分は同じ形になります。このことから、折り目が対称の軸であると考え、垂直二等分線をかけばいい、と考えることが重要です。