【基本】角の二等分線の作図

🕒 2019/07/14 🔄 2023/05/01

ここでは、角の二等分線の作図方法を見ていきます。

📘 目次

角の二等分線

角の二等分線とは、次の図の青線のように、1つの角を二等分する半直線（または、直線）のことです。

上の図では、$\angle \mathrm{ AOP }=\angle \mathrm{ BOP }$ なので、直線 OP は、 $\angle \mathrm{ AOB }$ の二等分線である、といいます。どちらの角も $\angle \mathrm{ AOB }$ の半分なので、文字を使った数式のように\[ \angle \mathrm{ AOP }=\angle \mathrm{ BOP }=\frac{1}{2}\angle \mathrm{ AOB } \]と表すこともあります。

角の二等分線について、最も典型的な作図の問題は、ある角が与えられたときに、「この角の二等分線を作図しなさい」というものです。上の図で言えば、半直線 OA, OB が与えられたときに、半直線 OP を作図する、ということです。 O の場所はわかっているので、角の二等分線上の点のどれかの場所がわかればいいですね。つまり、点 P が作図できればいいです。

見方を変えると、上の図は、角の二等分線を軸として線対称である、と考えることもできます。OP で折れば、 OA と OB が重なるからですね（長さが異なるかもしれませんが）。そこで、線対称な図形を利用することにします。

作図では、定規とコンパスしか使えないのでした。垂線の作図（参考：その１、その２）では、コンパスでかいた2つの円をかき、これが線対称であることを利用していました。利用していたのは、次の図です。

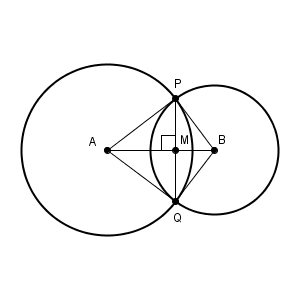
この図では、直線 AB で折り返せば、2点 P, Q が重なるので、 $\mathrm{ AB }\perp \mathrm{ PQ }$ となります。このことを用いて、垂線をかいたのでしたね。

角の二等分線でも、この図を利用することができます。角とその二等分線がどのように表れているか、そして、どう作図すればいいかを考えてみましょう。

角の二等分線の作図方法

先ほどの線対称な図をもう一度見てみましょう。

この図で、直線 AB が線対称の軸です。 $\angle \mathrm{ PAQ }$ を見れば、直線 AB によって、二等分されることがわかります。これを利用して、角の二等分線を作図してみましょう。この図を次のように回転すれば、点や円がどのように対応しているかわかると思います。

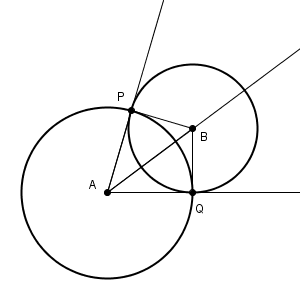
いくつか不要な線を消したり、線を伸ばしたりしています。これを参考にしながら、角の二等分線の作図方法を見ていきます。

次の図で、 $\angle \mathrm{ AOB }$ の二等分線を作図します。

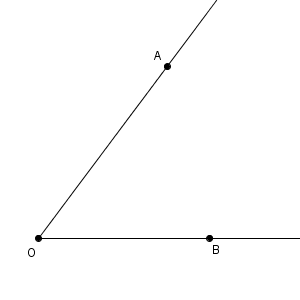
参考図と比較すると、点 O が左側の円の中心で、角の二等分線が線対称の軸に対応しています。参考図の点 P の場所がわかればいいわけですね。

そこで、まず、左側の円をかくことにしましょう。点 O を中心とし、半径は何でもいいので、次のようにかきます。

OA, OB とそれぞれ1点ずつ交わります。交わればいいので、円の一部だけをかけば十分です。

この2点が、参考図での2円の交点に対応していると考えます。後は、右側の円の中心がどこかがわかればいいですね。これは、「2つの交点から同じ距離だけ離れている」と考えれば、それぞれの交点を中心とする円をかけばいいことがわかります。

これも、交点がわかればいいので、円の一部だけをかきます。

あとは、この交点と点 O を結んでおしまいです。

この方法でどうしてうまくいくのか、点に名前をつけて、もう少し考えてみましょう。

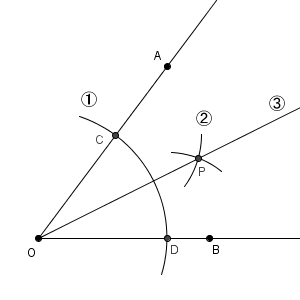
点 O を中心とした円をかいて、それと直線 OA との交点を C、直線 OB との交点を D とすると、 $\triangle \mathrm{ CDO }$ は二等辺三角形となります。さらに、点 C, D から同じ半径の円をかいて交点を P とすれば、 $\triangle \mathrm{ CDP }$ も二等辺三角形です。

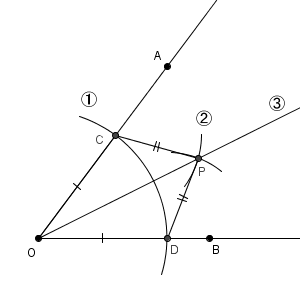
そのため、四角形 OCPD は、直線 OP について線対称であることがわかります。直線 OP で折ると、ぴったり重なるからですね。こうして、 $\angle \mathrm{ COP } = \angle \mathrm{ DOP }$ であること、つまり、直線 OP が $\angle \mathrm{ AOB }$ の二等分線であることがわかります。

最後に、「$\angle \mathrm{ AOB }$ の二等分線」のかきかたをまとめておきましょう。