【標準】複素数平面と同一直線上にある3点

🕒 2019/02/16 🔄 2023/05/01

ここでは、複素数平面上で、3点が同一直線上にあるときや、2直線が垂直に交わるときについて見ていきます。

📘 目次

3点が同一直線上にあるとき

複素数平面上で、異なる3点 A$(\alpha)$, B$(\beta)$, C$(\gamma)$ が、同一直線上にあるための条件について考えてみましょう。

これは、【基本】複素数平面と2直線のなす角で見た内容を応用することができます。 $\angle \mathrm{ BAC }$ は、対応する複素数を使って次のように書けるのでした。\[ \arg\frac{\gamma-\alpha}{\beta-\alpha} \]同一直線上にあるということは、 $\angle \mathrm{ BAC }$ は $0$ か $\pi$ ということです。 A からみて、 B と C が同じ側にあるなら $\angle \mathrm{ BAC }=0$ となり、反対側にあるなら $\angle \mathrm{ BAC }=\pi$ となります。いずれにしても、 $\dfrac{\gamma-\alpha}{\beta-\alpha}$ の虚部は $0$ なので、これが実数であるときだ、と言い換えることができますね。

また、直線 AB と AC が垂直に交わるときは、偏角が $\pm\dfrac{\pi}{2}$ のときなので、 $\dfrac{\gamma-\alpha}{\beta-\alpha}$ の実部が $0$ のとき、つまり、純虚数のときだとわかります。

同一直線上にある3点、垂直に交わる2直線（複素数平面）

複素数平面上で、異なる3点 A$(\alpha)$, B$(\beta)$, C$(\gamma)$ について、次が成り立つ。
3点 A, B, C が同一直線上にあることは、 $\dfrac{\gamma-\alpha}{\beta-\alpha}$ が実数であることと同値である。
2直線 AB, AC が垂直に交わることは、 $\dfrac{\gamma-\alpha}{\beta-\alpha}$ が純虚数であることと同値である。

なお、実数であること、純虚数であることを計算によって確かめるには、【標準】共役複素数と複素数の実数条件で見た内容が使えます。実際に、次の例題で見ていきましょう。

3点が同一直線上にあるときを求める

例題

$t$ を実数とします。複素数平面上の3点 $\mathrm{A}(t+i)$, $\mathrm{B}(1)$, $\mathrm{C}(3i)$ について、以下の問いに答えなさい。
(1) 3点 A, B, C が同一直線上にあるとき、 $t$ の値を求めなさい。
(2) 点 A が、線分 BC を直径とする円の上にあるとき、 $t$ の値を求めなさい。

先ほど見た内容を使って考えてみましょう。

(1)は、 $\angle \mathrm{ BAC }$ が $0,\pi$ であるときを求めればいいですね。(2)は、 $\angle \mathrm{ BAC }$ が $\pm\dfrac{\pi}{2}$ であるときを求めればいいです。どちらの場合も、\[ \frac{3i-(t+i)}{1-(t+i)} \]について考えればいいですね。これが実数のときが(1)の答え、純虚数のときが(2)の答えです。なので、まずは、この式を変形していきましょう。

\begin{eqnarray} & & \frac{3i-(t+i)}{1-(t+i)} \\[5pt] &=& \frac{-t+2i}{1-t-i} \\[5pt] &=& \frac{(-t+2i)(1-t+i)}{(1-t-i)(1-t+i)} \\[5pt] &=& \frac{(-t+t^2-2)+(-t+2-2t)i}{(1-t)^2+1} \\[5pt] &=& \frac{(t^2-t-2)+(-3t+2)i}{(1-t)^2+1} \\[5pt] \end{eqnarray}となります。ここで、分母は実数なので、分子について考えればいいですね。

(1)の答えは、この値が実数のときを求めればいいので、虚部が $0$ となるときが答えですね。 $-3t+2=0$ より\[
t=\frac{2}{3} \]となります。これが答えです。

(2)の答えは、純虚数になるときを求めればよく、実部が $0$ になるときを考えればいいです。
\begin{eqnarray} t^2-t-2 &=& 0 \\[5pt] (t-2)(t+1) &=& 0 \\[5pt] t &=& 2,-1 \end{eqnarray}となります。よって、これが答えです。

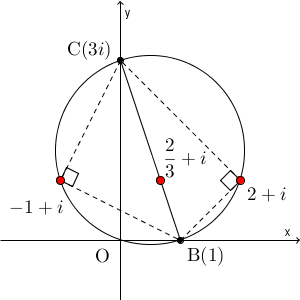
複素数平面を使わずに、座標平面で考えることもできます。 $\mathrm{A}(t,1)$, $\mathrm{B}(1,0)$, $\mathrm{C}(0,3)$ とすると、直線 BC の方程式は\[ y=-3x+3 \]となります。(1)については、点 A がこの直線上にあるとすると\[ 1=-3t+3 \]を解いて $t=\dfrac{2}{3}$ となります。

一方、(2)は、線分 BC を直径とする円の方程式を求めて、それが点 A を通るときを考える、という解き方があります。また、ほとんど同じことですが、 BC の中点と点 A との距離が、線分 BC の半分、と考えてもいいでしょう。

この例題では、点に関する情報がわかりやすいので、座標平面で考えても解ける（というか、むしろそちらの方が簡単）のですが、抽象的な場合には、複素数平面で考えたほうが楽になることもあります。