整数の定義
自然数や自然数の加法などを定義してきたので、次は整数の定義を行っていきます。
整数は何だと教わってきたか
中学のときに、 $-1$ などの負の整数が出てきました。自然数の世界から数の範囲を広げました。
自然数は主に個数を数えるときに使いましたが、負の整数は「数は個数」という考えからは生まれません。「基準からの位置を表すときに使うため」という、個数とは違った考え方で導入されることが多いです。
時間でいえば、今日を基準とすると、明日は +1で、昨日は -1と書ける、というような具合です。気温や高度、収支などでも、「基準からの位置」を表すときには、負の数が使えるよね、と。
また、負の整数まで世界を広げるのは、「引き算をいつでもできるようにするため」だと説明されることもあります。 $1$ から $3$ を引くことは、自然数の範囲ではできませんが、負の整数まで範囲を広げると、 $-2$ と計算できます。
このように、高校までの数学では、自然数から整数へと数の範囲を広げるときには、「基準からの位置を表すのに使える」「引き算がいつでもできる」などと言って導入されてきました。
現代数学では、自然数が、数学の言葉を使って定義されていることを見ました(参考:自然数の定義)。整数も、数学の言葉を使って抽象的に定義されています。もちろん、今までに扱ってきた整数の性質と整合的になるように定義されています。
整数をどうやって定義するか
このシリーズでは、自然数の加法 や 自然数の乗法は定義しましたが、まだ自然数の引き算を定義していません。なので、厳密にはまだ引き算は使えないのですが、高校までに使っていた引き算を用いて、整数をどう定義するかを考えていきましょう。なお、最終的には、このシリーズで定義した内容だけを使って整数を定義することになります。
中学のときに負の整数を導入したことで、引き算がいつでもできるようになりました。例えば、負の整数を導入することで、 $1-3$ は $-2$ と計算できるようになります。
$-2$: $1-3$
ここで、このシリーズではまだ引き算を定義していなかったので、単純に、 $1$ と $3$ のペアに対して $-2$ を対応させる、と考えてみることにしましょう。このペアのことを、 $(1,3)$ で表すことにします。
$-2$: $(1,3)$
自然数はすでに定義しているので、これを使えば、整数が定義できそうです。つまり、「整数1個」を表すために、「自然数2個のペア」を使うということです。 $(1,3)$ というペアで、 $-2$ を表していると考えることにするよ、というわけです。この2つの数字は、並び順にも意味があります。 $(3,1)$ なら $2$ を表すことになります。
高校のときに、複素数について学びました。このとき、1つの複素数を表すために実数を2つ使いました。「あるものを表すのに、何か2つを使って表す」という手法は、他にも、分数や座標など、今までにも何度か出てきています。
整数1個を自然数2個で表す、というのは、はじめは変に感じるかもしれませんが、複素数や分数などの例を考えると、受け入れやすいと思います。
ただ、ここで一つ問題があります。整数1個に対応させる「自然数2個」の選び方は1通りではない、という点です。先ほどの発想を使えば、例えば $-2$ は他にも次のような表し方があります。
$-2$: $(2,4)$
$-2$: $(5,7)$
$-2$: $(10000,10002)$
困りましたね。何か1つに決めたほうが便利そうなのですが、恣意的に「この表し方を使う」と決めてしまうのもあまりよくありません(こういうとき、数学をやってる人は「きれいじゃない」とか「美しくない」と言ったりします)。
そこで、数学の世界ではどうするかというと、「グルーピングしちゃおう」と考えます。同じものを表すペアは、1つにまとめてしまうのです。同一視する、ともいいます。
例えば、 $(1,3)$ と $(2,4)$ は同じ $-2$ を表すことになってほしいです。こういうケースについて少し考えてみましょう。これは、引き算で考えると、次のように表せることに対応します。\[ 1-3=2-4 \]移行をすると、次のようになります。\[ 1+4=2+3 \]$(1,3)$ と $(2,4)$ の外側同士、内側同士の和が等しいという式です。この両辺は、自然数の加法なので、本シリーズですでに定義しています(参考:自然数の加法)。
これを踏まえると、整数は、次のように考えるのがよさそうです。
- 自然数 $a,b$ を使って、 $(a,b)$ が1つの整数を表す、と考える。
- 別の自然数のペア $(c,d)$ が\[ a+d=c+b \]を満たすなら、 $(a,b)$ と $(c,d)$ は同じ整数を表していると考える。
このようにすれば、今まで定義したものだけを使って、整数を $a-b$ のつもりで表すことができると考えられます。 $a-b=c-d$ は $a+d=c+b$ と同じことなので、こうなるペア同士が同じ整数を表すと考えるのは自然でしょう。
「何通りも表し方があると、困ることは起きないのだろうか? 整合性はとれるのだろうか?」と疑問に思う人もいるかもしれません。実は、ここは少し注意しないといけなくて、今後の議論でも常に気にしておく必要があります。その都度、説明していきます。
また、「1つのものを表すのに、何通りも表し方があるのって、そもそもおかしくない?」と思う人もいるかもしれません。しかし、実はこうしたものはすでに小学校で習っています。分数です。 $\dfrac{1}{2}$ も $\dfrac{2}{4}$ も $\dfrac{50}{100}$ も同じ値ですが、表し方はたくさんあります。これと似た発想を使っている、と考えると理解しやすいでしょう。
図で考えてみよう
整数の定義についてさらに細かく見ていく前に、どういうことをやっているか、図でイメージをつかみましょう。
整数1個を決めるために、自然数2個のペア $(a,b)$ を使うのだから、図では、2次元での点に対応していると考えるとわかりやすいです。( $0$ も自然数としています)

これらの点を全部使うことになったわけです。
ただ、 $a+d=c+b$ を満たすもの、引き算で書けば $a-b=c-d$ を満たすものは、同一視するのでした。これは、直線 $y=x$ に平行な直線を次のようにかいた場合、同じ直線上にあるものはぜんぶ同一視する、と言うわけです。

先ほど、 $(1,3)$ と $(2,4)$ が同じ整数を表すことを見ましたが、上の図では、この2点が同じ直線にあることに対応しています。
さらに言い換えると、それぞれの直線は $x$ 軸上の整数の点に対応している、と考えることもできるでしょう。
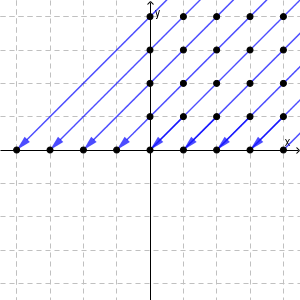
直線 $y=x$ に沿って $(a,b)$ を平行移動すると、 $x$ 軸とは $(a-b,0)$ で交わります。このような対応だとわかれば、自然数のペアをまず考えて、それをグルーピング(直線 $y=x$ に平行な "ある直線" 上にあれば、それらの点を同一視)したものを、整数に対応させるのは、そんなに難しいことをやっているわけではないことがわかります。
整数はちゃんと定義できているか
さて、整数の定義の話に戻りましょう。
自然数 $a,b$ を使って、 $(a,b)$ で1つの整数を対応させる、しかも、他の自然数のペア $(c,d)$ が $a+d=c+b$ を満たしていれば、 $(a,b)$ と $(c,d)$ は同じだとみなす。このように定義すればいいのではないか、という話でした。
こうすれば、$(a,b)$ と等しいものを全部ひっくるめて、それら全部を $a-b$ のことだと思うようにすれば、たしかに整数だと考えられるような気がします。先ほどの図でいえば、各直線に整数を対応させていく、というイメージです。
これを表すために、次のような記号を導入しましょう。
自然数のペアで、 $(a,b)$ と同じグループになるものを集めた集合を $[(a,b)]$ で表すことにします。つまり、\[ [(a,b)] = \{ (c,d) \mid a+d=c+b \} \]ということです。わかりやすく言えば、 $a-b$ が同じ結果になるものをまとめたもの、ということですが、引き算を定義していないのでこういう書き方をしています。
この $[(a,b)]$ が $a-b$ に対応する整数を表していると考えるようにすれば、整数が定義できたと言えそうです。
しかし、このように考えるには、モレやダブりがないことを確認しておかなくてはいけないでしょう。
つまり、「対応させる整数が1つもない」とか、「2つ以上の整数に対応できてしまう」といった問題が起きないことを確認しておく必要があります。
先ほどのように図で考えれば、こういうケースはありえなさそうですが、式を使ってきちんと確認しておきましょう。
まず、1つ目の「モレがない」について考えます。次のようなケースを心配しています。

$(c,d)\in [(a,b)]$ は、 $a+d=c+b$ となることと同値です。 $c=a, d=b$ とすれば、この式は $a+b=a+b$ となりますが、これはもちろんいつでも成り立ちます。つまり、 $(a,b)\in[(a,b)]$ ということです。
少なくとも、自分は「自分と同じグループ」に属することがわかります。つまり、どの自然数のペアも、どこかのグループに属していることがわかります。モレはない、ということです。
次に、「ダブりがない」について考えましょう。
$a+d\ne c+b$ と仮定します。このときに、あるペアがどちらのグループにも属していると困ってしまいます。つまり、次のようなケースを心配しています。

こういうことがないことをチェックしましょう。
もし、 $(e,f)\in[(a,b)]$ と $(e,f)\in[(c,d)]$ が同時に成り立っていたとしましょう。このとき、 $a+f=e+b$ と $c+f=e+d$ が成り立ちます。2つ目の両辺を入れ替えて、1つ目の式に辺々足すと\[ (a+f)+(e+d)=(e+b)+(c+f) \]となりますが、簡約法則を使って $e+f$ を取り除くなどをすると\[ a+d=c+b \]となり、仮定と矛盾します。なので、 $(e,f)\in[(a,b)]$ と $(e,f)\in[(c,d)]$ は両方同時には成り立たない(片方だけが成り立つか、どちらも成り立たない)ことになります。
これは、 $(e,f)$ が、異なる2つのグループに属していない、グループがダブっていない、ということを表しています。
これで、モレもダブりもないことがわかりましたが、最後に、そもそも、このグループが確定することも確認しておきましょう。つまり、
$a+d=c+b$ ならば、 $[(a,b)]$ と $[(c,d)]$ は一致する
も確認しておかなくてはいけません。これが成り立たないなら、どのペアから考え始めるかでグループのメンバーが変わり、確定しないことになってしまいます。つまり、次のようなケースを心配しています。

こういうケースが起こらないことを示します。つまり、 $a+d=c+b$ とし、 $(e,f)\in[(a,b)]$ としたときに、 $(e,f)\in[(c,d)]$ となることを示しましょう。
$(e,f)\in[(a,b)]$ とすると、 $a+f=e+b$ が成り立ちます。また、仮定より $a+d=c+b$ です。両辺を入れ替えると $c+b=a+d$ となり、辺々加えると\[ (a+f)+(c+b)=(e+b)+(a+d) \]が成り立ちます。加法の結合法則や交換法則、簡約法則から、 $a+b$ を両辺から取り除いて\[ c+f=e+d \]が導けます。これは $(e,f)\in[(c,d)]$ ということです。
逆も同じように示せます。これより、 $[(a,b)]$ と $[(c,d)]$ は、片方に属している元すべてがもう片方にも属していることがわかるので、集合として同じになります。
こうして、各 $[(a,b)]$ は、同じ整数 $a-b$ を表すものたちで構成され、 $[(a,b)]$ たちを集めたものは、自然数のペアを、モレもダブりもなく分割できていることになります。この各 $[(a,b)]$ に $a-b$ を対応させる、と考えて、整数は次のように定義します。
もはや、数がまったく出てきていませんが、これが整数の定義です。
専門書によっては、ここはもっと集合論の言葉を使った書き方で定義されていることでしょう。
集合論の言葉を使えば、\[ (a,b)\sim(c,d) \iff a+d=c+b \]という同値関係 $\sim$ を定義する、という話がまず出てきます。これは、この記事でいうと、「どういう自然数のペアを同一視するか?」というルールを決めている、ということです。
次に、同値類 $[(a,b)]$ を考える、という話が出てきます。これは、 $(a,b)$ と同じ整数を表すことにしたいペア全体をまとめた集合、ということです。
最後に、「 $\mathbb{N}\times\mathbb{N}$ をこの同値関係で割って得られる商集合を、整数の集合という」といった話が出てきます。商集合とは、この記事でいうと、自然数のペアの集合を分割していくことに対応しています。
このような、「同一視するためのルール(同値関係)を決めて、集合を分割する(商集合を考える)」ことは、数学ではよく行います。詳しくは、集合論を将来学んだときに見ることになるでしょう。
おわりに
ここでは、自然数を2つ使って整数1つを表すことで、整数を定義する、という話を見てきました。これをもとに、整数の加法や乗法などを定義し、減法も定義していきます。