自然数の定義

ここでは、ペアノの公理を説明し、自然数の定義を行っていきます。

数字はただのラベル

日本の歴史を勉強したことがある人なら、関孝和という人を知っているでしょう。江戸時代の数学者です。この時代の数学は、漢数字を使っていました。アラビア数字に慣れてしまった現代人からすると、すごく読みづらそうです。

ところで、高校数学の教科書を見ると、「 $1,2,3\cdots$ を自然数という」などと書かれています。もしこれが他の形、例えば、漢数字だとどうなるでしょうか。自然数とは言えないのでしょうか。

そんなことはないはずです。 $1,2,3,4$ が 一、二、三、四 となっただけで、それぞれが1つ1つ対応しているのだから、同じものだと考えてもいいでしょう。置き換えれば、同じ議論ができるはずです。

例えば、下の資料を見てみましょう（括要筭法 4巻 | 京都大学貴重資料デジタルアーカイブより）。

漢数字ではなく、算木数字というものが使われています。アラビア数字との対応は、Wikipedia の算木#算木数字で、次のように記載されています。

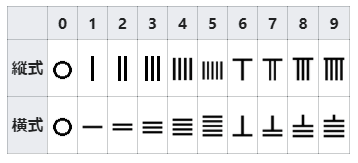
これを踏まえ、先ほどの資料を見ると、表の形から何かを思い出しませんか？　向きが違いますが、これはパスカルの三角形（参考：【基本】n乗の展開とパスカルの三角形）です。

例えば、画像の右下をみると「1,1」「1,2,1」「1,3,3,1」「1,4,6,4,1」という、パスカルの三角形の上側にある数字の並びと一致しています。また、画像の左上の方にある「丄丅」は 66 のことですが、これは ${}_{12}\mathrm{C}_2=66$ のことです。

和算にもパスカルの三角形があったんですね。表記は違いますが、アラビア数字で書いたものと対応しています。

同様に、ローマ数字で表されていたとしても、中身は同じはずでしょう。

つまり、「 $1,2,3,\cdots$ 」というのが自然数なのではなく、これは自然数を表すものとして貼り付けられた、ただの「ラベル」にすぎない、ということです。もっと奥深いところに「自然数の構造」というものがあり、個々の要素に貼り付けられたラベルがたまたま「 $1,2,3\cdots$ 」であったというだけです。

このラベルが、アラビア数字であっても、漢数字であっても、ローマ数字であっても、「いち、に、さん、…」と読んでも、「ワン、ツー、スリー、…」と読んでも、構造が同じであれば、変換することで、同じ議論がそのまま使い回せるはずです。

では、その自然数の構造とはどのようなものでしょうか。今までに扱ってきた自然数の性質を思い出しながら考えていきましょう。

自然数はどうあるべきか

今まで、自然数がどういう場面で使われてきたかを考えると、やはり個数を数える場面でしょう。例えば、次のような図があったとします。

点が何個あるかを数えようと思ったら、このように順番に数を割り当てていくでしょう。

これが、まさに先ほどの「ラベルを貼る」ことに対応している感じがしますね（個数を数えているので、1からスタートしています）。このラベルの貼り方をよく見てみましょう。

どのように数えることもできますが、まずどこかを出発点として、次へ次へと進んでいきます。一度数えたものは再び数えません。

このようにラベルをはがすと、これが自然数の構造を表しているように考えられます。これを参考にして、自然数がどのような構造を持っているべきかを考えてみます。新しく自然数を定義するために、まずは、高校までで扱ってきた「自然数」について考えていきます。

まず、どのようにラベルを貼るとしても、「スタート」が必要です。

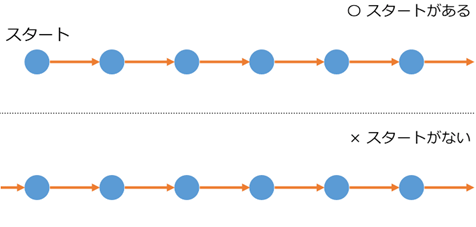
上の図の下側のように、どこからともなく列がはじまっているものは、自然数とは言えないでしょう。

そして、ラベルを貼ると、次にラベルを貼る場所が1つある、というのもポイントです。次にラベルを貼れる場所が必ずあり、しかもその場所が1個であることが重要です。

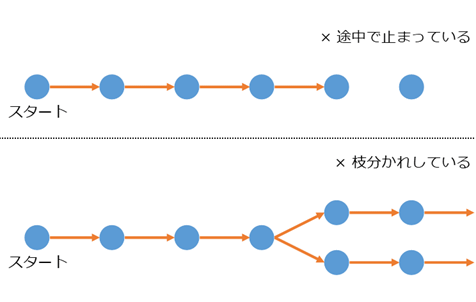
次がなかったり、枝分かれしているものは自然数とは言えないでしょう。

スタートがあって、その次、その次、と決めていくことができれば、それは自然数の構造を表しているような感じがしてきます。

しかし、実際には、この2つのルールだけでは「自然数」とは言えない構造も混じってしまいます。例えば、次のような状況はダメそうです。

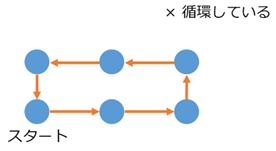
スタートから出発して、次へ次へと進んでいってるのですが、途中でスタートに戻ってしまっています。こういう循環しているケースは除外したいですね。例えば、「6で割った余りの世界」を考えると上のような図になるのですが、これは自然数の構造とは言えないでしょう。

スタートに戻るだけでなく、他のところに戻るのもダメです。

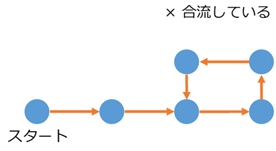
今までの流れに合流してしまうケースですね。これもダメです。今の場所が違っていたら、次の場所同士も異なっていてほしいです。

これらのダメなケースを除外すれば、確実に「新しい次の場所」へと進んでいきます。これで、自然数の構造が表せているような気がします。

と行きたいところですが、実はまだダメな例がありえます。次のようなケースです。

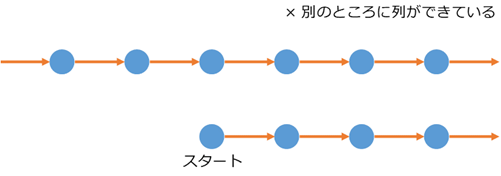
これは、「どこからともなく列ができている」という状況です。スタートもあって、次へ次へと進んではいけるんだけど、並列して別のところにも列があるというケースです。他のところに列ができているケースがあるとは盲点でしたね。

このようなイヤな構造の例を作るには、高校範囲の言葉を使うと、 $i$ を虚数単位として、

　$\{a+bi$ | $(a$ は0以上の整数かつ $b=0)$ または $(a$ は整数で $b=1)$ $\}$

とし、 $a+bi$ の次の数に $(a+1)+bi$ を対応させる、とすればいいです。今までの条件を全部クリアしていますが、こういうケースは除外したいですね。余分なものが入らない、最小の状態を考えたいので、そういう条件も必要でしょう。

「外部で列が発生していることもある」ケースに気づくと、ここまでに見た「場所が違ったら、次の場所同士も異なる」という条件は、実は次のようなケースも除外していることになります。

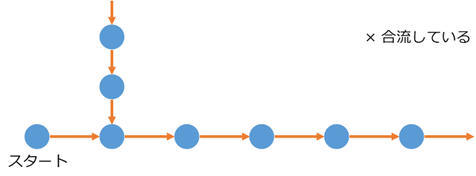
どこからともなく列ができていて、しかもそれが合流している、という構造です。これも自然数の構造とは言えなさそうなので、除外されてほしいですね。

自然数の定義（ペアノの公理）

さて、今までの内容をまとめてみます。自然数は次のような性質を持ってほしいのでした。（話の都合上、3.と4.を入れ替えています）

　1. スタートがある
　2. 次にラベルを貼る場所が1つある
　3. 今の場所が違ったら、次の場所同士も異なる
　4. 循環していない
　5. 最小の状態である

これを、もう少し数学っぽく書いてみます。もし集合 $N$ が自然数の集合だとしたら、次のような性質を持っていてほしいです。

　1. $0\in N$
　2. 各 $n\in N$ に対して、 $n^{+}\in N$ が1つ定まっている。
　3. $n\ne m$ なら $n^{+}\ne m^{+}$ が成り立つ。
　4. $n^{+}=0$ となる $n\in N$ は存在しない。
　5. $N$ は、1.～4.を満たす最小の集合である。

スタートは $0$ としています。これは自然数を構成するためのアイデアでも見たように、自然数の構成方法を考えると $0$ も自然数と考えたほうがいいからです。

1つ目と2つ目は、どういう要素が属しているか、という内容です。 $n^{+}$ は $n$ の「次の数」を表しています。つまり、この2つの条件は、最初の数があって、それぞれの数には次の数が定められている、ということを表しています。

3つ目と4つ目は、「最初の数」や「次の数」がどのような性質を持っているべきかを表しています。3つ目は「場所が違ったら、次の数同士も異なる」ことを言っていて、合流しないことを言っています。4つ目は、スタートに戻ることはないことを言っています。

5つ目は、どういう要素が属していないか（つまり、余分なものは属していない、ということ）を表しています。

最後の5つ目を言い換えれば、$N$ の部分集合が他の4つの条件を満たせば、 $N$ には余分なものがないはずなので、その部分集合は $N$ そのものだ、ということです。 $N$ の真の部分集合が他の4つの条件を満たすことはない、ともいえます。

5つ目について、もう少し考えてみます。

$S$ を $N$ の部分集合とします。 $S$ が他の4つの条件を満たすのはどういう場合でしょうか。

まず、 $0\in N$ ですが、 $S$ は部分集合なので、 $0$ が $S$ にも属しているかどうかはわかりません。なので、条件1の $0\in S$ は確かめる必要があります。

次に、条件2です。 $s\in S$ とすると、これは $s\in N$ でもあるので、 $N$ の要素として $s^{+}$ が1つに決まります。しかし、 $s^{+}\in S$ とは限りません。なので、条件2のうち、 $s^+\in S$ は確かめる必要があります。

一方、条件3はどうでしょうか。これは自動的に満たされる内容です。「次の数同士が異なる」というのは、 $S$ で考えても成り立ちます。全体で見て「合流がない」なら、部分で見ても「合流がない」はずですからね。

また、条件4も自動的に成り立ちます。 $N$ の中に $n^{+}=0$ となるものがなければ、 $S$ の中にもありません。これも、全体で見て「循環がない」なら、部分で見ても「循環がない」ことからわかるでしょう。

ということで、 $N$ の部分集合 $S$ が他の4つの条件を満たすかどうかを考えるときには、実は条件3と4は要らないんですね。 $N$ の部分集合という時点で、条件3と4は自動的に満たされるからです。

つまり、条件5とは、「部分集合 $S$ が条件1と条件2の $s^{+}\in S$ を満たしていれば、最小性から、それは $N$ そのものだよ」ということなので、条件5は、このように言い換えることができます。

　5. $N$ の部分集合 $S$ が次の(a)(b)を満たすなら、 $S=N$
　　(a) $0\in S$
　　(b) $s\in S$ ならば $s^{+}\in S$

こう書くと、なんだか見たことがあるような気がしてきます。集合の言葉ではなく、命題の言葉で書き直してみると、さらに「見たことある感」が強まってきます。部分集合 $S$ を「命題 $P(n)$ が成り立つ $n$ の集合」と考えれば、次のように言い換えられます。本当はもっと正確に書くべきですが、今は雰囲気だけわかればいいです。

　5. 次の(a)(b)を満たすとすると、命題 $P(n)$ はすべての $n\in N$ で成り立つ。
　　(a) $P(0)$ が成り立つ。
　　(b) $P(k)$ が成り立つならば $P(k^{+})$ が成り立つ。

これは、高校数学で学んだ、数学的帰納法ですね（参考：【基本】数学的帰納法）。こんな形で数学的帰納法が出てくるとは驚きですね。

さて、ここまで長々と「自然数はこのような性質を持っていてほしい」と書いてきました。実は、現代では、これを逆に用いて、これ自体を自然数の定義として採用しています。ペアノという数学者が発表したので、ペアノの公理と呼ばれています。

専門書ではいきなりこの公理の内容がドンと出てきますが、それぞれの意味するところは上で書いた通りです。「自然数だったらこういう性質を持っていてほしい、こういう性質は除外したい」というものを書き出した内容になっています。

「こうやって作ったものを自然数と言う」という定義ではなくて、「こういう性質を持つものを自然数と言う」といった自由度のある定義になっています。

ただ、自由過ぎて、不安に思う人もいるかもしれません。定義に自由度があるので、いろいろな作り方が考えられます。実際、自然数を構成するためのアイデアでも2つの構成方法があることを見ました。このようなことが起こってもいいのでしょうか。それについては、自然数系の一意性で見ることにしましょう。

なお、上の5つ目の条件は、数学的帰納法の原理と呼ばれています。

このように自然数を定義した後は、 $0$ の次の数 $0^+$ に $1$ というラベルを、 $1^+$ には $2$ というラベルを、…というようにして、通常使っている自然数と同じように扱うことにします。

定義を見るとわかりますが、自然数がバラバラに定義されているのではなく、まず自然数の集合が定義されています。そして、自然数はその集合の要素だと定義されています。自然数たちの持つ関係性（最初の数から順番に数が並んでいること）が大事であることがわかります。

自然数系

専門書によって、ペアノの公理の表し方はいろいろあります。基本的には同じ内容を表しているのですが、見た目が大きく異なるものもあります。

まず、上では、「次の数」を表すために $n^{+}$ という記号を使いました。この「次の数」は、後継者(successor) や後続者、後者と呼ばれることがあります。後継者を対応させる方法には、 $n'$ と書く方法や、successor の頭文字をとって $s(n)$ や $\mathrm{suc}(n)$ という関数で表す方法もあります。この関数を後者関数と言ったりします。

「関数」という言葉を使うと、「次の数」が1つだけに決まることを暗に含めることができます（ $x$ を決めたときに $y$ がただ1つに決まるときに、「 $y$ は $x$ の関数」と呼ぶため）。また、「 $n\ne m$ ならば $n^{+}\ne m^{+}$ 」という条件、対偶をとれば「 $n^{+}=m^{+}$ ならば $n=m$ 」となりますが、これも「単射」という言葉で片付けられて楽です。

試しに、関数を使ってペアノの公理を書いてみましょう。

最初の数を $e$ とおき、次の数を対応させる方法を $\varphi$ で表しています。構造としては、同じ内容を言っているのですが、見た目は大きく異なりますね。専門書を読んで、いきなり「これが自然数の定義です」と見せられても、なかなかはじめは厳しいと思います。「数が出てこないじゃん」という気持ちになってしまうかもしれません。

ここまでの説明からもわかりますが、集合 $N$ だけが単体で大事なわけではなく、最初の数と次の数（をどう対応させるか）を合わせた3つセットが大事です。関数バージョンの定義の書き方であれば $(N,e,\varphi)$ のことですが、この3つをセットにしたものは、自然数系やペアノ系、ペアノシステムなどと呼ばれます。

「自然数系」と呼ぶときは、自然数をただ集めるだけではなく、各自然数の関係性、つまり、最初の数からはじまって、その次の数、そのまた次の数、…と続いていく関係性・構造まで込みで考えていきますよ、と示していることになります。「自然数の集合」というだけでもこのような関係性を込めていることもありますが、「自然数系」という言葉を使った方がより明示的です。

自然数の性質

ここまでの話を使って、自然数が持つ性質を証明してみましょう。

今まで扱っていた自然数を前提とすると、これは当たり前です。自分とその次の数が一致することなんてありえません。しかし、今、新しく定義した自然数の下では、これは「当たり前」ですませずに、定義から証明できる内容となっています。練習のためにやってみます。

まず、自然数のうち、 $n\ne n^{+}$ を満たす集合を $S$ としましょう。

ペアノの公理の4つ目「 $n^{+}=0$ となる $n$ は存在しない」から、 $0^{+}\ne 0$ となります。なので、 $0\in S$ です。

次に、 $s\ne s^{+}$ としましょう。このとき、ペアノの公理の3つ目「 $n\ne m$ ならば $n^{+}\ne m^{+}$ が成り立つ」から、 $s^{+}\ne (s^{+})^{+}$ となります。つまり、 $s^{+}\in S$ です。

この2つから、ペアノの公理の5つ目より、 $S=N$ が成り立ちます。つまり、すべての自然数 $n$ について、\[
n\ne n^{+} \]が成り立ちます。これで証明終わりです。

そもそも、自然数の定義を見ると、「循環する（最初の数に戻る）」「合流する（他のところに戻る）」ケースは除外していますが、「自分の次が自分」というケースは明示的には除外していません。しかし、定義にある性質を使って、こういうケースが除外されることが示せるんですね。

もう1つ、自然数の性質を見ておきます。

これも、今までの自然数を前提とすれば当たり前ですが、新しい定義で示してみます。

次のような集合 $S$ を考えます。

　$S=\{ n \in N \mid n=0 $ または $ m^{+}=n$ となる $m\in N$ がただ1つ存在する $ \}$

まず、 $0\in S$ は定義からわかります。

また、 $n\in S$ とすると、 $n^{+}$ に対して、 $m^{+}=n^{+}$ となる $m\in S$ が存在します。 $m=n$ とすればいいです。なので、このような $m$ が 1つ以上は 存在します。

しかも、ペアノの公理の3つ目の条件より、このような $m$ は 存在すれば1つしかない ことがいえます。なので、 $n^{+}\in S$ です。

よって、ペアノの公理の5つ目より、 $S=N$ が成り立ちます。これで、証明終わりです。

この定理から、 $n$ が $0$ 以外の自然数のときには、 $m^{+}=n$ となる自然数 $m$ が存在します。この $m$ のことを、 $n$ の前者ということがあります。

このように、ペアノの公理に出てくる各条件、特に、数学的帰納法の原理を使うことで、「成り立つのが当たり前」と思っていた自然数の性質がいろいろ証明できるようになります。今後も、自然数に関する性質を証明するときには、この数学的帰納法の原理が大きな役割を果たすことになります。

ペアノが意図していたもの

自然数の定義では、ペアノの公理が用いられます。しかし、これを主張したペアノはもともと自然数を定義しようと思っていたわけではありませんでした。

ペアノ自身は、「数は定義できるものではない」と考えていました。しかし、いろんな性質を導き出せる、コアな性質（ペアノはこれを原始命題と呼びました）を挙げることはできると考えていました。それが先ほどの「ペアノの公理」で述べた条件です。

今では、ペアノの意図とは離れて、これが形式的自然数の定義に用いられるようになっています。

おわりに

ここでは、自然数の定義について見てきました。現代では、自然数の満たしてほしい性質を挙げた「ペアノの公理」を使って、自然数が定義されています。

次回は、自然数系の一意性について見ていきます。