自然数の順序

自然数の加法を踏まえて、自然数の順序について見ていきます。

自然数の順序をどう定義するか

自然数の順序とは、つまり、「5は3より大きい」というようなことです。これをどうやって定めるか、を考えていきます。

ここまで見た新しい自然数の定義（参考：自然数の定義）では、「最初の数」と「次の数」を使っていました。これらをもとにして、今までに知っていた順序と整合性をとるなら、「次の数を繰り返し求めていって、後に出てくる方が大きい数だ」と定義するのが自然でしょう。例えば、5とは、3の次の次の数だから、「5は3より大きい」と定める、ということです。

ただ、「次の数を繰り返し求めていく」というのは少し面倒です。この操作をまとめて行う、自然数の加法を定義した（参考：自然数の加法）のだから、これを使うことにしましょう。つまり、 $a,b$ という2つの自然数があったときに、 $a=b+c$ と表すことができたら $a\geqq b$ だ、などとすれば、今までに定義したものを使って順序が定義できそうですね。

順序を定義するために加法を使うので、まずは加法の性質をいくつか見ることにします。そして、それを踏まえて、順序を定義し、順序に関するいろいろな性質を見ていくことにしましょう。

自然数の順序を定義するための準備

まず、自然数の加法について、次を示しましょう。

$x$ に関して、数学的帰納法の原理を使います。 $0$ でない自然数 $y$ を固定して、
　「 $x+y\ne 0$ 」
を満たす $x\in \mathbb{N}$ の集合を $S$ とします。

$x=0$ のときは $x+y=0+y=y\ne 0$ なので、 $0\in S$ となります。

次に、 $x\in S$ とします。
\begin{eqnarray} x^{+}+y &=& y+x^{+} \\[5pt] &=& (y+x)^{+} \end{eqnarray}となります（1行目は加法の交換法則）。しかし、自然数の定義（「次の数」が $0$ になることはない）から $(y+x)^{+}\ne 0$ となります。つまり、 $x^{+}+y\ne 0$ なので、 $x^{+}\in S$ が成り立ちます。

以上より、すべての自然数 $x$ に対して、 $x+y\ne 0$ が成り立つことがわかりました。 $y$ は $0$ でない自然数なら何でもいいので、
　「 $y\ne 0$ ならば、 $x+y\ne 0$ 」
が成り立つことが示せました。

---

先ほどと似ていますが、次も示します。

右辺が $0$ ではなく $x$ になっている点が異なります。

正の数を足すのだから、これが成り立つのは自然ですね。これは、自然数の定義#自然数の性質で見た、「後継者と一致するものはない」を拡張したものです。

$x+y=x$ だったとしましょう。 $x=x+0$ なので、 $x+y=x+0$ が成り立ちます。加法の簡約法則（参考：自然数の加法#自然数の加法の簡約法則）より、 $y=0$ となりますが、これは $y\ne 0$ という仮定に矛盾します。

以上より、 $y\ne 0$ ならば、 $x+y\ne x$ が成り立つことが示せました。

---

これらから、次が成り立つことがわかります。

1つ目は、先ほど示した定理(0以外の自然数を足すと値が変わる)の対偶だから成り立ちます。

2つ目を考えます。

$x+y=0$ としましょう。最初に示した定理(0以外の自然数を足すと0にはならない)の対偶を考えると、まず $y=0$ がわかります。 $x+y=x+0=x$ だから $x=0$ もわかります。よって、 $x=y=0$ が示せました。

---

これらのことから、次のことが成り立ちます。

これは、今までの言葉で言えば、「同じでなかったら、正の自然数の分だけ離れている」ということです。これが言えれば、「だからいつでも順序を決められるんですよ」とつながっていきます。

さて、まず「あるとしたら1つしかない」ことを示しましょう。

先ほどの定理(0以外の自然数を足すと値が変わる)から、(1)と(2)が同時に起こることはありません。(2)と(3)が同時に起こることもありません。

(1)と(3)が同時に起こっているとします。このとき、 $0$ でない自然数 $a,b$ があって、 $x=y+a$, $x+b=y$ が成り立つようにできます。これより、
\begin{eqnarray} x &=& y+a \\[5pt] &=& (x+b)+a \\[5pt] &=& x+(b+a) \\[5pt] \end{eqnarray}となります。しかし、 $a\ne 0$ から、 $b+a\ne 0$ です（定理(0以外の自然数を足すと0にはならない)より）し、先ほどの定理(0以外の自然数を足すと値が変わる)からこれは起こりません。

以上から、どれか2つが同時に起こることはありえない、とわかります。

次に、「どれも起こらない」がないことを示します。

---

証明に入る前に、まずはイメージを持つために、すでに知っている言葉でどういうことをやるかを見ておきます。

$x$ に関する数学的帰納法の原理を使うので、 $x$ の場合をもとに $x^{+}$ の場合を考えます。 $x\gt y$ の場合は $x^{+}\gt y$ ですし、 $x=y$ の場合も $x^{+}\gt y$ が成り立ちます。

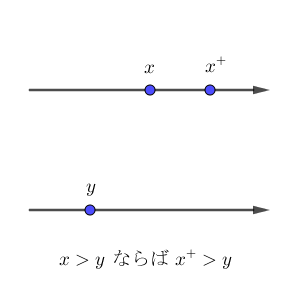
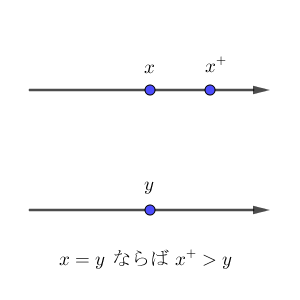
$x\lt y$ の場合は、 $x^{+}$ は $y$ に等しいこともあるし、 $y$ より小さいこともありますが、どちらにしろ、3パターンのどれかにはなります。

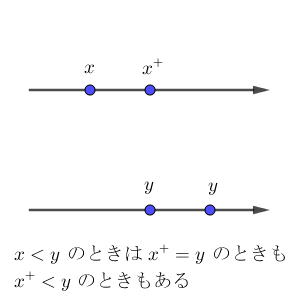
このように、3パターンのどれかになる、ということを、以下の証明では、今までに導入したものを使って書いていきます。

---

さて、「どれも起こらない」がないことの証明です。もう一度、3パターンの内容を書いておきます。

　(1) $0$ でない $z\in \mathbb{N}$ があって、 $x=y+z$ が成り立つ。
　(2) $x=y$ が成り立つ。
　(3) $0$ でない $z\in \mathbb{N}$ があって、 $x+z=y$ が成り立つ。

$y\in \mathbb{N}$ を固定し、 $x$ に関する数学的帰納法の原理を考えます。上のどれかで書ける $x\in \mathbb{N}$ の集合を $S$ とおきます。

$x=0$ のとき、 $y=0$ なら(2)が成り立ち、 $y\ne 0$ なら(3)が成り立っています（ $z=y$ とすればよい）。なので、 $0\in S$ です。

次に、 $x\in S$ としましょう。

(1)が成り立っているとすると $x=y+z$ が成り立っています。このとき、
\begin{eqnarray} x^{+} &=& (y+z)^{+} \\[5pt] &=& y+z^{+} \end{eqnarray}です。 $z^{+}\ne 0$ だから、 $x^{+}$ のときも(1)が成り立つので、 $x^{+}\in S$ です。

(2)が成り立っているとすると $x=y$ が成り立っています。このとき、
\begin{eqnarray} x^{+} &=& y^{+} \\[5pt] &=& (y+0)^{+} \\[5pt] &=& y+0^{+} \\[5pt] &=& y+1 \end{eqnarray}なので、 $z=1$ とすれば、 $x^{+}$ のときに(1)が成り立つことがわかります。 $x^{+}\in S$ です。

(3)が成り立っているとすると $x+z=y$ が成り立っています。 $z=1$ なら $x^{+}=x+1=y$ なので、(2)が成り立ちます。

以下では、 $z\ne 1$ の場合を考えます。

ここで、自然数の定義#自然数の性質の後半で見たように、 $w^{+}=z$ となる $w$ が存在します。 $0^{+}=1\ne z=w^+$ なので、 $0\ne w$ となります。

\begin{eqnarray} x^{+}+w &=& x+w^{+} \\[5pt] &=& x+z \\[5pt] &=& y \end{eqnarray}なので、 $x^{+}+w=y$ が成り立ちます。 $w\ne 0$ なので、 $x^{+}$ については(3)が成り立つことがわかります。

つまり、 $x$ について、(3)が成り立っている場合は、 $x^{+}$ は(2)か(3)のどちらか片方だけが必ず成り立つので、 $x^{+}\in S$ です。

以上から、 $x\in \mathbb{N}$ なら、(1)(2)(3)のどれかが成り立ちます。 $y$ は任意だったので、任意の $x,y\in\mathbb{N}$ に対して、(1)(2)(3)のどれかが1つだけ成り立つことが示せました。

これで証明終わりです。

自然数の順序の定義

先ほど見たことをもとにして、自然数の順序、大小関係を次のように定めることにしましょう。

これは、今までに知っている自然数の大小関係と整合性がとれています。しかも、今までに定義したものだけを使っています。「順序」を作り直したことになります。

例えば、 $5=3+2$ となるので、 $5\gt 3$ と書けます。また、 $1\lt 2$ を証明しなさいと言われたら、 $1+1=2$ だから、となります（上の定義で、 $x=1$, $z=1$, $y=2$ としています）。これが新しい定義での「順序」です。

先ほど見たように、

• $x=y+z$
• $x=y$
• $x+z=y$

のどれか1つだけが成り立つ（ $z$ は $0$ でない自然数）ので、それに応じて、大きい・等しい・小さいを決める、ということですね。1つ1つ対応しているので、逆も成り立ちます。つまり、例えば、 $x\gt y$ なら $0$ でない自然数 $z$ を使って $x=y+z$ と書けます。

さて、「 $0$ でない自然数 $z$ 」の「 $0$ でない」の部分がなくなるとどうなるでしょうか。もし、自然数 $x,y$ に対し、自然数 $z$ があって $x=y+z$ と書けていたとしましょう。 $z=0$ なら $x=y$ であり、 $z\ne 0$ なら $x\gt y$ です。このケースもよく使うので定義しておきましょう。

今までに使っていたものと整合的です。

なお、順序の定義の前に示したことから、 $x\leqq y$ と $y\leqq x$ の少なくとも一方は必ず成り立つことがわかります。

自然数の順序の反射律

この性質は、反射律(reflexivity) といいます。今までの不等号を前提にすれば当たり前ですが、新しい定義でも成り立ちます。

$x+0=x$ なので、「以下」の定義から、 $x\leqq x$ となります。定義にそって示すだけで証明終わりです。

自然数の順序の推移律

この性質は、推移律(transitivity) といいます。これも、新しい定義で考えてみましょう。

$x\leqq y$ なので、 $x+a=y$ となる自然数 $a$ が存在します。 $y\leqq z$ なので、 $y+b=z$ となる自然数 $b$ が存在します。

これより
\begin{eqnarray} z &=& y+b \\[5pt] &=& (x+a)+b \\[5pt] &=& x+(a+b) \\[5pt] \end{eqnarray}だから $x\leqq z$ が成り立ちます。

自然数の順序の反対称律

この性質は、反対称律(antisymmetry) といいます。これも、新しい定義で示してみます。

$x\leqq y$ なので、 $x+a=y$ となる自然数 $a$ が存在します。 $y\leqq x$ なので、 $y+b=x$ となる自然数 $b$ が存在します。

これより
\begin{eqnarray} x &=& y+b \\[5pt] &=& (x+a)+b \\[5pt] &=& x+(a+b) \\[5pt] \end{eqnarray}です。この記事の上の方にある、定理(加法と0)の1つ目で示したことから、 $a+b=0$ がわかり、同じところの2つ目で示したことから $a=b=0$ がわかります。よって、 $x=y+b=y+0=y$ より、 $x=y$ が示せます。

おわりに

ここでは、自然数の順序の定義をし、性質をいくつか見てきました。片方に $0$ でない自然数を足してもう片方にできるなら、前者の方が小さい、という、今まで使ってきた順序と整合性のとれている内容でした。

後半では当たり前に成り立つように感じられる性質がほとんどでした。将来、集合論を学んだときには、大小関係などを一般化した「順序」を学ぶことになりますが、そこでは、ここで見た推移律などの性質について再度見ていくことになります。