自然数の整列性と数学的帰納法

ここでは、自然数の整列性について説明し、数学的帰納法との関係について見ていきます。

最小元

自然数の順序で、自然数の順序を定義しました。このように、順序が定義された集合 $S$ があったときに、ある要素 $m\in S$ があって
　「 $s\in S$ ならば $m\leqq s$ 」
が成り立つとき、 $m$ を $S$ の最小元(least element) といいます。元（げん）と要素は同じ意味で、どちらも集合に属するもののことをいいます。

自然数全体の集合について考えると、最小元はもちろん $0$ です。

$0+x=x$ なので、順序の定義から $0\leqq x$ となることからわかります。これは、自然数の集合の最小元が $0$ であることを意味しています。

自然数の整列性

実は、全体だけではなく、任意の空でない部分集合についても最小元がある、というのが自然数の特徴です。このことを、整列性と呼びます。

もしこの性質があれば、 $S$ の最小元がとれます。そして、その要素を取り除いてまだ空集合でなければ、また最小元がとれます。これを繰り返していくと、 $S$ を小さい要素から順番に並べていくことができるわけです。

では、これを示してみましょう。

次のような集合 $T$ を考えます。

　$T=\{ n\in \mathbb{N} \mid$ 任意の $s\in S$ に対して $n\leqq s$ $\}$

これは、イメージでいうと、最小元の候補の集合です。この中に $S$ にも属しているもの があれば、それが最小元です。

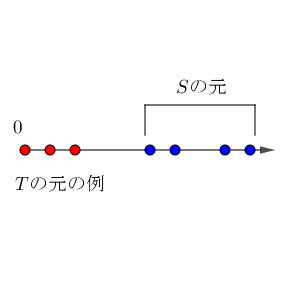
上のイメージ図からもわかりますが、 $S$ の一番左にある元が $S$ の最小元になると予想できます。そして、これは $T$ の最大元にもなっています。これを利用することを意識して、示してみましょう。

まず、先ほど示したことから、どんな $s\in S$ に対しても $0\leqq s$ なので、 $0\in T$ です。

次に、 $S$ に属する、ある $s$ をとってきます。このとき、 $s\lt s+1$ なので、 $s+1\not\in T$ となります。これから、 $T\ne \mathbb{N}$ となるので、

　(*) $m\in T$ かつ $m+1\not\in T$

となる $m\in \mathbb{N}$ が存在します（「 $m\in T$ ならば $m+1\in T$ 」がすべての $m$ に対して成り立ってしまうと、数学的帰納法の原理から $T$ は $\mathbb{N}$ に一致してしまうため）。

$m\in T$ なので、
　「任意の $x\in S$ に対して $m\leqq x$ 」
が成り立ちます。

以下では、もし $m\not\in S$ なら矛盾することを示します。 $m\not\in S$ なら、 $m=x$ となることはないので、
　「任意の $x\in S$ に対して $m\lt x$ 」
となります。

これより、ある $0$ でない自然数 $a$ があって、\[ m+a=x \]とかけます。 $a$ が $0$ でないときは、 $w^{+}=a$ となる自然数 $w$ が存在する（参考：自然数の定義#自然数の性質の後半）ので、
\begin{eqnarray} m+w^{+} &=& x \\[5pt] m+(w+1) &=& x \\[5pt] m+(1+w) &=& x \\[5pt] (m+1)+w &=& x \\[5pt] \end{eqnarray}となるから、順序の定義より

　「任意の $x\in S$ に対して $m+1\leqq x$ 」

が成り立ちます。これは $m+1\in T$ ということなので、(*)に矛盾します。

$m\not\in S$ とすると矛盾するので $m\in S$ であることがわかり、
　「任意の $x\in S$ に対して $m\leqq x$ 」
が成り立つから、 $m$ が $S$ の最小元であるとわかります。

---

自然数の場合は整列性がありますが、有理数や実数の場合などはこうはなりません。例えば、正の有理数の集合、正の実数の集合には、最小元はありません。最小元はその集合に属していないといけないので、これらのケースでは $0$ は最小元とはなりません。

自然数の整列性と数学的帰納法の原理

先ほどの証明を見直してみましょう。

　$T=\{ n\in \mathbb{N} \mid$ 任意の $s\in S$ に対して $n\leqq s$ $\}$

という集合を考えた場合、 $0\in T$ が成り立ちます。また、もし、すべての $m\in T$ について

　「 $m\in T$ ならば $m+1\in T$ 」

が成り立つなら、数学的帰納法の原理により $T=\mathbb{N}$ となりますが、 $T$ に属さない要素がある（例えば、 $S$ に属する要素より大きい自然数など）ので、これは成り立ちません。そのため、

　「 $m\in T$ かつ $m+1\not\in T$ 」

となる $m$ が存在し、結局、これが $S$ の最小元となるのでした。

この証明から、自然数の整列性は、数学的帰納法の原理から導き出されていることがわかります。ところが、実は、この逆も導けるのです。

厳密にやるなら、自然数やその順序などを、数学的帰納法の原理を使わずに整列性から定義していく必要があります（当サイトでは、数学的帰納法の原理を自然数の定義の中に入れているからです）。ただ、それをやりだすとまたすごく長くなるので、ここではそれらが定義できたとして示すことにします。なので、以下の内容は証明というよりは、証明の概要のようなものです。

$S$ の補集合 $S^c$ を考えます。つまり、

　$S^c=\{ n\in \mathbb{N} \mid$ $n\not\in S$ $\}$

です。このとき、 $S^c=\varnothing$ なら、 $S=\mathbb{N}$ が言えます。

もし、 $S^c$ が空集合でないとすると、自然数の整列性から、最小元 $m$ が存在します。特に、 $m\in S^c$ が成り立つことに注意しましょう。

(a)より、 $0$ は $S^c$ に属さないので、 $m\ne 0$ です。このとき、 $w^{+}=m$ となる $w$ が存在します。 $w\lt m$ なので、 $m$ の最小性から $w\not\in S^c$ が成り立ちます。つまり $w\in S$ となります。

(b)より $w^{+}\in S$ となりますが、これは $m\in S$ のことであり、 $m\in S^c$ に矛盾します。

以上から、 $T=\varnothing$ なので、 $S=\mathbb{N}$ が示せました。

---

これより、数学的帰納法の原理と整列性は同値だとわかります。そのため、自然数の定義を行うときには、数学的帰納法の原理ではなく、整列性から出発して考えていく方法（や専門書）もあります。

ただ、数学的帰納法の原理のほうが使い勝手がいいことや、ペアノが発表した内容には数学的帰納法の原理が採用されていたことなどから、数学的帰納法の原理の方を出発点とすることが多いです。

いろいろな数学的帰納法の形

ついでに、数学的帰納法の話をいろいろしておきましょう。

ペアノの公理の5つ目のことを数学的帰納法の原理といいます。次のような内容です。

加法を定義した今となっては、 $s^{+}$ を $s+1$ に書き換えても構いません。

これを命題の形に言い換えた、数学的帰納法もよく使います。

これは、

　$S=\{k\in \mathbb{N} \mid P(k)$ が成り立つ $\}$

という部分集合を考えれば簡単に示せます。逆に、数学的帰納法の原理を示すには、

　$P(n):$ $n\in S$

という命題を考えれば示せます。つまり、集合の形で書いても、命題の形で書いても、実質同じことというわけです。

---

数学的帰納法に似た次の形を使って証明を行うこともあります。過去のすべての結果を使うので、累積帰納法といいます。

数学的帰納法が成り立てば、累積帰納法も成り立ちます。これをまず示してみます。数学的帰納法から自然数の整列性が示せるので、それを使って示します。

累積帰納法の仮定が成り立つとして、集合 $S$ を次のように定義します。

　$S=\{n\in\mathbb{N}\mid$ $P(n)$ が成り立たない $\}$

ここで、もし $S$ が空集合でないとすると、自然数の整列性から、 $S$ には最小元 $m$ が存在します。(a)より $P(0)$ が成り立つので、 $m\ne 0$ だから、 $m=w^{+}$ を満たす $w\in\mathbb{N}$ が存在します。

このとき、最小性から、 $0\leqq k\leqq w$ を満たすすべての $k\in \mathbb{N}$ について、 $P(k)$ が成り立ちます。(b)より $P(w^{+})$ が成り立ちます。つまり、 $P(m)$ が成り立ちますが、これは $m\in S$ に矛盾します。

これから、 $S$ は空集合であり、すべての自然数 $n$ について $P(n)$ が成り立つこと、つまり、累積帰納法が成り立つことがわかります。

---

この逆も成り立ちます。つまり、累積帰納法から数学的帰納法を導けます。これも示してみましょう。

自然数 $n$ に関する命題 $P(n)$ が次の(a)(b)を満たすとします。
　(a) $P(0)$ が成り立つ。
　(b) $P(k)$ が成り立つならば $P(k+1)$ が成り立つ。

数学的帰納法の仮定が成り立つ、とするわけですね。

このとき、累積帰納法に出てくる

　$k$ 以下のすべての $m\in \mathbb{N}$ について $P(m)$ が成り立つ

について考えてみましょう。 $k$ 以下で成り立つなら、もちろん $m=k$ のときも成り立ちます。つまり、 $P(k)$ が成り立つということです。このことから、数学的帰納法の条件(b)より $P(k+1)$ が成り立ちます。つまり、累積帰納法の(b)が成り立つということです。

これと $P(0)$ が成り立つことから、累積帰納法より、すべての自然数 $n$ について $P(n)$ が成り立つことがわかります。

こうして、累積帰納法から数学的帰納法が導けました。

ここまでの内容を合わせると、次の3つ

• 数学的帰納法
• 累積帰納法
• 整列性

はすべて同値であることがわかります。

おわりに

ここでは、自然数の整列性と数学的帰納法、累積帰納法について紹介し、これらが同値であることを見てきました。数学的帰納法は今後もよく使います。集合の形ではなく、命題の形で書いたものも今後は使っていきます。