整数の乗法の定義
ここでは、整数の乗法を定義していきます。
ここまでの整数についての振り返り
整数の減法などでも見ましたが、まずは整数に関するおさらいから始めます。
自然数 $a,b$ を使って、自然数のペア $(a,b)$ を考えます。このとき、次のような集合を考えます。
$[(a,b)] = \{(c,d)\mid a+d=c+b\}$
これは、整数を $a-b$ で表そうというアイデアに基づいています。 $a-b=c-d$ なら、「 $(a,b)$ と $(c,d)$ は同じ整数を表す」と考え、各 $[(a,b)]$ を整数と呼ぶのでした。
また、2つの整数 $[(a,b)]$ と $[(c,d)]$ との和は、\[ [(a+c,b+d)] \]で定義しました。これは、 $(a-b)+(c-d)=(a+c)-(b+d)$ というアイデアによります。こうすれば、代表元によらずに和を定義することができるのでした。
整数の乗法はどう定義するのが自然か?
さて、加法を定義したので、次は乗法を定義してみましょう。これはどう定義するのがいいでしょうか。
なんとなく、 $[(a,b)]$ と $[(c,d)]$ との積は\[ [(ac,bd)] \]で定義するのが自然な気がします。が、これはうまくいきません。整数の加法の定義で見たように、このように定義すると、代表元によって、結果が変わってしまうのです。
具体例でいうと、 $[(1,3)]=[(10,12)]$ ですが、 $[(2,5)]$ との積を考えると、前者は $[(2,15)]$ となり、後者は $[(20,60)]$ となってしまいます。それぞれ、 $-13$ と $-40$ を表しており、値は一致しません。そのため、これでは そもそも定義自体ができません。
そこで、基本に立ち戻ってもう一度考えてみましょう。自然数 $a,b$ を使って、 $a-b$ で整数を表そうというのがそもそもの考えでした。ということは、整数同士の積とは、(高校までの内容を考えれば) $a-b$ と $c-d$ との積を考えることに対応します。これを計算すると
\begin{eqnarray}
(a-b)(c-d)
&=&
ac-ad-bc+bd \\[5pt]
&=&
(ac+bd)-(ad+bc)
\end{eqnarray}となります。つまり、 $[(ac,bd)]$ ではなく、$[(ac+bd, ad+bc)]$ と定義するのが自然だと考えられます。「積」と聞いただけでこの内容を思い浮かべるのは難しいですが、「そもそも何を整数だと思ってたんだっけ?」と考えていけば、この結論に到達するのは自然でしょう。
ただ、このように定義する場合も、やはり、代表元によらずに値が決められるのかは確認しないといけません。以下で見ていきましょう。
整数の乗法が代表元によらずに決まることの確認
先ほどは、 $a,b,c,d$ を自然数として、整数 $[(a,b)]$, $[(c,d)]$ の積は\[ [(ac+bd, ad+bc)] \]と定義するのが自然ではないか、という話をしました。このように定義するには、代表元によらずに値が決まることを確認しないといけません。整数の表し方によらずに値が決まることをチェックしましょう。
$a', b', c', d'$ も自然数として、 $[(a,b)]=[(a',b')]$, $[(c,d)]=[(c',d')]$ としましょう。つまり、同じ整数に対して別の表し方をしてみる、ということです。このとき、もし先ほどのように積を決めたのであれば、 $[(ac+bd, ad+bc)]$ は $[(a'c'+b'd', a'd'+b'c')]$ に一致していないといけません。これを確認してみます。
$[(a,b)]=[(a',b')]$ なので、 $a+b'=a'+b$ が成り立ちます。同様に、 $c+d'=c'+d$ も成り立ちます。左辺同士、右辺同士を掛け合わせる(これは自然数同士の掛け算です)と\[ (a+b')\cdot(c+d') = (a'+b)\cdot (c'+d) \]となります。左辺は、
\begin{eqnarray}
& &
(a+b')\cdot(c+d') \\[5pt]
&=&
a(c+d')+b'(c+d') \\[5pt]
&=&
a(c'+d)+b'(c+d') \\[5pt]
&=&
ac'+ad+b'c+b'd' \\[5pt]
\end{eqnarray}と変形できます。一方、右辺は
\begin{eqnarray}
& &
(a'+b)\cdot(c'+d) \\[5pt]
&=&
a'(c'+d)+b(c'+d) \\[5pt]
&=&
a'(c+d')+b(c'+d) \\[5pt]
&=&
a'c+a'd'+bc'+bd \\[5pt]
\end{eqnarray}と変形できます。この両辺に $a'c'+bc$ を加えると、左辺は\[ ac'+ad+b'c+b'd'+a'c'+bc \]となる一方、右辺は
\begin{eqnarray}
& &
a'c+a'd'+bc'+bd+a'c'+bc \\[5pt]
&=&
(a'+b)c+a'd'+(a'+b)c'+bd \\[5pt]
&=&
(a+b')c+a'd'+(a+b')c'+bd \\[5pt]
&=&
ac+b'c+a'd'+ac'+b'c'+bd
\end{eqnarray}が成り立ちます。この両辺から、 $b'c+ac'$ を取り除き(簡約法則)、両辺を入れ替えると
\begin{eqnarray}
ac+a'd'+b'c'+bd &=& ad+b'd'+a'c'+bc \\[5pt]
(ac+bd)+(a'd'+b'c') &=& (a'c'+b'd')+(ad+bc)
\end{eqnarray}となるので、\[ [(ac+bd,ad+bc)]=[(a'c'+b'd',a'd'+b'c')] \]となることが示せました。
つまり、 $[(a,b)]$, $[(c,d)]$ の積を、 $[(ac+bd,ad+bc)]$ で定義すれば、代表元によらずに、積を一つに決めることができる、ということです。
複雑な式変形をしているように見えますが、示したいことが決まっているので、それに向けて使えるものを使っているだけです。手を動かしてやってみると、文字が多いだけで、特に大変なことをしているわけじゃないと感じるでしょう。
整数の乗法の定義
先ほどのチェックにより、整数の乗法を次のように定義します。
\begin{eqnarray} & & [(a,b)]\cdot [(c,d)] \\[5pt] &=& [(ac+bd,ad+bc)] \end{eqnarray}また、この計算結果を積という。
なお、整数の場合も、 $x\cdot y$ のことを $x\times y$ や $xy$ とも書きます。
例えば、 $(-2)\times 3$ を計算してみましょう。この2つの整数を $[(5,7)]$, $[(4,1)]$ と表せば(別のペアで表しても構いません)、定義通りに計算すると
\begin{eqnarray}
& &
[(5\cdot 4+7\cdot 1, 5\cdot 1+7\cdot 4)] \\[5pt]
&=&
[(27,33)] \\[5pt]
&=&
[(0,6)]
\end{eqnarray}なので、 $-6$ だとわかります。高校までで見た計算と合致しています。
和の場合は、代表元によって答えが変わらないことは簡単に想像できますが、積の場合は、式が少し複雑なので、代表元によって答えが変わらないことは少し不思議に感じるかもしれません。
中学に入ってすぐに習うことで、なかなか受け入れにくい内容の一つに、「マイナス×マイナスがプラスになる」というものがあります。これもこの定義を使えば
\begin{eqnarray}
& &
[(0,1)]\times[(0,1)] \\[5pt]
&=&
[(0\cdot 0+1\cdot1, 0\cdot 1+1\cdot0)] \\[5pt]
&=&
[(1, 0)] \\[5pt]
\end{eqnarray}なので、 $(-1)\times(-1)=1$ だと証明できます。厳密に示すのであれば、自然数の定義から始まってここまでの流れを説明することになります。が、おそらく、悩める中学生が求めていたものではないでしょう。
自然数の乗法と整数の乗法
自然数の整数への埋め込みでも見たように、自然数 $n$ と 整数 $[(n,0)]$ は同一視できるのでした。
これに従うと、2つの自然数 $a,b$ は、それぞれ $[(a,0)]$, $[(b,0)]$ と同一視できます。また、前者同士の積は $ab$ であり、後者同士の積は $[(ab+0,0+0)]=[(ab,0)]$ です。つまり、積同士も対応することがわかります。
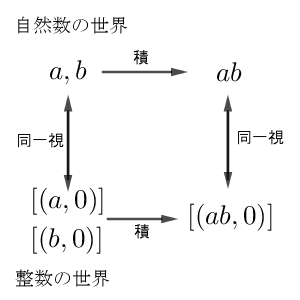
これは、元だけでなく、乗法の構造も対応している と考えられます。言い換えると、整数の乗法は、自然数の乗法を拡張したものになっている、とも言えます。
おわりに
ここでは、整数の乗法の定義について見てきました。加法のときとは違い、少し直感的ではない式を使って定義しました。意味を考えると自然ですが、何も知らない状態で見るとよくわからないでしょう。
整数の乗法がwell-definedであることも確かめました。これにより、乗法が定義できることがわかります。この定義を用いて、次では乗法の性質>を見ていきます。





