【基本】放物線で囲まれた部分の面積を和の極限で求める
ここでは、放物線で囲まれた部分の面積を、積分ではなく和の極限で求める方法を見ていきます。
放物線で囲まれた部分の面積を和の極限で求める
【基本】x軸とで囲まれた部分の面積と積分で見たように、定積分によって面積が求められるのでした。ただ、これで本当に面積が求められているのだろうか、と疑問に思う人もいるかもしれません。なにしろ、今までに扱ってきた面積とはまるで違う求め方ですからね。
定積分で面積が求められる理由は、上のリンク先にも書いていますが、少し難しいです。

$x$ を少し変化させた場合に、面積の変化幅を $x$ の変化幅で割って、 $x$ の変化幅を $0$ に近づけていくと、元の関数に戻る、だから、面積は積分で求められるんだ、という流れなのですが、ここでは、別の方法で考えてみることにしましょう。
$y=x^2$ と $x=1$, $x$ 軸で囲まれた部分の面積について考えてみましょう。
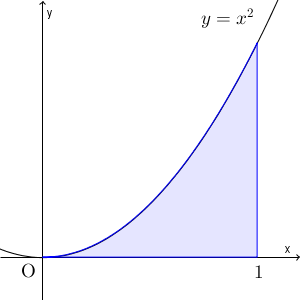
今まで計算してきた通り、これは、定積分を使って\[ \int_0^1 x^2 dx=\dfrac{1}{3} \]と求められます。ここで、もし、定積分で求める方法を知らなかったら、どうすればいいかを考えてみましょう。
過去に面積を求めた場面を思い出すと、三角形とか四角形とか円の面積は求めてきましたが、放物線で囲まれた部分は求めてませんでしたね。今まで使ってきた道具でなんとかできないかを考えてみます。単純に考えれば、今考えている部分を縦に切っていき、長方形を使って近似する方法を思いつく人もいるでしょう。
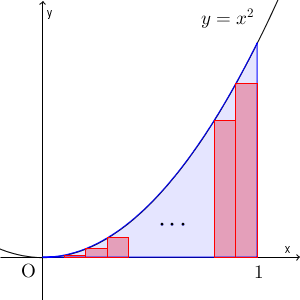
上のように、区間 $[0,1]$ を $n$ 等分して、内側に長方形をかいてみます。左上の頂点が、 $y=x^2$ 上に来るようにします。放物線の面積は、この長方形たちの面積以上になることがわかります。 $k$ を $1\leqq k\leqq n$ を満たす整数としましょう。 $\dfrac{k-1}{n}\leqq x\leqq \dfrac{k}{n}$ の間にある長方形は、横の長さが $\dfrac{1}{n}$ で、縦の長さは $\left(\dfrac{k-1}{n}\right)^2$ ですね。なので、長方形の面積の合計は
\begin{eqnarray}
& &
\dfrac{1}{n} \left\{\left(\frac{0}{n}\right)^2+\left(\frac{1}{n}\right)^2+\left(\frac{2}{n}\right)^2+\cdots +\left(\frac{n-1}{n}\right)^2\right\} \\[5pt]
&=&
\dfrac{1}{n^3} \{1^2+2^2+\cdots+(n-1)^2\} \\[5pt]
&=&
\dfrac{1}{n^3}\cdot\frac{1}{6}(n-1)n\{2(n-1)+1\} \\[5pt]
&=&
\dfrac{(n-1)(2n-1)}{6n^2} \\[5pt]
&=&
\frac{1}{6} \left(1-\frac{1}{n}\right)\left(2-\frac{1}{n}\right) \\[5pt]
\end{eqnarray}となります。途中で、【基本】和の公式(2乗の和)で見た、2乗の和の公式を使っています。上の計算から、長方形をもっと細く切っていくと、長方形の面積の合計は\[ \dfrac{1}{6}\cdot 1\cdot 2=\frac{1}{3} \]に収束することがわかります。この答えは、定積分で求めた答えと同じですね。
上の図では、長方形を内側に書きましたが、下のように外側にもかいてみましょう。
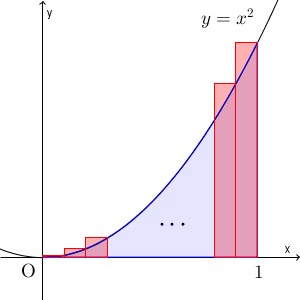
今度は、長方形の右上にある頂点が、 $y=x^2$ 上に来るようにします。こうすると、長方形の面積の合計は
\begin{eqnarray}
& &
\dfrac{1}{n} \left\{\left(\frac{1}{n}\right)^2+\left(\frac{2}{n}\right)^2+\left(\frac{3}{n}\right)^2+\cdots +\left(\frac{n}{n}\right)^2\right\} \\[5pt]
&=&
\dfrac{1}{n^3}\{1^2+2^2+\cdots+n^2\} \\[5pt]
&=&
\dfrac{(n+1)(2n+1)}{6n^2} \\[5pt]
&=&
\frac{1}{6} \left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right) \\[5pt]
\end{eqnarray}となり、 $n\to\infty$ とすると、やはり $\dfrac{1}{3}$ に収束することがわかります。
ここでは、区間を $n$ 等分して、長方形の左上の頂点、もしくは、右上の頂点が $y=x^2$ 上に来るようにして、長方形の面積で近似する、という方法で、面積を求めてみました。近似していく様子を、動画で見てみましょう。
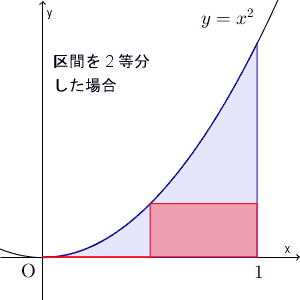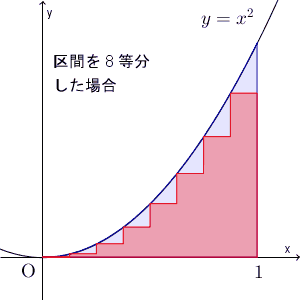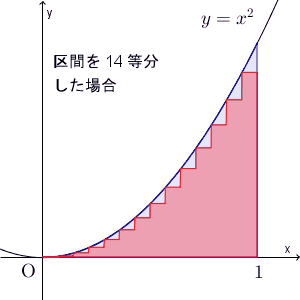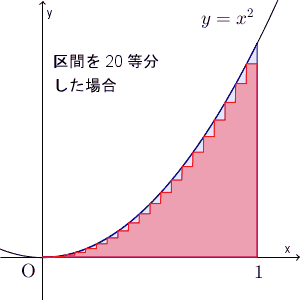
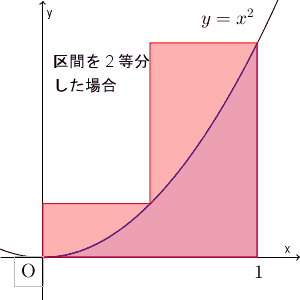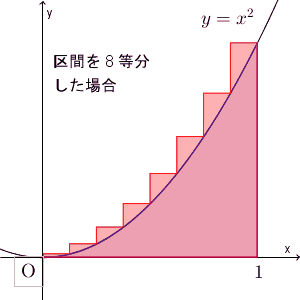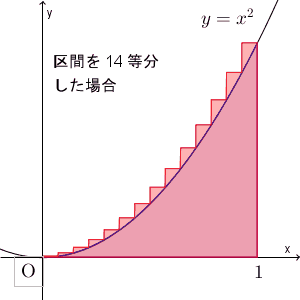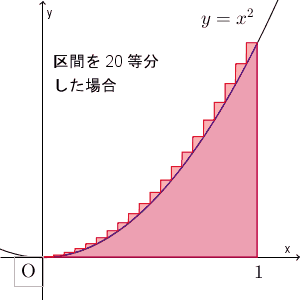
区間を細かく刻んでいくことで、近似できる様子がわかりますね。ここでは放物線のときを考えましたが、このことは一般的な連続関数に対しても成り立ちます。
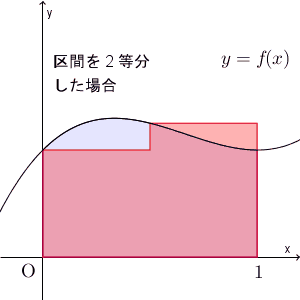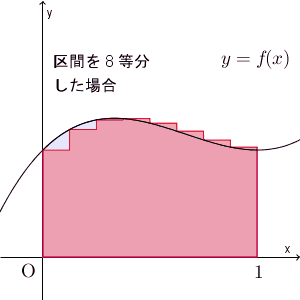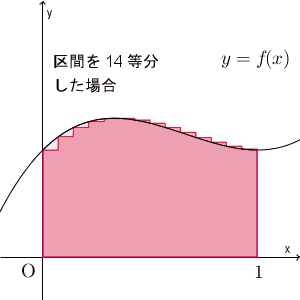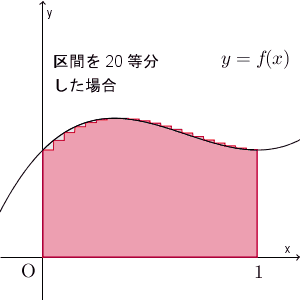
一般の場合には、別の機会に見ていきます。
おわりに
ここでは、放物線と直線で囲まれた部分の面積を、極限を使って求めてみました。縦に切って長方形で近似していく様子をイメージしましょう。





