【基本】区分求積法を使って和の極限を求める
ここでは、区分求積法を用いて、和の極限を計算する問題を見ていきます。
区分求積法を使って和の極限を求める
角の異なる $\sin$ を直接足すことは厳しそうです。なので、和の部分をきれいにまとめて簡単な式にするのは難しいです。このように、和そのものがうまく計算できない場合に、区分求積法が使える場合があります。
区分求積法とは、【基本】区分求積法の後半で見た通り、次の関係式を利用する方法です。\[ \int_0^1 f(x)dx=\lim_{n\to\infty} \frac{1}{n}\sum_{k=1}^n f\left(\frac{k}{n}\right) \]今回は、 $0$ から $1$ までの積分の方を使います。
この式と今考えている式を見比べると、似ているところが2か所あります。一つは、 $\dfrac{1}{n}$ があるところ。もう一つが、 $\sin \pi x$ に対して $x=\dfrac{k}{n}$ として $k$ を動かしたものの和になっていることです。今考えている式を、区分求積法に出てくる式にあわせて変形すると、次のようになります。
\begin{eqnarray}
& &
\lim_{n\to\infty}\frac{1}{n} \left(\sin\frac{\pi}{n}+\sin\frac{2\pi}{n}+\cdots+\sin\frac{n\pi}{n}\right) \\[5pt]
&=&
\lim_{n\to\infty}\frac{1}{n} \sum_{k=1}^n \sin\frac{k\pi}{n} \\[5pt]
\end{eqnarray}上の区分求積法の式で、 $f(x)=\sin \pi x$ としたものとなっているので、これをさらに変形すると、
\begin{eqnarray}
& &
\int_0^1 \sin \pi x dx \\[5pt]
&=&
\Big[ \frac{-\cos \pi x}{\pi} \Big]_0^1 \\[5pt]
&=&
\frac{2}{\pi}
\end{eqnarray}となることがわかります。
ここで見た、区分求積法を使って和の極限を求める様子を、図で見るとどうなるか考えてみましょう。 $y=\sin \pi x$ の $0\leqq x\leqq 1$ の区間を考えます。この区間を $n$ 等分してみましょう。
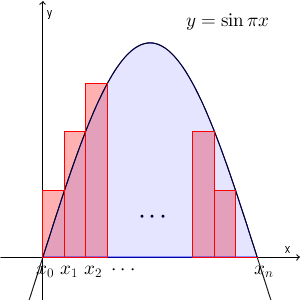
このとき、極限の式にある項 $\dfrac{1}{n}\sin\dfrac{k\pi}{n}$ は、横が $\dfrac{1}{n}$ で、縦が $\sin\dfrac{k\pi}{n}$ の長方形の面積と考えることができます。
なので、 $\lim$ の後の式は、これらの長方形の面積の和を表していて、 $n\to\infty$ と近づけていくと、次のようになります。
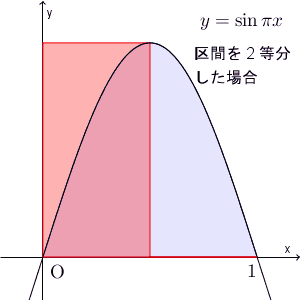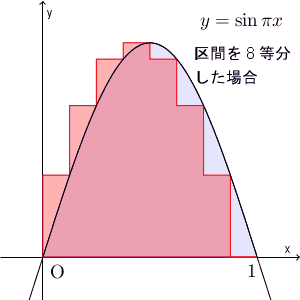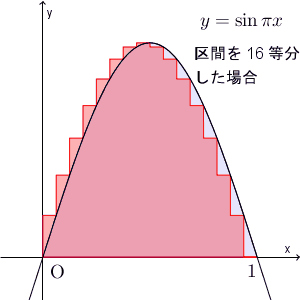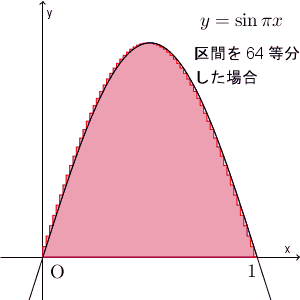
こうして、極限値は\[ \int_0^1 \sin \pi x dx \]となることがわかります。
この話は、【基本】区分求積法で見た内容を、具体的な関数で考えていることになっています。
区分求積法は、いつ使うかがわかりにくいですが、 $\dfrac{k}{n}$ を含む和の極限が出てきたときには、使う場面が多いです。そもそも和が求められない場合で、「項がどんどん増え、各項が $0$ に収束する」場合によく使われます。
おわりに
ここでは、区分求積法を使って和の極限を求める問題を見ました。普通に計算しようとしてもまったく手が出せない問題でも、区分求積法を使えばあっさり解けてしまうことがあります。練習しないとなかなか使えないので、いくつか問題を解いて練習しましょう。





