【基本】定積分を使って不等式を示す

🕒 2018/12/28 🔄 2023/05/01

ここでは、積分を使って、不等式が示せる例を見ていきます。

📘 目次

定積分と不等式と和

【基本】放物線で囲まれた部分の面積を和の極限で求めるで、 $y=x^2$ と $x=1$, $x$ 軸で囲まれた部分（下の図の青い部分）の面積は、下の図の赤い部分の長方形の面積の和より大きくなることを見ました。

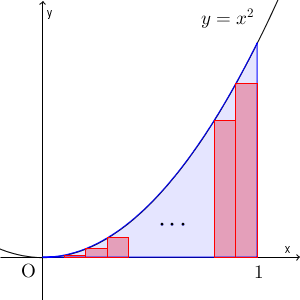
また、次のような長方形の面積の和より小さくなることも見ました。

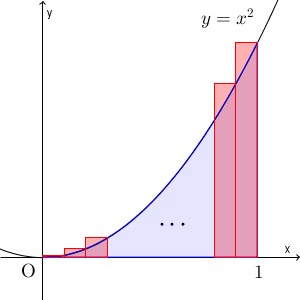
これらから、この青い部分の面積は、\[ \dfrac{1}{n} \left( \frac{0^2}{n^2}+\frac{1^2}{n^2}+\frac{2^2}{n^2}+\cdots +\frac{(n-1)^2}{n^2} \right) \]よりは大きく、\[ \dfrac{1}{n} \left( \frac{1^2}{n^2}+\frac{2^2}{n^2}+\frac{3^2}{n^2}+\cdots +\frac{n^2}{n^2} \right) \]よりは小さいことがわかります。これは、 $n$ が正の整数ならどんな時でも成り立ちます。

そして、この青い部分の面積は、\[ \int_0^1 x^2 dx = \frac{1}{3} \]となるのでしたね。

上のリンク先では、面積を求めようとしてこれらの式が出てきましたが、これらを、不等式を示すための手段として使う方法があります。

以下では、 $y=\dfrac{1}{x}$ の $1\leqq x\leqq n+1$ の範囲に対して、考えてみましょう。上の図のように、長方形も追加してみます。

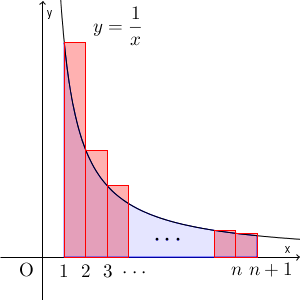
$(k,0)$, $(k+1,0)$, $\left(k+1,\dfrac{1}{k}\right)$, $\left(k,\dfrac{1}{k}\right)$ の4点を頂点とする長方形を考えます。この長方形の面積は、 $\dfrac{1}{k}$ となりますね。また、上の図からもわかる通り、これらの長方形の面積の和は、次の定積分の値（青い部分の面積）よりも大きくなることがわかります。\[ \int_1^{n+1} \dfrac{1}{x}dx \]長方形を合わせた領域の中に、「 $y=\dfrac{1}{x}$, $x=1$, $x=n+1$, $x$ 軸で囲まれた領域」がすっぽり入ってしまうからですね。

この定積分の値は、次のように計算できます。\[ \int_1^{n+1} \dfrac{1}{x}dx=\Big[ \log x \Big]_1^{n+1}=\log(n+1) \]よって、次の不等式が成り立つことがわかります。\[ 1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}\gt \log(n+1) \]この左辺を、簡単な式でまとめることはできません。なので、この不等式を直接示すことは難しいです。しかし、 $y=\dfrac{1}{x}$ を利用して作った長方形の面積と、その内側にある領域の面積とを比較することで、示すことができるんですね。このように、定積分は、不等式の証明に使われることもあります。

なお、上の不等式の右辺は、 $n\to\infty$ のときに正の無限大に発散するので、左辺も正の無限大に発散します。左辺の和は、「足しているものが小さくなっていくから、和は収束する」と勘違いする人もいるかもしれませんが、上のようにして、積分を使って発散することが示せます。

定積分と不等式

上で見た内容で基礎となっているのは、区間 $[a,b]$ で $f(x)\geqq 0$ なら、 $y=f(x)$, $x=a$, $x=b$, $x$ 軸で囲まれた部分の面積も0以上であることです。関数のグラフが $x$ 軸より上にあるなら、面積は正だ、というのは当然成り立つ話です。もう少し一般的に書くと、次のようになります。

定積分と不等式

区間 $[a,b]$ で連続な関数 $f(x),g(x)$ が、この区間で $f(x)\geqq g(x)$ を満たすとする。このとき、\[ \int_a^b f(x)dx \geqq \int_a^b g(x)dx \]が成り立つ。また、等号は $f(x)=g(x)$ がつねに成り立つときに限る。

$f(x)-g(x)$ を考えれば、先ほどと同じように考えることができます。

これは、内容だけを考えれば当然だと思えますが、具体的な式で考えると、思いもよらない結果が得られることがあります。

例えば、 $0\leqq x \leqq 1$ の範囲では、 $1+x^2\leqq 1+x$ が成り立ちます。等号は $x=0$ のときだけです。これから、\[ \frac{1}{1+x}\leqq \frac{1}{1+x^2} \]が成り立ちます。ここで、先ほど見た内容を使い、 $0$ から $1$ まで積分すると、右辺の方が大きくなることがわかります。つまり、\[ \int_0^1 \frac{1}{1+x}dx \lt \int_0^1 \frac{1}{1+x^2}dx \]が成り立ちます。

ここで、左辺は\[ \int_0^1 \dfrac{1}{1+x}dx=\Big[ \log |1+x| \Big]_0^1=\log 2 \]となります。また、右辺は、【応用】定積分の置換積分（三角関数：tanθを使う）で見た手法を使うと、 $\dfrac{\pi}{4}$ であることがわかります。つまり、\[ \log 2 \lt \dfrac{\pi}{4} \]が示せたことになるわけです。この不等式を、定積分を使わずに示すのはすごく難しいです。 $\log$ と $\pi$ は、出所が違うので、比較しようにもなかなかいい手段がありません。定積分を使えば、このような、直接には示せない不等式が得られることがあります。