【基本】区分求積法

🕒 2018/12/26 🔄 2023/06/28

ここでは、定積分を和の極限として求める、区分求積法について見ていきます。

📘 目次

区分求積法

【基本】放物線で囲まれた部分の面積を和の極限で求めるでは、放物線で囲まれた部分の面積を、積分を使わずに、和の極限で求めたのでした。アイデアとしては、区間を縦に切って、複数の長方形の面積の和を考え、区間をどんどん細かくする、というものでした。こうすれば、考えている部分に近づいていく、という発想ですね。

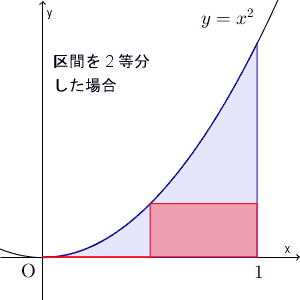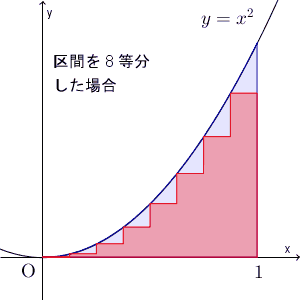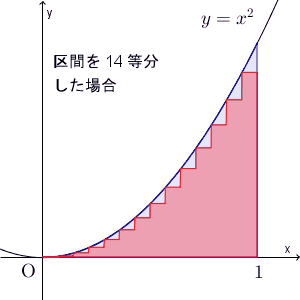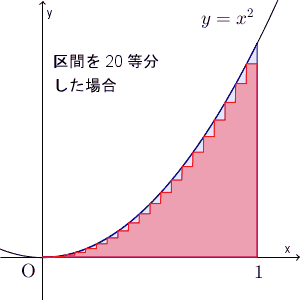
この考え方は、一般の関数の場合にも応用できます。以下で見ていきましょう。

区間 $[a,b]$ で $y=f(x)$ は0以上の値をとるとしましょう。このとき、 $y=f(x)$ と $x=a$, $x=b$, $x$ 軸で囲まれた部分の面積 $S$ について考えましょう。定積分を使って、\[ S=\int_a^b f(x) dx \]と書くこともできますが、先ほどと同じようにして考えてみましょう。

区間 $[a,b]$ を $n$ 等分して、長方形で考えてみます。また、区間の両端と分点を、左から順番に、 $x_0,x_1,\cdots,x_n$ とおくことにしましょう。もちろん、 $x_0=a$, $x_n=b$ が成り立ちます。

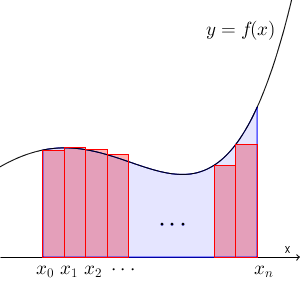
$(x_k,0)$, $(x_{k+1},0)$, $(x_{k+1},f(x_k))$, $(x_k,f(x_k))$ の4点を結んで長方形を考えます。長方形の左上の頂点が $y=f(x)$ 上に来るようにしています。この長方形の面積は\[ \frac{b-a}{n}\cdot f(x_k) \]となります。この分数の部分は、次のように置くことにしましょう。\[ \Delta x=\frac{b-a}{n} \]この $\Delta$ という記号は、微分・積分の世界でよく出てくる記号で、「デルタ」というギリシャ文字です。「少し変化させた値」を表すときに使うことが多く、 $\Delta x$ 全体で1かたまりとして扱います。 $\Delta$ と $x$ との積ではないので注意してください。この $\Delta x$ を使えば、\[ x_k=a+k\Delta x \]と書けますね。

この記号を使えば、 $n$ 個の長方形の面積の和を $S_n$ とすると、
\begin{eqnarray} S_n &=& f(x_0)\Delta x+f(x_1)\Delta x+\cdots +f(x_{n-1})\Delta x \\[5pt] &=& \sum_{k=0}^{n-1}f(x_k)\Delta x \\[5pt] \end{eqnarray}となります。

ここで、この $n$ をどんどん大きくして刻み幅をどんどん小さくしていくと、放物線のときと同様、考えている領域にどんどん近づいていくので、 $S_n\to S$ となることがわかります。式で書けば、次のようになります。\[ \int_a^b f(x)dx = \lim_{n\to\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x \]

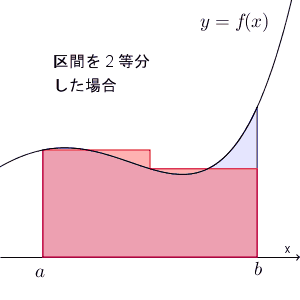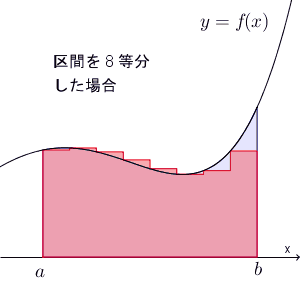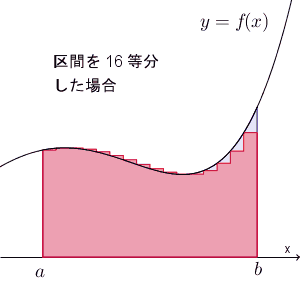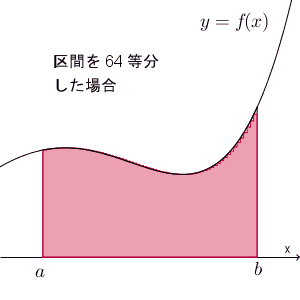
また、【基本】放物線で囲まれた部分の面積を和の極限で求めるでは、長方形の左上ではなく右上の頂点が曲線上に来る場合も、同じように収束することを見ました。今の場合も、同様で、刻み幅をどんどん小さくしていけば、 $S$ に近づいていきます。

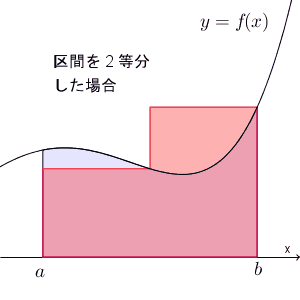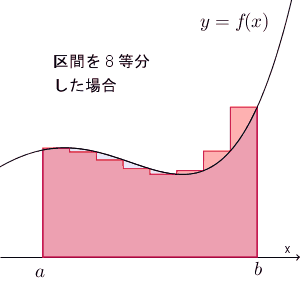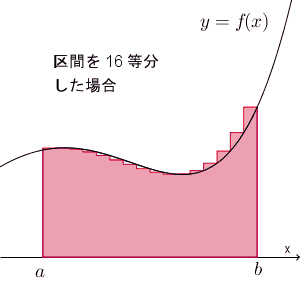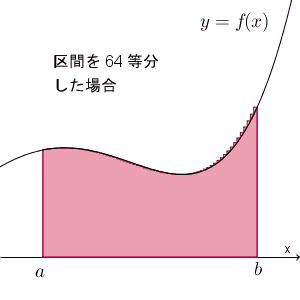
これも式で書いてみましょう。区間を $n$ 等分したとき、長方形の右上が $y=f(x)$ に来るようにしたとき、各長方形の面積の和を $T_n$ とすると
\begin{eqnarray} T_n &=& f(x_1)\Delta x+f(x_2)\Delta x+\cdots +f(x_n)\Delta x \\[5pt] &=& \sum_{k=1}^n f(x_k)\Delta x \\[5pt] \end{eqnarray}となります。順番が1つズレたことに注意しましょう。これも $S$ に収束するので、\[ \int_a^b f(x)dx = \lim_{n\to\infty}\sum_{k=1}^n f(x_k)\Delta x \]が成り立ちます。

このようにして、定積分を、和の極限を使って求める方法を、区分求積法(quadrature by parts) といいます。また、 $f(x)\geqq 0$ として話をしてきましたが、負の部分があっても、 $f(x)+M$ の積分と定数 $M$ の積分を考えることで、 $f(x)$ が連続であれば、同じ式が成り立つことがわかります。

区分求積法

$f(x)$ が、区間 $[a,b]$ で連続な関数であるとする。 $\Delta x=\dfrac{b-a}{n}$, $x_k=a+k\Delta x$ とするとき、次が成り立つ。
\begin{eqnarray} & & \int_a^b f(x)dx \\[5pt] &=& \lim_{n\to\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x \\[5pt] &=& \lim_{n\to\infty}\sum_{k=1}^n f(x_k)\Delta x \\[5pt] \end{eqnarray}

これが成り立つから何なんだ、という感じがするかもしれませんね。この区分求積法が役立つ場面を2つ紹介しましょう。

まずは、「定積分が、和の極限で書ける」ことを利用する方法です。定積分を計算するには、基本的には不定積分を求める必要があり、いつも計算できるとは限りません。しかし、和の極限で書けることがわかれば、近似値は出せるわけですね。「定積分の値をピタリと求めることはできないけど、コンピュータなどを使って計算して、近似値だけでも求めたい」という場面で使うことができます。ただ、大学入試などではこの使い方は少ないです。

もう1つは、「和の極限が、定積分で書ける」ことを利用する方法です。上の式でいうと、下から上への変形と見るわけです。直接、和の極限が計算できないような問題でも、定積分を使って表すことができることがあるんですね。このような使い方は、定期試験や大学入試でも出題されることがあります。しかも、難易度が高いです。このようにして区分求積法を使って解く問題は、別の機会に見ることにしましょう。

上で見た、区分求積法の式のうち、 $a=0$, $b=1$ のときをよく使うので、特別バージョンとして書いておきましょう。

区分求積法

$f(x)$ が、区間 $[0,1]$ で連続な関数であるとき、次が成り立つ。
\begin{eqnarray} & & \int_0^1 f(x)dx \\[5pt] &=& \lim_{n\to\infty} \frac{1}{n}\sum_{k=0}^{n-1}f\left(\frac{k}{n}\right) \\[5pt] &=& \lim_{n\to\infty} \frac{1}{n}\sum_{k=1}^n f\left(\frac{k}{n}\right) \\[5pt] \end{eqnarray}