【標準】定積分を使って不等式を示す(和を含む)
ここでは、定積分を使って不等式を示す問題を見ていきます。 $\displaystyle \sum_{k=1}^n$ を含む不等式を扱います。
定積分を使って不等式を示すその1
【基本】定積分を使って不等式を示すでも見ましたが、面積を利用し、定積分を使って不等式を示せることがあります。上のリンク先でも一部を見ましたが、次の問題を考えてみましょう。
上のリンク先では、この不等式の左側の部分を示しました。その際には、中央の式は長方形の面積を和を表している、と考えたのでした。
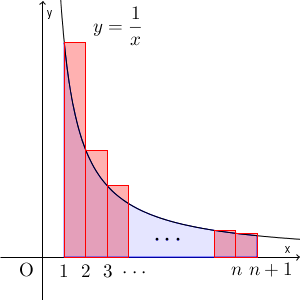
こうすると、 $y=\dfrac{1}{x}$ と $x$ 軸と $x=n+1$, $x=1$ で囲まれた部分は、 $n$ 個の長方形の領域に入るので、前者の方が面積が小さくなるんでしたね。この曲線で囲まれた部分の面積は
\begin{eqnarray}
& &
\int_1^{n+1} \frac{1}{x} dx \\[5pt]
&=&
\Big[ \log x \Big]_1^{n+1} \\[5pt]
&=&
\log (n+1)
\end{eqnarray}なので、問題の不等式にある、左側の不等号が成り立つことがわかります。
一方、右側の不等号については、より大きな領域、つまり、 $n$ 個の長方形を含む部分を考えないといけないですね。同じ高さのまま、長方形を左にずらしてみましょう。言い換えると、各長方形の左上の頂点が $y=\dfrac{1}{x}$ に来るようにしていたのを、右上の頂点が来るように変える、ということです。
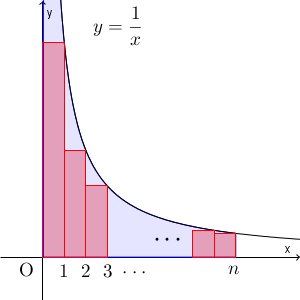
こうすれば、長方形の面積の和は、 $y=\dfrac{1}{x}$ と $x$ 軸と $x=n$, $x=0$ で囲まれた部分の面積より小さくなることがわかります。ただ、この部分の面積は計算できません。 $\dfrac{1}{x}$ を積分すると $\log x$ が出てきますが、 $x=0$ を代入することができないからです。
そこで、少し修正をしましょう。一番左端の長方形の面積は $1$ だとわかっているので、こことそれ以外で考えましょう。そうすると、 $\dfrac{1}{2}$ から $\dfrac{1}{n}$ までの和は、 $y=\dfrac{1}{x}$ と $x$ 軸と $x=n$, $x=1$ で囲まれた部分の面積より小さいことがわかります。
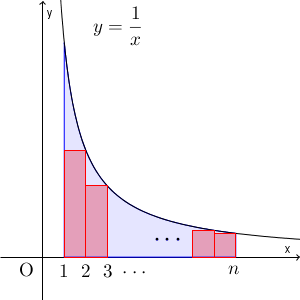
しかも、ここの部分の面積は
\begin{eqnarray}
& &
\int_1^n \frac{1}{x} dx \\[5pt]
&=&
\Big[ \log x \Big]_1^n \\[5pt]
&=&
\log n
\end{eqnarray}なので、問題の不等式にある、右側の不等号が成り立つこともわかりました。
後半部分で見たように、たくさんある長方形は、すべてをまとめて考える必要はなく、不要な部分だけを分けて考えることもできます。
定積分を使って不等式を示すその2
使う関数が違うだけで、考え方は同じです。左辺の部分が長方形の面積を表していて、右辺がそれらを含む、より大きな領域の面積を表している、と考えます。
今回は、いきなり全体を考えるのではなく、1つの長方形だけを抜き出して考えてみましょう。
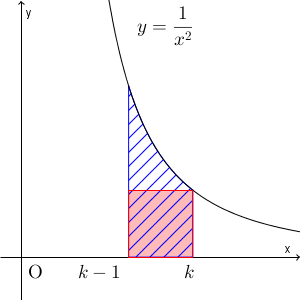
図より、 $\dfrac{1}{k^2}$ は、 $\displaystyle \int_{k-1}^{k} \dfrac{1}{x^2} dx$ より小さいことがわかります。今回も、先ほどの例題と同じように、 $0$ から積分すると計算できなくなってしまうので、 $k=2$ から $k=n$ について足し合わせて
\begin{eqnarray}
& &
\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{n^2} \\[5pt]
&\lt &
\frac{1}{1^2}+\int_1^n \dfrac{1}{x^2} dx \\[5pt]
&=&
1+\Big[ -\dfrac{1}{x} \Big]_1^n \\[5pt]
&=&
2-\dfrac{1}{n} \\[5pt]
\end{eqnarray}となり、右側の不等号が成り立つことがわかります。
s乗分の一の和について
この2つの例題から重要なことがわかります。1つ目の例題から\[ \sum_{k=1}^n \frac{1}{k}\gt \log(n+1) \]となるので、 $n\to\infty$ とすると、左辺の和は正の無限大に発散します。一方、2つ目の例題から\[ \sum_{k=1}^n \frac{1}{k^2}\lt 2-\frac{1}{n}\lt 2 \]となるので、 $n\to\infty$ とすると、左辺の和は正の無限大には発散しません。1乗か2乗かで発散する・しないが変わってくるんですね。
なお、一般的に、\[ \lim_{n\to\infty} \sum_{k=1}^n \frac{1}{k^s} \]は、 $s\gt 1$ のときは収束し、 $s\leqq 1$ のときは正の無限大に発散することが知られています。上の例題で示したような不等式を使って示すことができます。
おわりに
ここでは、定積分を使って不等式を示す問題を見ました。 $\displaystyle \sum_{k=1}^n$ を含む不等式で、和が直接計算できない場合には、積分を使って示せる場合があります。どの領域を積分すればいいか、積分した形が不等式に現れていないか、考えてみましょう。





