【基本】逆関数

🕒 2018/07/05 🔄 2023/06/22

ここでは、逆関数の定義について見ていきます。

📘 目次

逆関数

$x$ の値を決めたときに、 $y$ の値が1つだけ決まる場合、「 $y$ は $x$ の関数である」というのでした（参考：【基本】関数の復習）。

例えば、縦が $2$ の長方形があったとします。この長方形の横の長さが $x$ のとき、この長方形の周の長さが $y$ だとします。このとき、 $x$ を決めれば $y$ は次のように1つに定まります。\[ y=2x+4 \]と書くことができますね。

今の場合、逆に、周の長さから、横の長さを対応させることも可能です。周の長さを $12$ としたいなら、横の長さは $4$ とすればいいですね。周の長さから横の長さを対応させるには、周の長さを2で割って縦の長さを引けば求められます。周の長さを $y$ 、横の長さを $x$ として、\[ x=\frac{1}{2}y-2 \]となることがわかります。

$f(x)=2x+4$, $g(x)=\dfrac{1}{2}x-2$ とすると、横の長さ $x$ から周の長さ $y$ を対応させるには $y=f(x)$ とすればよく、逆に、周の長さ $y$ から横の長さ $x$ を対応させるには $x=g(y)$ とすればいいことがわかります。この2つは、対応の仕方が、ちょうど逆の関係になっていることがわかります。

このように、 $y$ が $x$ の関数で、 $y=f(x)$ と書けているときに、各 $y$ に対してもとの $x$ を $x=g(y)$ というようにしてただ1つに対応させることができる場合、 $g(x)$ は $f(x)$ の逆関数(inverse function) といいます。

$f(x)$ の逆関数を、 $f^{-1}(x)$ と表します。この $-1$ は、 $-1$ 乗のことではなく、逆であることを表しています。

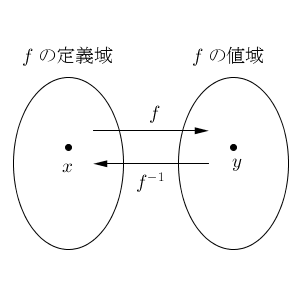
逆関数とは、ざっくりいうと、「元に戻す関数」といえます。名前の通り、「逆の」対応を示しています。このとき、対応の仕方は1通りでないといけない点に注意しましょう。逆関数も関数の1つです。なので、値が1つに決まらないと、そもそも「関数」とはいえないので、逆関数とはいいません。逆関数をもたない例は、このすぐ後で見ることにします。

逆関数がない場合

関数に対して、逆関数が常に存在するとは限りません。

例えば、 $f(x)=x^2$ を考えてみましょう。 $x=2$ なら $f(2)=4$ です。 $x=-2$ でも $f(-2)=4$ です。なので、逆の対応は1つには決まりません。 $4$ に対して、 $2$, $-2$ の2つが対応してしまうからです。

1つに決まらないということは、関数ではないということなので、逆関数が存在しない、ということです。

このように、関数によっては、逆関数が存在しない場合もあります。

一次関数の逆関数

一次関数 $f(x)=ax+b$ の逆関数を考えてみましょう( $a\ne 0$ )。

逆関数とは、 $y=f(x)$ と書けているものに対して、 $y$ から $x$ を対応させる関数を言うのでしたね。なので、 $y=f(x)$ を変形して「 $x=$ 」の形に持っていけば逆関数が求められます。
\begin{eqnarray} y &=& ax+b \\[5pt] ax &=& y-b \\[5pt] x &=& \frac{y-b}{a} \\[5pt] \end{eqnarray}これより、 $f(x)=ax+b$ の逆関数は、 $f^{-1}(x)=\dfrac{x-b}{a}$ であることがわかります。少しまぎらわしいのですが、関数をかくときには、 $x$ を変数とするのが普通です。そのため、逆関数では、 $y$ を $x$ に置き換えて書きます。

逆関数も一次関数になることがわかります。冒頭の例（長方形の周の長さの例）は、 $f(x)=2x+4$ でしたが、逆関数は $f^{-1}(x)=\dfrac{1}{2}x-2$ でしたね。たしかにこの場合も、逆関数は一次関数になっていますね。