【基本】円の接線の作図

ここでは、円の接線について説明した後に、接線の作図方法について見ていきます。

円の接線

次のように、直線が円の中心を通るとき、直線と円は2点で交わります。

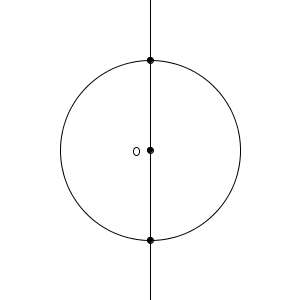
この直線を、ある方向に移動していくと、2つの交点が出会う瞬間があります。そして、それよりさらに移動すると、円は直線から離れていきます。

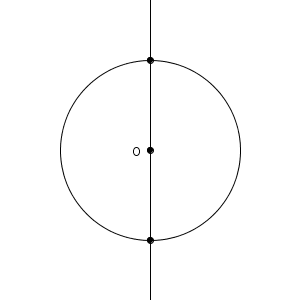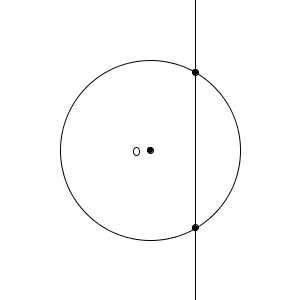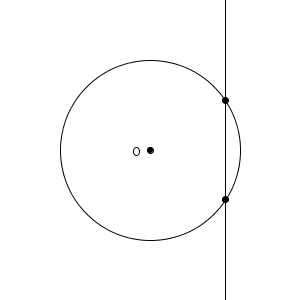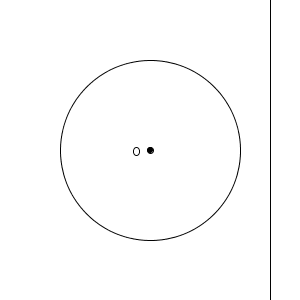
このように、直線が円の中心から離れていくと、共有点の数は、2個→1個→0個と変化していきます。このうち、円と直線の共有点が1個だけのときには、特別な名前がついています。

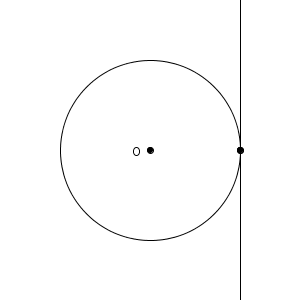
上のように、円と直線の共有点が1個のとき、「円と直線は接する(tangent) 」といいます。「直線が円に接する」ということもあります。また、この直線を円の接線(tangent line, tangent) といいます。円と接線との共有点を、接点(point of tangency) といいます。

円の接線と半径

あとで、円の接線を作図する方法を見るのですが、その前に、円の接線に関する重要な性質を見ておきます。

直線 $\ell$ が円 O と接しているとします。このとき、円の中心と接点 P とを結ぶと、この線分 OP は接線 $\ell$ と垂直に交わります。

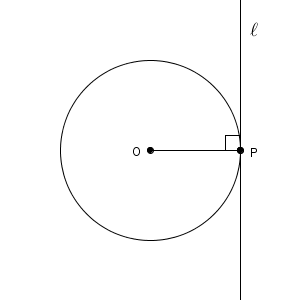
直感的には、図が OP について線対称になることからわかると思います。厳密に示すなら、次のようになります（少し難しいので、わからなければ以下の理由は飛ばしても構いません）。

点 O から直線 $\ell$ に垂線をおろし、その線と直線 $\ell$ との交点を Q としましょう。 Q が接点 P と一致することがわかったら、 OP と直線 $\ell$ とが垂直に交わることがわかるので、2点が一致することを示します。

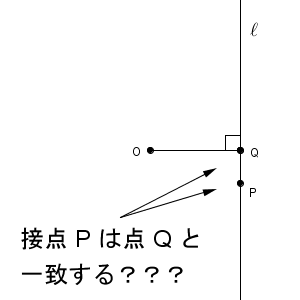
直線 $\ell$ 上の点で、点 O に一番近い点は、点 Q となります（参考：【基本】点と直線との距離と作図）。なので、 $\mathrm{ OP\geqq OQ }$ となります。

OP は円 O の半径でもあるので、もし、 $\mathrm{ OP\gt OQ }$ なら、点 Q は円 O の内側にあることになります。そうすると、直線 $\ell$ が円 O の内側の点を通ることになってしまい、円とは2点で交わることになるので、直線 $\ell$ が接線であることとつじつまが合いません。

そのため、 $\mathrm{ OP=OQ }$ となることがわかります。 P, Q は直線 $\ell$ 上の点なので、 $\mathrm{ OP=OQ }$ から、 P, Q は同じ点であることがわかり、 OP と直線 $\ell$ が垂直であることがわかります。

この性質を使って、円の接線を作図する方法を見ていきます。

円の接線の作図

次の図で、点 P で円 O と接する直線 $\ell$ を作図してみましょう。

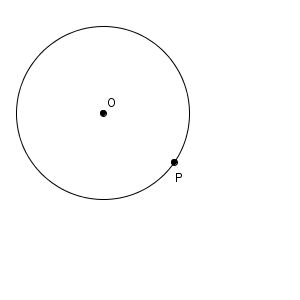
円と接点から、どうすれば接線が作図できるでしょうか。もし作図できたとしたら、次のようになるはずです。

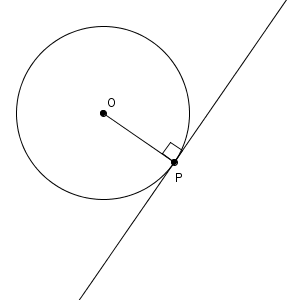
接線以外に、OP と接線が垂直で交わることもあわせてかいてみました。「垂直」や「垂線」に関する作図は、いくつかすでに見てきました。それらが使えないでしょうか。完成図を見ながら、今まで見てきた作図方法を応用できないでしょうか、考えてみましょう。

今かこうとしている接線は、点 P を通り、 OP に垂直な直線です。そのため、【基本】垂線の作図（直線上の点を通る）が利用できることがわかります。

上の図は、点 P を通り、直線 $\ell$ に垂直な直線の作図方法です。点 P を中心とした円をかき、直線との交点を中心とした円をかいて、その交点と点 P とを結べばいいのでした。

接線では、半径に垂直な直線をかけばいいので、上の作図方法を参考にすると、次のようにかけば作図できることがわかります。

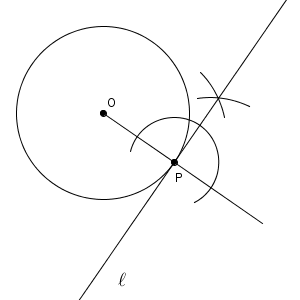
まず、 O, P を結んで、P 側に延長しておきます。それから、点 P を中心とする円をかき、直線 OP との交点を中心とする円をかいて、その交点と点 P とを結びます。こうすれば、点 P を通り、 OP に垂直な直線、つまり、点 P で円 O に接する直線がかけることになります。

ちなみに、最初に P 側に線を伸ばしていたのは、点 P を中心とする円をかいたときに、2つの交点がわかるようにするためです。

おわりに

ここでは、円の接線について見てきた後、円の接線を作図する方法を見てきました。ここでは、円と接点から接線を作図する方法を見ましたが、接線に関係する作図は他にもいくつか考えられます。他のパターンについては、別の記事で見ていくことにします。