【基本】複素数平面と2直線のなす角

ここでは、複素数平面上で、2直線のなす角の表し方について見ていきます。

複素数平面と2直線のなす角

【基本】複素数の極形式と積でも見たように、複素数の積は、拡大・縮小と回転に対応します。

例えば、 $\mathrm{ B }(\beta)$, $\mathrm{ C }(\gamma)$ に対して、原点を中心に、点 B を $r$ 倍して、$\theta$ だけ回転したときに点 C に移るとすると、\[ \gamma =r(\cos\theta+i\sin\theta)\beta \]となります。拡大・縮小と回転は、 $r(\cos\theta+i\sin\theta)$ を掛けることに対応するのでした。

回転の中心が原点ではない場合は、原点に来るように平行移動してから考えます。さらに、 $\mathrm{A}(\alpha)$ を追加しましょう。点 A を中心に、点 B を $r$ 倍して、$\theta$ だけ回転したときに、点 C に移るとしましょう。このとき、全体的に $\alpha$ を引いて、点 A が原点に来るようにすると、原点を中心に $\beta-\alpha$ を $r$ 倍して回転すれば、 $\gamma-\alpha$ に移ることがわかります。よって、\[ \gamma-\alpha =r(\cos\theta+i\sin\theta)(\beta-\alpha) \]となります。もう少し詳しいことは、【応用】複素数の積と回転に書いています。

このことを逆に使って、2直線のなす角を表すことができます。

もし、点 A, B, C がわかっている状態で、 $\angle \mathrm{ BAC }$ を求めたいとしましょう。ここでいう角は、向きを意識して、半直線 AB から反時計回りに半直線 AC を測った角のことを指すものとします。

先ほど書いた式の $\theta$ が知りたい、ということなので、両辺を $\beta-\alpha$ で割ってみましょう。\[ \frac{\gamma-\alpha}{\beta-\alpha}=r(\cos\theta+i\sin\theta) \]このようになるので、 $\theta$ は左辺の偏角であることがわかります。また、左辺の絶対値が、線分の長さの比となります。

直線のなす角を求める

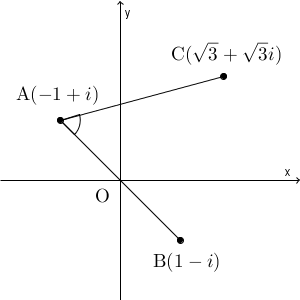
どのような複素数を掛ければいいかは、点 A が原点に来るように平行移動してから考えると、先ほど見たように\[ \frac{(\sqrt{3}+\sqrt{3}i)-(-1+i)}{(1-i)-(-1+i)} \]の偏角を求めればいいことがわかります。この式を変形していくと
\begin{eqnarray} & & \frac{(\sqrt{3}+1)+(\sqrt{3}-1)i}{2-2i} \\[5pt] &=& \frac{\{(\sqrt{3}+1)+(\sqrt{3}-1)i\}(2+2i)}{(2-2i)(2+2i)} \\[5pt] &=& \frac{4+4\sqrt{3}i}{8} \\[5pt] &=& \cos\frac{\pi}{3}+i\sin\frac{\pi}{3} \\[5pt] \end{eqnarray}となります。よって、偏角は $\dfrac{\pi}{3}$ だから、 $\angle \mathrm{ BAC }=\dfrac{\pi}{3}$ となります。

ちなみに、この計算から、絶対値が $1$ であることから、 $\mathrm{ AB=AC }$ であることがわかり、三角形 ABC が正三角形であることもわかります。

おわりに

ここでは、複素数平面上で、2直線のなす角を求めました。複素数の積が回転を表していたのですが、それを逆に使い、複素数の計算によって角度を求めたわけですね。後半では、このことを用いた問題も見ましたが、角度だけでなく、三角形の形状までわかりました。このように、複素数の計算だけでいろいろな情報が得られるので便利ですね。