共通テスト 数学II・数学B 2021年度追試 第5問 解説
【第3問~第5問から2問選択】
問題編
問題
O を原点とする座標空間に2点 $\mathrm{ A }(-1,2,0)$, $\mathrm{ B }(2,p,q)$ がある。ただし、 $q\gt 0$ とする。線分 AB の中点 C から直線 OA に引いた垂線と直線 OA の交点 D は、線分 OA を $9:1$ に内分するものとする。また、点 C から直線 OB に引いた垂線と直線 OB の交点 E は、線分 OB を $3:2$ に内分するものとする。
(1) 点 B の座標を求めよう。
$\left|\overrightarrow{ \mathrm{ OA } }\right|^2=\myBox{ア}$ である。また、 $\overrightarrow{ \mathrm{ OD } }=\dfrac{\myBox{イ} }{\myBox{ウエ} }\overrightarrow{ \mathrm{ OA } }$ であることにより、 $\overrightarrow{ \mathrm{ CD } }=\dfrac{\myBox{オ} }{\myBox{カ} }\overrightarrow{ \mathrm{ OA } }-\dfrac{\myBox{キ} }{\myBox{ク} }\overrightarrow{ \mathrm{ OB } }$ と表される。 $\overrightarrow{ \mathrm{ OA } }\perp \overrightarrow{ \mathrm{ CD } }$ から\[ \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } }=\myBox{ケ} \quad\cdots① \]である。同様に、 $\overrightarrow{ \mathrm{ CE } }$ を $\overrightarrow{ \mathrm{ OA } }$, $\overrightarrow{ \mathrm{ OB } }$ を用いて表すと、 $\overrightarrow{ \mathrm{ OB } }\perp\overrightarrow{ \mathrm{ CE } }$ から\[ \left|\overrightarrow{ \mathrm{ OB } }\right|^2=20 \quad\cdots② \]を得る。
①と②、および $q\gt 0$ から、 B の座標は $\left(2,\myBox{コ}, \sqrt{\myBox{サ} }\right)$ である。
(2) 3点 O, A, B の定める平面を $\alpha$ とし、点 $(4,4,-\sqrt{7})$ を G とする。また、 $\alpha$ 上に点 H を $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OB } }$ が成り立つようにとる。 $\overrightarrow{ \mathrm{ OH } }$ を $\overrightarrow{ \mathrm{ OA } }$, $\overrightarrow{ \mathrm{ OB } }$ を用いて表そう。
H が $\alpha$ 上にあることから、実数 $s,t$ を用いて\[ \overrightarrow{ \mathrm{ OH } }=s\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } } \]と表される。よって\[ \overrightarrow{ \mathrm{ GH } }=\myBox{シ}\overrightarrow{ \mathrm{ OG } }+s\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } } \]である。これと、 $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OA } }$ および $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OB } }$ が成り立つことから、 $s=\dfrac{\myBox{ス} }{\myBox{セ} }$, $t=\dfrac{\myBox{ソ} }{\myBox{タチ} }$ が得られる。ゆえに\[ \overrightarrow{ \mathrm{ OH } }=\dfrac{\mybox{ス} }{\mybox{セ} }\overrightarrow{ \mathrm{ OA } }+\dfrac{\mybox{ソ} }{\mybox{タチ} }\overrightarrow{ \mathrm{ OB } } \]となる。また、このことから、H は $\dBox{ツ}$ であることがわかる。
$\dbox{ツ}$ の解答群
0: 三角形 OAC の内部の点
1: 三角形 OBC の内部の点
2: 点 O, C と異なる。線分 OC 上の点
3: 三角形 OAB の周上の点
4: 三角形 OAB の内部にも周上にもない点
考え方
空間ベクトルなので図がかきにくいですが、図をかかなくても解いていくことはできます。誘導通りに計算を進めていきましょう。最後の選択問題は、係数を見て考えましょう。中線に対して H がどちらにあるかは、係数を見ただけで判断できます。
解答編
問題
O を原点とする座標空間に2点 $\mathrm{ A }(-1,2,0)$, $\mathrm{ B }(2,p,q)$ がある。ただし、 $q\gt 0$ とする。線分 AB の中点 C から直線 OA に引いた垂線と直線 OA の交点 D は、線分 OA を $9:1$ に内分するものとする。また、点 C から直線 OB に引いた垂線と直線 OB の交点 E は、線分 OB を $3:2$ に内分するものとする。
(1) 点 B の座標を求めよう。
$\left|\overrightarrow{ \mathrm{ OA } }\right|^2=\myBox{ア}$ である。また、 $\overrightarrow{ \mathrm{ OD } }=\dfrac{\myBox{イ} }{\myBox{ウエ} }\overrightarrow{ \mathrm{ OA } }$ であることにより、 $\overrightarrow{ \mathrm{ CD } }=\dfrac{\myBox{オ} }{\myBox{カ} }\overrightarrow{ \mathrm{ OA } }-\dfrac{\myBox{キ} }{\myBox{ク} }\overrightarrow{ \mathrm{ OB } }$ と表される。 $\overrightarrow{ \mathrm{ OA } }\perp \overrightarrow{ \mathrm{ CD } }$ から\[ \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } }=\myBox{ケ} \quad\cdots① \]である。同様に、 $\overrightarrow{ \mathrm{ CE } }$ を $\overrightarrow{ \mathrm{ OA } }$, $\overrightarrow{ \mathrm{ OB } }$ を用いて表すと、 $\overrightarrow{ \mathrm{ OB } }\perp\overrightarrow{ \mathrm{ CE } }$ から\[ \left|\overrightarrow{ \mathrm{ OB } }\right|^2=20 \quad\cdots② \]を得る。
①と②、および $q\gt 0$ から、 B の座標は $\left(2,\myBox{コ}, \sqrt{\myBox{サ} }\right)$ である。
解説
$\overrightarrow{ \mathrm{ OA } }$ の成分は $(-1,2,0)$ なので
\begin{eqnarray}
\left|\overrightarrow{ \mathrm{ OA } }\right|^2
&=&
(-1)^2+2^2+0^2=5
\end{eqnarray}です。また、点 D は線分 OA を $9:1$ に内分するので\[ \mathrm{ OD }=\frac{9}{10}\mathrm{ OA } \]とかけます。点 C は線分 AB の中点なので\[ \overrightarrow{ \mathrm{ OC } }=\dfrac{1}{2}\overrightarrow{ \mathrm{ OA } }+\frac{1}{2}\overrightarrow{ \mathrm{ OB } } \]とかけることから、
\begin{eqnarray}
\overrightarrow{ \mathrm{ CD } }
&=&
\overrightarrow{ \mathrm{ OD } }-\overrightarrow{ \mathrm{ OC } } \\[5pt]
&=&
\frac{9}{10}\overrightarrow{ \mathrm{ OA } }-\left(\dfrac{1}{2}\overrightarrow{ \mathrm{ OA } }+\frac{1}{2}\overrightarrow{ \mathrm{ OB } }\right) \\[5pt]
&=&
\frac{2}{5}\overrightarrow{ \mathrm{ OA } }-\frac{1}{2}\overrightarrow{ \mathrm{ OB } } \\[5pt]
\end{eqnarray}と表すことができます。
$\overrightarrow{ \mathrm{ OA } }\perp \overrightarrow{ \mathrm{ CD } }$ より、内積が $0$ だから
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ CD } } &=& 0 \\[5pt]
\overrightarrow{ \mathrm{ OA } }\cdot \left(\frac{2}{5}\overrightarrow{ \mathrm{ OA } }-\frac{1}{2}\overrightarrow{ \mathrm{ OB } }\right) &=& 0 \\[5pt]
\frac{2}{5}\left|\overrightarrow{ \mathrm{ OA } }\right|^2 -\frac{1}{2}\overrightarrow{ \mathrm{ OA } }\cdot\overrightarrow{ \mathrm{ OB } } &=& 0 \\[5pt]
2 -\frac{1}{2}\overrightarrow{ \mathrm{ OA } }\cdot\overrightarrow{ \mathrm{ OB } } &=& 0 \\[5pt]
\overrightarrow{ \mathrm{ OA } }\cdot\overrightarrow{ \mathrm{ OB } } &=& 4
\end{eqnarray}と求められます。これが①です。
また、問題文にある通り $\overrightarrow{ \mathrm{ CE } }$ についても考えます。まず、点 E は線分 OB を $3:2$ に内分しているので\[ \overrightarrow{ \mathrm{ OE } }=\frac{3}{5}\overrightarrow{ \mathrm{ OB } } \]です。これより、\[ \overrightarrow{ \mathrm{ CE } }=-\frac{1}{2}\overrightarrow{ \mathrm{ OA } }+\frac{1}{10}\overrightarrow{ \mathrm{ OB } } \]となります。また、 $\overrightarrow{ \mathrm{ OB } }\perp\overrightarrow{ \mathrm{ CE } }$ から、内積が $0$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ OB } }\cdot \left(-\frac{1}{2}\overrightarrow{ \mathrm{ OA } }+\frac{1}{10}\overrightarrow{ \mathrm{ OB } }\right) &=& 0 \\[5pt]
-\frac{1}{2}\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } } +\frac{1}{10}\left|\overrightarrow{ \mathrm{ OB } }\right|^2 &=& 0 \\[5pt]
-2 +\frac{1}{10}\left|\overrightarrow{ \mathrm{ OB } }\right|^2 &=& 0 \\[5pt]
\left|\overrightarrow{ \mathrm{ OB } }\right|^2 &=& 20 \\[5pt]
\end{eqnarray}と、問題文の②にある通りの結果が得られることがわかります。
①を、成分で表すと
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot\overrightarrow{ \mathrm{ OB } } &=& 4 \\[5pt]
(-1,2,0) \cdot (2,p,q) &=& 4 \\[5pt]
-2+2p &=& 4 \\[5pt]
p &=& 3 \\[5pt]
\end{eqnarray}と求められます。②を成分で表すと
\begin{eqnarray}
2^2+p^2+q^2 &=& 20 \\[5pt]
4+9+q^2 &=& 20 \\[5pt]
q^2 &=& 7 \\[5pt]
\end{eqnarray}となります。 $q\gt 0$ という条件があるので、 $q=\sqrt{7}$ です。こうして、 B の座標は、 $(2,3,\sqrt{7})$ と求められます。
解答
ア:5
イウエ:910
オカ:25
キク:12
ケ:4
コサ:37
解答編 つづき
(2) 3点 O, A, B の定める平面を $\alpha$ とし、点 $(4,4,-\sqrt{7})$ を G とする。また、 $\alpha$ 上に点 H を $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OB } }$ が成り立つようにとる。 $\overrightarrow{ \mathrm{ OH } }$ を $\overrightarrow{ \mathrm{ OA } }$, $\overrightarrow{ \mathrm{ OB } }$ を用いて表そう。
H が $\alpha$ 上にあることから、実数 $s,t$ を用いて\[ \overrightarrow{ \mathrm{ OH } }=s\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } } \]と表される。よって\[ \overrightarrow{ \mathrm{ GH } }=\myBox{シ}\overrightarrow{ \mathrm{ OG } }+s\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } } \]である。これと、 $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OA } }$ および $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OB } }$ が成り立つことから、 $s=\dfrac{\myBox{ス} }{\myBox{セ} }$, $t=\dfrac{\myBox{ソ} }{\myBox{タチ} }$ が得られる。ゆえに\[ \overrightarrow{ \mathrm{ OH } }=\dfrac{\mybox{ス} }{\mybox{セ} }\overrightarrow{ \mathrm{ OA } }+\dfrac{\mybox{ソ} }{\mybox{タチ} }\overrightarrow{ \mathrm{ OB } } \]となる。また、このことから、H は $\dBox{ツ}$ であることがわかる。
$\dbox{ツ}$ の解答群
0: 三角形 OAC の内部の点
1: 三角形 OBC の内部の点
2: 点 O, C と異なる。線分 OC 上の点
3: 三角形 OAB の周上の点
4: 三角形 OAB の内部にも周上にもない点
解説
点 H は、3点 O, A, B を含む平面 $\alpha$ 上にあるので、問題文にある通り、\[ \overrightarrow{ \mathrm{ OH } }=s\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } } \]と表すことができます。これより
\begin{eqnarray}
\overrightarrow{ \mathrm{ GH } }
&=&
-\overrightarrow{ \mathrm{ OG } }+\overrightarrow{ \mathrm{ OH } } \\[5pt]
&=&
-\overrightarrow{ \mathrm{ OG } }+s\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } } \\[5pt]
\end{eqnarray}となります。
$\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OA } }$ より、内積が $0$ だから
\begin{eqnarray}
\overrightarrow{ \mathrm{ GH } }\cdot\overrightarrow{ \mathrm{ OA } } &=& 0 \\[5pt]
-\overrightarrow{ \mathrm{ OG } }\cdot\overrightarrow{ \mathrm{ OA } } +s\left|\overrightarrow{ \mathrm{ OA } }\right|^2+t\overrightarrow{ \mathrm{ OB } }\cdot\overrightarrow{ \mathrm{ OA } } &=& 0 \\[5pt]
-(4,4,-\sqrt{7})\cdot(-1,2,0) +5s+4t &=& 0 \\[5pt]
5s+4t &=& 4 \\[5pt]
\end{eqnarray}が得られます。また、 $\overrightarrow{ \mathrm{ GH } }\perp\overrightarrow{ \mathrm{ OB } }$ から
\begin{eqnarray}
\overrightarrow{ \mathrm{ GH } }\cdot\overrightarrow{ \mathrm{ OB } } &=& 0 \\[5pt]
-\overrightarrow{ \mathrm{ OG } }\cdot\overrightarrow{ \mathrm{ OB } } +s\overrightarrow{ \mathrm{ OA } }\cdot\overrightarrow{ \mathrm{ OB } } +t\left|\overrightarrow{ \mathrm{ OB } }\right|^2 &=& 0 \\[5pt]
-(4,4,-\sqrt{7})\cdot(2,3,\sqrt{7}) +4s+20t &=& 0 \\[5pt]
4s+20t &=& 13 \\[5pt]
\end{eqnarray}が得られます。
これらから
\begin{eqnarray}
5(5s+4t)-(4s+20t) &=& 5\cdot 4-13 \\[5pt]
25s-4s &=& 7 \\[5pt]
s &=& \frac{1}{3} \\[5pt]
\end{eqnarray}であり、これを1つ目の式に代入して
\begin{eqnarray}
5\cdot\frac{1}{3}+4t &=& 4 \\[5pt]
4t &=& \frac{7}{3} \\[5pt]
t &=& \frac{7}{12} \\[5pt]
\end{eqnarray}となることがわかります。よって、\[ \overrightarrow{ \mathrm{ OH } }=\frac{1}{3}\overrightarrow{ \mathrm{ OA } }+\frac{7}{12}\overrightarrow{ \mathrm{ OB } } \]と表すことができます。
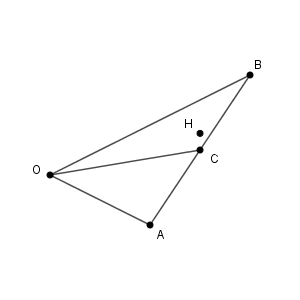
ここで、この係数の和は\[ \frac{1}{3}+\frac{7}{12}=\frac{11}{12} \]です。係数はともに正で、和は $0$ より大きく $1$ より小さいため、点 H は三角形 OAB の内部にあることがわかります。また、 $\overrightarrow{ \mathrm{ OB } }$ の係数のほうが大きいので、点 H は線分 OC に関して点 B と同じ側にあります。つまり、点 H は、三角形 OBC の内部の点であることがわかります。
長さなどはざっくりとですが、位置関係としては次の図のようになります。
解答
シ:-
スセ:13
ソタチ:712
ツ:1





