共通テスト 数学II・数学B 2021年度追試 第4問 [2] 解説
問題編
問題
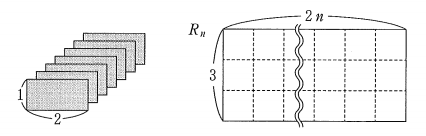
太郎さんは和室の畳を見て、畳の敷き方が何通りあるかに興味を持った。ちょうど手元にタイルがあったので、畳をタイルに置き換えて、数学的に考えることにした。
縦の長さが $1$ 、横の長さが $2$ の長方形のタイルが多数ある。それらを縦か横の向きに、隙間も重なりもなく敷き詰めるとき、その敷き詰め方をタイルの「配置」と呼ぶ。
上の図のように、縦の長さが $3$ 、横の長さが $2n$ の長方形を $R_n$ とする。 $3n$ 枚のタイルを用いた $R_n$ 内の配置の総数を $r_n$ とする。
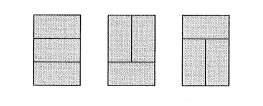
$n=1$ のときは、下の図のように $r_1=3$ である。
また、 $n=2$ のときは、下の図のように $r_2=11$ である。
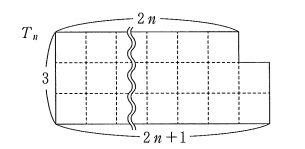
(1) 太郎さんは次のような図形 $T_n$ 内の配置を考えた。
$(3n+1)$ 枚のタイルを用いた $T_n$ 内の配置の総数を $t_n$ とする。 $n=1$ のときは、 $t_1=\myBox{ク}$ である。
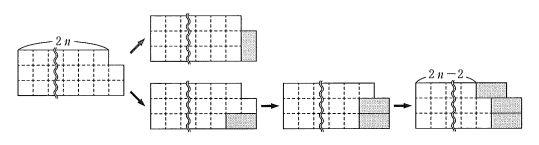
さらに、太郎さんは $T_n$ 内の配置について、右下隅のタイルに注目して次のような図をかいて考えた。
この図から、2以上の自然数 $n$ に対して\[ t_n=Ar_n+Bt_{n-1} \]が成り立つことがわかる。ただし、 $A=\myBox{ケ}$ 、 $B=\myBox{コ}$ である。
以上から、 $t_2=\myBox{サシ}$ であることがわかる。
同様に、 $R_n$ の右下隅のタイルに着目して次のような図をかいて考えた。
この図から、 $2$ 以上の自然数 $n$ に対して\[ r_n=Cr_{n-1}+Dt_{n-1} \]が成り立つことがわかる。ただし、 $C=\myBox{ス}$ 、 $D=\myBox{セ}$ である。
(2) 畳を縦の長さが $1$ 、横の長さが $2$ の長方形とみなす。縦の長さが $3$ 、横の長さが $6$ の長方形の部屋に畳を敷き詰めるとき、敷き詰め方の総数は $\myBox{ソタ}$ である。
また、縦の長さが $3$ 、横の長さが $8$ の長方形の部屋に畳を敷き詰めるとき、敷き詰め方の総数は $\myBox{チツテ}$ である。
考え方
分野でいえば、一応、数列ということになりますが、あまり数列の要素はありません。漸化式をどうやって作るか、が問題のメインです。見た目はすごく難しそうですが、よく考えるとあまり複雑なことはしていません。ヒントになっている図を読み解けるかどうかがポイントとなります。
高校数学では、漸化式を作ったあとは一般項を求める流れが多いですが、この問題では一般項を求める必要はありません。
【第3問~第5問から2問選択】
解答編
問題
太郎さんは和室の畳を見て、畳の敷き方が何通りあるかに興味を持った。ちょうど手元にタイルがあったので、畳をタイルに置き換えて、数学的に考えることにした。
縦の長さが $1$ 、横の長さが $2$ の長方形のタイルが多数ある。それらを縦か横の向きに、隙間も重なりもなく敷き詰めるとき、その敷き詰め方をタイルの「配置」と呼ぶ。
上の図のように、縦の長さが $3$ 、横の長さが $2n$ の長方形を $R_n$ とする。 $3n$ 枚のタイルを用いた $R_n$ 内の配置の総数を $r_n$ とする。
$n=1$ のときは、下の図のように $r_1=3$ である。
また、 $n=2$ のときは、下の図のように $r_2=11$ である。
解説
ここまでは敷き詰め方の例ですが、 $r_1=3$, $r_2=11$ はヒントになっています。あとの計算で使います。
解答編 つづき
(1) 太郎さんは次のような図形 $T_n$ 内の配置を考えた。
$(3n+1)$ 枚のタイルを用いた $T_n$ 内の配置の総数を $t_n$ とする。 $n=1$ のときは、 $t_1=\myBox{ク}$ である。
解説
$n=1$ のとき、 $T_1$ は次のようになります。
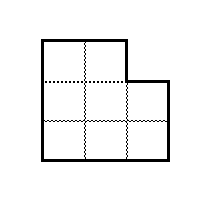
右側に突き出している部分から考えてみます。ここに横向きにタイルを置くと、他の部分は次のように配置することが確定します。
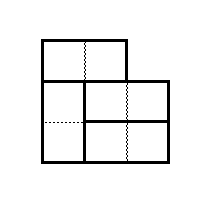
一方、この突き出した部分に縦向きにタイルを置くと、次のようになります。
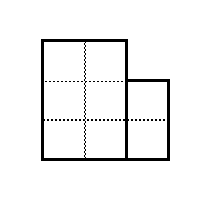
残りの部分は、 $3\times 2$ の長方形なので、先ほどの $r_1$ が使えます。 $3$ 通りです。
合わせると、突き出した部分に横向きに置いたときが $1$ 通り、縦向きに置いたときが $3$ 通りなので、\[
t_1=4 \]となります。
解答
ク:4
解答編 つづき
さらに、太郎さんは $T_n$ 内の配置について、右下隅のタイルに注目して次のような図をかいて考えた。
この図から、2以上の自然数 $n$ に対して\[ t_n=Ar_n+Bt_{n-1} \]が成り立つことがわかる。ただし、 $A=\myBox{ケ}$ 、 $B=\myBox{コ}$ である。
以上から、 $t_2=\myBox{サシ}$ であることがわかる。
解説
図をもとに考えます。
そもそも、右下の突き出した部分には、タイルを縦に置くか横に置くかしかありません。
縦に置いた場合が図の上側に対応します。このとき、残りの部分は $3\times 2n$ の長方形が残るので、この部分の敷き詰め方は $r_n$ 通りだとわかります。
一方、右下部分に横にタイルを置くと、その1段上にも横に置くしかなく、さらにその左上にも横に置くしかありません。それが、図の右下に対応しています。このとき、残りの部分は $T_{n-1}$ となっているので、この部分の敷き詰め方は $t_{n-1}$ 通りとなります。
結局、\[ t_n=r_n+t_{n-1} \]となります。
これより、
\begin{eqnarray}
t_2
&=&
r_2+t_1 \\[5pt]
&=&
11+4=15
\end{eqnarray}と求められます。 $r_2$ は冒頭の結果を使っています。
解答
ケ:1
コ:1
サシ:15
解答編 つづき
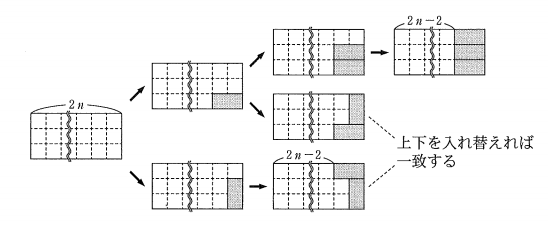
同様に、 $R_n$ の右下隅のタイルに着目して次のような図をかいて考えた。
この図から、 $2$ 以上の自然数 $n$ に対して\[ r_n=Cr_{n-1}+Dt_{n-1} \]が成り立つことがわかる。ただし、 $C=\myBox{ス}$ 、 $D=\myBox{セ}$ である。
解説
これも、図をもとに考えていきます。
右下部分に、横向きに置くか縦向きに置くか、の2通りあります。
横向きに置いた場合、さらにその上に横向きに置くと、さらにもう1つ横向きに置かなくてはいけません。それが図の1段目に対応します。この場合、残りは $3\times (2n-2)$ の長方形が残るので、敷き詰め方は $r_{n-1}$ 通りとなります。
右下に横向きに置いた後、その上に縦向きに置いた場合は、残りの部分は $T_{n-1}$ の上下逆転したものになります。なので、残りの部分の敷き詰め方は $t_{n-1}$ 通りです。
右下部分に縦に置いた場合、その上には横向きに置くしかありません。これが3段目の図に対応します。このとき、残りは、図形 $T_{n-1}$ なので、敷き詰め方は $t_{n-1}$ 通りです。
まとめると、
\begin{eqnarray}
r_n
&=&
r_{n-1}+t_{n-1}+t_{n-1} \\[5pt]
&=&
r_{n-1}+2t_{n-1}
\end{eqnarray}となります。
解答
ス:1
セ:2
解答編 つづき
(2) 畳を縦の長さが $1$ 、横の長さが $2$ の長方形とみなす。縦の長さが $3$ 、横の長さが $6$ の長方形の部屋に畳を敷き詰めるとき、敷き詰め方の総数は $\myBox{ソタ}$ である。
また、縦の長さが $3$ 、横の長さが $8$ の長方形の部屋に畳を敷き詰めるとき、敷き詰め方の総数は $\myBox{チツテ}$ である。
解説
漸化式を作ったので、後はこれに当てはめて計算するだけです。
縦の長さが $3$ で、横の長さが $6$ の長方形の場合は、 $r_3$ を計算すればいいです。
\begin{eqnarray}
r_3
&=&
r_2+2t_2 \\[5pt]
&=&
11+2\cdot 15 \\[5pt]
&=&
41 \\[5pt]
\end{eqnarray}となります。
横の長さが $8$ なら、 $r_4$ を計算すればいいので
\begin{eqnarray}
r_4
&=&
r_3+2t_3 \\[5pt]
&=&
41+2(r_3+t_2) \\[5pt]
&=&
41+2(41+15) \\[5pt]
&=&
41+2\cdot 56 \\[5pt]
&=&
153
\end{eqnarray}と求められます。
解答
ソタ:41
チツテ:153