共通テスト数学II・数学B 2021年度追試第2問 [2] 解説

🕒 2021/02/12 🔄 2022/05/16

【必答問題】

問題編

問題

　$g(x)=|x|(x+1)$ とおく。

　点 $\mathrm{ P }(-1,0)$ を通り、傾きが $c$ の直線を $\ell$ とする。 $g'(-1)=\myBox{サ}$ であるから、 $0\lt c\lt\mybox{サ}$ のとき、曲線 $y=g(x)$ と直線 $\ell$ は3点で交わる。そのうちの1点は P であり、残りの2点を点 P に近い方から順に Q, R とすると、点 Q の $x$ 座標は $\myBox{シス}$ であり、点 R の $x$ 座標は $\myBox{セ}$ である。

　また、 $0\lt c\lt \mybox{サ}$ のとき、線分 PQ と曲線 $y=g(x)$ で囲まれた図形の面積を $S$ とし、線分 QR と曲線 $y=g(x)$ で囲まれた図形の面積を $T$ とすると
\begin{eqnarray} S &=& \dfrac{\myBox{ソ}c^3+\myBox{タ}c^2-\myBox{チ}c+1}{\myBox{ツ} } \\[5pt] T &=& c^{\ \myBox{テ} } \end{eqnarray}である。

考え方

[1]とは異なり、こちらはある程度計算が必要です。 $c$ の文字が入ったまま話が進んでいきますが、図がどういう状況なのかはわかりやすいです。いきなり絶対値のついた式が出てきて驚くかもしれませんが、2つの二次関数をくっついたと考えれば、それほど難しくはないでしょう。

解答編

問題

　$g(x)=|x|(x+1)$ とおく。

　点 $\mathrm{ P }(-1,0)$ を通り、傾きが $c$ の直線を $\ell$ とする。 $g'(-1)=\myBox{サ}$ であるから、 $0\lt c\lt\mybox{サ}$ のとき、曲線 $y=g(x)$ と直線 $\ell$ は3点で交わる。そのうちの1点は P であり、残りの2点を点 P に近い方から順に Q, R とすると、点 Q の $x$ 座標は $\myBox{シス}$ であり、点 R の $x$ 座標は $\myBox{セ}$ である。

解説

$x\geqq 0$ のとき、 $g(x)=x(x+1)$ で、 $x\lt 0$ のときは $g(x)=-x(x+1)$ なので、 $y=g(x)$ のグラフは次のようになります。

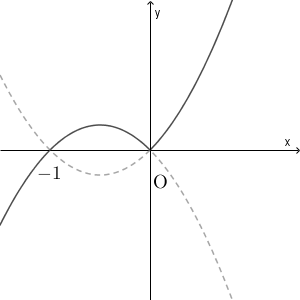
$x\lt 0$ のとき、 $g(x)=-x^2-x$ なので、 $g'(x)=-2x-1$ です。なので、 $g'(-1)=2-1=1$ です。

問題文にある通り、以下では、 $0\lt c \lt 1$ として考えます。

直線 $\ell$ の方程式は $y=c(x+1)$ です。この直線と $y=g(x)$ が $x\geqq 0$ の範囲で交わるとすると
\begin{eqnarray} c(x+1) &=& x(x+1) \\[5px] (c-x)(x+1) &=& 0 \\[5px] x &=& c, -1 \\[5px] \end{eqnarray}となり、今考えている範囲にあるものは $x=c$ のみです。また、 $x\lt 0$ の範囲では \begin{eqnarray} c(x+1) &=& -x(x+1) \\[5px] (c+x)(x+1) &=& 0 \\[5px] x &=& -c, -1 \\[5px] \end{eqnarray}となり、どちらも、今考えている範囲にあります。 P の座標が $-1$ でこれに近い方が Q なので、 Q の $x$ 座標は $-c$ で、 R の $x$ 座標は $c$ だとわかります。

解答

サ：1
シス：-c
セ：c

解答編つづき

　また、 $0\lt c\lt \mybox{サ}$ のとき、線分 PQ と曲線 $y=g(x)$ で囲まれた図形の面積を $S$ とし、線分 QR と曲線 $y=g(x)$ で囲まれた図形の面積を $T$ とすると
\begin{eqnarray} S &=& \dfrac{\myBox{ソ}c^3+\myBox{タ}c^2-\myBox{チ}c+1}{\myBox{ツ} } \\[5pt] T &=& c^{\ \myBox{テ} } \end{eqnarray}である。

解説

図は次のようになっています。

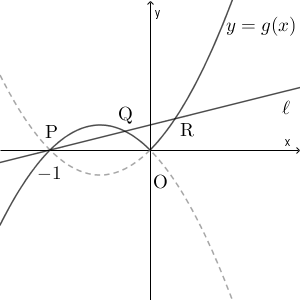
線分 PQ と曲線 $y=g(x)$ で囲まれた部分の面積は、 $y=-x^2-x$ と線分 PQ とで囲まれた部分の面積と等しいので
\begin{eqnarray} & & S \\[5pt] &=& \int_{-1}^{-c} \{(-x^2-x)-(cx+c)\} dx \\[5pt] &=& \int_{-1}^{-c} \{ -x^2-(c+1)x-c \} dx \\[5pt] &=& \left[-\dfrac{x^3}{3}-\dfrac{(c+1)x^2}{2}-cx\right]_{-1}^{-c} \\[5pt] &=& \left(-\dfrac{-c^3}{3}-\dfrac{(c+1)c^2}{2}+c^2\right) \\[5pt] & & -\left(-\dfrac{-1}{3}-\dfrac{c+1}{2}+c\right) \\[5pt] &=& \left(\dfrac{c^3}{3}-\dfrac{c^3+c^2}{2}+c^2\right) \\[5pt] & & -\left(\dfrac{c}{2}-\dfrac{1}{6}\right) \\[5pt] &=& -\dfrac{c^3}{6}+\dfrac{c^2}{2}-\dfrac{c}{2}+\dfrac{1}{6} \\[5pt] &=& \dfrac{-c^3+3c^2-3c+1}{6} \end{eqnarray}となります。

なお、これは、放物線と直線で囲まれた部分の面積なので、いわゆる $\dfrac{1}{6}$ 公式を知っている場合は、\[ \frac{(-c+1)^3}{6}=\frac{-c^3+3c^2-3c+1}{6} \]と求めることもできます。（参考：【応用】放物線と直線で囲まれた部分の面積を簡単に求める）

次に、線分 QR と曲線 $y=g(x)$ で囲まれた部分の面積を求めます。 $y=g(x)$ のグラフは $x=0$ を境に状況が変わるので、 $x=0$ の左側と右側とで分けて求めるようにします。

$x=0$ より左の部分は、今回は直線のほうが上にあるので
\begin{eqnarray} & & \int_{-c}^{0} \{(cx+c)-(-x^2-x)\} dx \\[5pt] &=& \int_{-c}^{0} \{ x^2+(c+1)x+c \} dx \\[5pt] &=& \left[\dfrac{x^3}{3}+\dfrac{(c+1)x^2}{2}+cx\right]_{-c}^{0} \\[5pt] &=& -\left(\dfrac{-c^3}{3}+\dfrac{(c+1)c^2}{2}-c^2\right) \\[5pt] &=& -\left(\dfrac{c^3}{6}-\dfrac{c^2}{2}\right) \\[5pt] &=& -\dfrac{c^3}{6}+\dfrac{c^2}{2} \end{eqnarray}と求められます。

一方、右側の部分の面積は
\begin{eqnarray} & & \int_{0}^{c} \{(cx+c)-(x^2+x)\} dx \\[5pt] &=& \int_{0}^{c} \{ -x^2+(c-1)x+c \} dx \\[5pt] &=& \left[-\dfrac{x^3}{3}+\dfrac{(c-1)x^2}{2}+cx\right]_{0}^{c} \\[5pt] &=& -\frac{c^3}{3}+\frac{(c-1)c^2}{2}+c^2 \\[5pt] &=& \dfrac{c^3}{6}+\dfrac{c^2}{2} \end{eqnarray}と求められます。

以上から、
\begin{eqnarray} T &=& \left(-\dfrac{c^3}{6}+\dfrac{c^2}{2}\right)+\left(\dfrac{c^3}{6}+\dfrac{c^2}{2}\right) \\[5pt] &=& c^2 \end{eqnarray}と求められます。