共通テスト 数学II・数学B 2021年度追試 第1問 [2] 解説
【必答問題】
問題編
問題
座標平面上の原点を中心とする半径 $1$ の円周上に3点 $\mathrm{ P }(\cos\theta,\sin\theta)$, $\mathrm{ Q }(\cos\alpha, \sin\alpha)$, $\mathrm{ R }(\cos\beta,\sin\beta)$ がある、ただし、 $0\leqq \theta\lt \alpha\lt\beta\lt 2\pi$ とする。このとき、 $s$ と $t$ を次のように定める。
\begin{eqnarray} s &=& \cos\theta+\cos\alpha+\cos\beta \\[5pt] t &=& \sin\theta+\sin\alpha+\sin\beta \\[5pt] \end{eqnarray}(1) $\triangle \mathrm{ PQR }$ が正三角形や二等辺三角形のときの $s$ と $t$ の値について考察しよう。
考察1
$\triangle \mathrm{ PQR }$ が正三角形である場合を考える。この場合、 $\alpha$, $\beta$ を $\theta$ で表すと
\begin{eqnarray} \alpha &=& \theta+\dfrac{\myBox{シ} }{3}\pi \\[5pt] \beta &=& \theta+\dfrac{\myBox{ス} }{3}\pi \end{eqnarray}であり、加法定理により \begin{eqnarray} \cos\alpha &=& \dBox{セ} \\[5pt] \sin\alpha &=& \dBox{ソ} \end{eqnarray}である。同様に、 $\cos\beta$ および $\sin\beta$ を、 $\sin\theta$ と $\cos\theta$ を用いて表すことができる。これらのことから、 $s=t=\myBox{タ}$ である。
$\dbox{セ}, \dbox{ソ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\dfrac{1}{2}\sin\theta+\dfrac{\sqrt{3} }{2}\cos\theta$
1: $\dfrac{\sqrt{3} }{2}\sin\theta+\dfrac{1}{2}\cos\theta$
2: $\dfrac{1}{2}\sin\theta-\dfrac{\sqrt{3} }{2}\cos\theta$
3: $\dfrac{\sqrt{3} }{2}\sin\theta-\dfrac{1}{2}\cos\theta$
4: $-\dfrac{1}{2}\sin\theta+\dfrac{\sqrt{3} }{2}\cos\theta$
5: $-\dfrac{\sqrt{3} }{2}\sin\theta+\dfrac{1}{2}\cos\theta$
6: $-\dfrac{1}{2}\sin\theta-\dfrac{\sqrt{3} }{2}\cos\theta$
7: $-\dfrac{\sqrt{3} }{2}\sin\theta-\dfrac{1}{2}\cos\theta$
考察2
$\triangle \mathrm{ PQR }$ が $\mathrm{ PQ=PR }$ となる二等辺三角形である場合を考える。例えば、点 P が直線 $y=x$ 上にあり、点 Q, R が直線 $y=x$ に関して対称であるときを考える。このとき、 $\theta=\dfrac{\pi}{4}$ である。また、 $\alpha$ は $\alpha\lt\dfrac{5}{4}\pi$, $\beta$ は $\dfrac{5}{4}\pi\lt\beta$ を満たし、点 Q, R の座標について、 $\sin\beta=\cos\alpha$, $\cos\beta=\sin\alpha$ が成り立つ。よって\[ s=t=\dfrac{\sqrt{\myBox{チ} }}{\myBox{ツ} }+\sin\alpha+\cos\alpha \]である。
ここで、三角関数の合成により\[ \sin\alpha+\cos\alpha=\sqrt{\myBox{テ} } \sin\left(\alpha+\dfrac{\pi}{\myBox{ト} }\right) \]である。したがって\[ \alpha=\dfrac{\myBox{ナニ} }{12}\pi, \beta=\dfrac{\myBox{ヌネ} }{12}\pi \]のとき、 $s=t=0$ である。
(2) 次に、 $s$ と $t$ の値を定めたときの $\theta$, $\alpha$, $\beta$ の関係について考察しよう。
考察3
$s=t=0$ の場合を考える。この場合、 $\sin^2\theta+\cos^2\theta=1$ により、 $\alpha$ と $\beta$ について考えると\[ \cos\alpha\cos\beta+\sin\alpha\sin\beta=\dfrac{\myBox{ノハ} }{\myBox{ヒ} } \]である。
同様に、 $\theta$ と $\alpha$ について考えると\[ \cos\theta\cos\alpha+\sin\theta\sin\alpha=\dfrac{\mybox{ノハ} }{\mybox{ヒ} } \]であるから、 $\theta$, $\alpha$, $\beta$ の範囲に注意すると\[ \beta-\alpha=\alpha-\theta=\dfrac{\myBox{フ} }{\myBox{ヘ} }\pi \]という関係が得られる。
(3) これまでの考察を振り返ると、次の 0 ~ 3 のうち、正しいものは $\dBox{ホ}$ であることがわかる。
$\dbox{ホ}$ の解答群
0: $\triangle \mathrm{ PQR }$ が正三角形ならば $s=t=0$ であり、 $s=t=0$ ならば $\triangle \mathrm{ PQR }$ は正三角形である。
1: $\triangle \mathrm{ PQR }$ が正三角形ならば $s=t=0$ であるが、 $s=t=0$ であっても $\triangle \mathrm{ PQR }$ が正三角形でない場合がある。
2: $\triangle \mathrm{ PQR }$ が正三角形であっても $s=t=0$ でない場合があるが、 $s=t=0$ ならば $\triangle \mathrm{ PQR }$ は正三角形である。
3: $\triangle \mathrm{ PQR }$ が正三角形であっても $s=t=0$ でない場合があり、 $s=t=0$ であっても $\triangle \mathrm{ PQR }$ が正三角形でない場合がある。
考え方
図形と絡めた問題です。図形の知識はほとんどなくてもできますが、あるとさらに考えやすくなるかもしれません。誘導は丁寧です。
(3)は、(2)までの内容が解けていれば選べます。ただ、(1)の後半があるせいで、逆に少し迷ってしまうかもしれません。
解答編
問題
座標平面上の原点を中心とする半径 $1$ の円周上に3点 $\mathrm{ P }(\cos\theta,\sin\theta)$, $\mathrm{ Q }(\cos\alpha, \sin\alpha)$, $\mathrm{ R }(\cos\beta,\sin\beta)$ がある、ただし、 $0\leqq \theta\lt \alpha\lt\beta\lt 2\pi$ とする。このとき、 $s$ と $t$ を次のように定める。
\begin{eqnarray} s &=& \cos\theta+\cos\alpha+\cos\beta \\[5pt] t &=& \sin\theta+\sin\alpha+\sin\beta \\[5pt] \end{eqnarray}(1) $\triangle \mathrm{ PQR }$ が正三角形や二等辺三角形のときの $s$ と $t$ の値について考察しよう。
考察1
$\triangle \mathrm{ PQR }$ が正三角形である場合を考える。この場合、 $\alpha$, $\beta$ を $\theta$ で表すと
\begin{eqnarray} \alpha &=& \theta+\dfrac{\myBox{シ} }{3}\pi \\[5pt] \beta &=& \theta+\dfrac{\myBox{ス} }{3}\pi \end{eqnarray}であり、加法定理により \begin{eqnarray} \cos\alpha &=& \dBox{セ} \\[5pt] \sin\alpha &=& \dBox{ソ} \end{eqnarray}である。同様に、 $\cos\beta$ および $\sin\beta$ を、 $\sin\theta$ と $\cos\theta$ を用いて表すことができる。これらのことから、 $s=t=\myBox{タ}$ である。
$\dbox{セ}, \dbox{ソ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\dfrac{1}{2}\sin\theta+\dfrac{\sqrt{3} }{2}\cos\theta$
1: $\dfrac{\sqrt{3} }{2}\sin\theta+\dfrac{1}{2}\cos\theta$
2: $\dfrac{1}{2}\sin\theta-\dfrac{\sqrt{3} }{2}\cos\theta$
3: $\dfrac{\sqrt{3} }{2}\sin\theta-\dfrac{1}{2}\cos\theta$
4: $-\dfrac{1}{2}\sin\theta+\dfrac{\sqrt{3} }{2}\cos\theta$
5: $-\dfrac{\sqrt{3} }{2}\sin\theta+\dfrac{1}{2}\cos\theta$
6: $-\dfrac{1}{2}\sin\theta-\dfrac{\sqrt{3} }{2}\cos\theta$
7: $-\dfrac{\sqrt{3} }{2}\sin\theta-\dfrac{1}{2}\cos\theta$
解説
$\triangle \mathrm{ PQR }$ が正三角形のときは、次のような状況になっています。
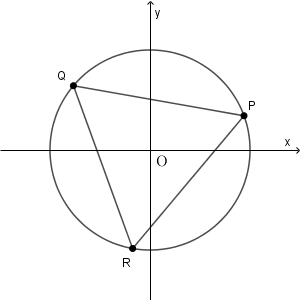
三角形 OPQ, 三角形 OQR, 三角形 ORP は互いに合同なので、\[ \alpha=\theta+\dfrac{2}{3}\pi,\ \beta=\theta+\dfrac{4}{3}\pi \]という関係式が成り立ちます。
加法定理から
\begin{eqnarray}
\cos\alpha
&=&
\cos\left(\theta+\dfrac{2}{3}\pi\right) \\[5pt]
&=&
\cos\theta\cos\frac{2}{3}\pi-\sin\theta\sin\frac{2}{3}\pi \\[5pt]
&=&
-\frac{1}{2}\cos\theta-\frac{\sqrt{3} }{2}\sin\theta \\[5pt]
&=&
-\frac{\sqrt{3} }{2}\sin\theta-\frac{1}{2}\cos\theta \\[5pt]
\end{eqnarray}となり、
\begin{eqnarray}
\sin\alpha
&=&
\sin\left(\theta+\dfrac{2}{3}\pi\right) \\[5pt]
&=&
\sin\theta\cos\frac{2}{3}\pi+\cos\theta\sin\frac{2}{3}\pi \\[5pt]
&=&
-\frac{1}{2}\sin\theta+\frac{\sqrt{3} }{2}\cos\theta \\[5pt]
\end{eqnarray}となります。
同様に
\begin{eqnarray}
\cos\beta
&=&
\cos\left(\theta+\dfrac{4}{3}\pi\right) \\[5pt]
&=&
\cos\theta\cos\frac{4}{3}\pi-\sin\theta\sin\frac{4}{3}\pi \\[5pt]
&=&
-\frac{1}{2}\cos\theta+\frac{\sqrt{3} }{2}\sin\theta \\[5pt]
\end{eqnarray}であり、
\begin{eqnarray}
\sin\beta
&=&
\sin\left(\theta+\dfrac{4}{3}\pi\right) \\[5pt]
&=&
\sin\theta\cos\frac{4}{3}\pi+\cos\theta\sin\frac{4}{3}\pi \\[5pt]
&=&
-\frac{1}{2}\sin\theta-\frac{\sqrt{3} }{2}\cos\theta \\[5pt]
\end{eqnarray}となります。
以上から
\begin{eqnarray}
s
&=&
\cos\theta + \cos\alpha + \cos\beta \\[5pt]
&=&
\cos\theta +\left(-\frac{1}{2}\cos\theta-\frac{\sqrt{3} }{2}\sin\theta\right) +\left(-\frac{1}{2}\cos\theta+\frac{\sqrt{3} }{2}\sin\theta\right) \\[5pt]
&=&
0
\end{eqnarray}となり、
\begin{eqnarray}
t
&=&
\sin\theta + \sin\alpha + \sin\beta \\[5pt]
&=&
\sin\theta +\left(-\frac{1}{2}\sin\theta+\frac{\sqrt{3} }{2}\cos\theta\right) +\left(-\frac{1}{2}\sin\theta-\frac{\sqrt{3} }{2}\cos\theta\right) \\[5pt]
&=&
0
\end{eqnarray}と求められます。
なお、図形的には、点 $\left(\dfrac{s}{3}, \dfrac{t}{3}\right)$ は三角形 PQR の重心の座標のことであり、正三角形なら重心と外心が一致することから、 $s=t=0$ になると考えることもできます。
解答
シ:2
ス:4
セ:7
ソ:4
タ:0
解答編 つづき
考察2
$\triangle \mathrm{ PQR }$ が $\mathrm{ PQ=PR }$ となる二等辺三角形である場合を考える。例えば、点 P が直線 $y=x$ 上にあり、点 Q, R が直線 $y=x$ に関して対称であるときを考える。このとき、 $\theta=\dfrac{\pi}{4}$ である。また、 $\alpha$ は $\alpha\lt\dfrac{5}{4}\pi$, $\beta$ は $\dfrac{5}{4}\pi\lt\beta$ を満たし、点 Q, R の座標について、 $\sin\beta=\cos\alpha$, $\cos\beta=\sin\alpha$ が成り立つ。よって\[ s=t=\dfrac{\sqrt{\myBox{チ} }}{\myBox{ツ} }+\sin\alpha+\cos\alpha \]である。
ここで、三角関数の合成により\[ \sin\alpha+\cos\alpha=\sqrt{\myBox{テ} } \sin\left(\alpha+\dfrac{\pi}{\myBox{ト} }\right) \]である。したがって\[ \alpha=\dfrac{\myBox{ナニ} }{12}\pi, \beta=\dfrac{\myBox{ヌネ} }{12}\pi \]のとき、 $s=t=0$ である。
解説
この場合、図は次のようになっています。
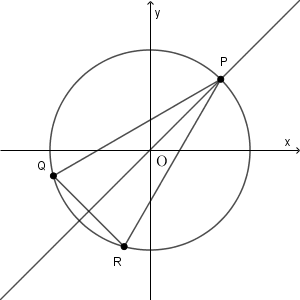
このとき
\begin{eqnarray}
s
&=&
\cos\theta + \cos\alpha + \cos\beta \\[5pt]
&=&
\cos\frac{\pi}{4} + \cos\alpha + \sin\alpha \\[5pt]
&=&
\frac{\sqrt{2} }{2} + \sin\alpha + \cos\alpha \\[5pt]
\end{eqnarray}であり、
\begin{eqnarray}
t
&=&
\sin\theta + \sin\alpha + \sin\beta \\[5pt]
&=&
\sin\frac{\pi}{4} + \sin\alpha + \cos\alpha \\[5pt]
&=&
\frac{\sqrt{2} }{2} + \sin\alpha + \cos\alpha \\[5pt]
\end{eqnarray}となることがわかります。
三角関数の合成から
\begin{eqnarray}
\sin\alpha+\cos\alpha
&=&
\sqrt{2}\left(\frac{\sqrt{2} }{2}\sin\alpha+\frac{\sqrt{2} }{2}\cos\alpha\right) \\[5pt]
&=&
\sqrt{2}\left(\sin\alpha\cos\frac{\pi}{4}+\cos\alpha\sin\frac{\pi}{4}\right) \\[5pt]
&=&
\sqrt{2}\sin\left(\alpha+\frac{\pi}{4}\right) \\[5pt]
\end{eqnarray}と変形できます。
最後に、これを使って $s=t=0$ になる場合を求めましょう。
\begin{eqnarray}
\frac{\sqrt{2} }{2} + \sin\alpha + \cos\alpha &=& 0 \\[5pt]
\frac{\sqrt{2} }{2} + \sqrt{2}\sin\left(\alpha+\frac{\pi}{4}\right) &=& 0 \\[5pt]
\sin\left(\alpha+\frac{\pi}{4}\right) &=& -\frac{1}{2} \\[5pt]
\end{eqnarray}であり、 $\dfrac{\pi}{4}\lt\alpha\lt\dfrac{5}{4}\pi$ なので、これが成り立つのは $\alpha+\dfrac{\pi}{4}=\dfrac{7}{6}\pi$ のときだけです。よって、\[ \alpha=\frac{7}{6}\pi-\dfrac{\pi}{4}=\dfrac{11}{12}\pi \]となります。
このときの $\beta$ は、 $\dfrac{\alpha+\beta}{2}=\dfrac{5}{4}\pi$ なので\[ \beta=\frac{5}{2}\pi-\frac{11}{12}\pi=\frac{19}{12}\pi \]と求められます。
解答
チツ:22
テト:24
ナニヌネ:1119
解答編 つづき
(2) 次に、 $s$ と $t$ の値を定めたときの $\theta$, $\alpha$, $\beta$ の関係について考察しよう。
考察3
$s=t=0$ の場合を考える。この場合、 $\sin^2\theta+\cos^2\theta=1$ により、 $\alpha$ と $\beta$ について考えると\[ \cos\alpha\cos\beta+\sin\alpha\sin\beta=\dfrac{\myBox{ノハ} }{\myBox{ヒ} } \]である。
同様に、 $\theta$ と $\alpha$ について考えると\[ \cos\theta\cos\alpha+\sin\theta\sin\alpha=\dfrac{\mybox{ノハ} }{\mybox{ヒ} } \]であるから、 $\theta$, $\alpha$, $\beta$ の範囲に注意すると\[ \beta-\alpha=\alpha-\theta=\dfrac{\myBox{フ} }{\myBox{ヘ} }\pi \]という関係が得られる。
解説
$s=t=0$ のとき、 $\cos\theta=-\cos\alpha-\cos\beta$, $\sin\theta=-\sin\alpha-\sin\beta$ が成り立つので
\begin{eqnarray}
\sin^2\theta+\cos^2\theta &=& 1 \\[5pt]
(-\sin\alpha-\sin\beta)^2+(-\cos\alpha-\cos\beta)^2 &=& 1 \\[5pt]
\end{eqnarray}が成り立ちます。 $\sin^2\alpha+\cos^2\alpha=1$, $\sin^2\beta+\cos^2\beta=1$ であることも使えば、この式を展開して計算すると
\begin{eqnarray}
2+2\sin\alpha\sin\beta+2\cos\alpha\cos\beta &=& 1 \\[5pt]
\cos\alpha\cos\beta+\sin\alpha\sin\beta &=& -\dfrac{1}{2} \\[5pt]
\end{eqnarray}となります。
同様に計算すれば\[ \cos\theta\cos\alpha+\sin\theta\sin\alpha=-\dfrac{1}{2} \]となることもわかります。
ここで
\begin{eqnarray}
\cos\alpha\cos\beta+\sin\alpha\sin\beta &=& -\dfrac{1}{2} \\[5pt]
\cos(\alpha-\beta) &=& -\dfrac{1}{2} \\[5pt]
\cos(\beta-\alpha) &=& -\dfrac{1}{2}
\end{eqnarray}が成り立ち、同様に $\cos(\alpha-\theta) = -\dfrac{1}{2}$ も成り立ちます。
$\beta-\alpha\gt 0$, $\alpha-\theta\gt 0$ なので、 $\beta-\alpha$ や $\alpha-\theta$ の値は、 $\dfrac{2}{3}\pi$ や $\dfrac{4}{3}\pi$ などの候補がありますが、 $\theta\gt 0$ で $\beta\lt 2\pi$ であることから、\[ \beta-\alpha=\alpha-\theta=\dfrac{2}{3}\pi \]しかありえないことがわかります。
解答
ノハヒ:-12
フヘ:23
解答編 つづき
(3) これまでの考察を振り返ると、次の 0 ~ 3 のうち、正しいものは $\dBox{ホ}$ であることがわかる。
$\dbox{ホ}$ の解答群
0: $\triangle \mathrm{ PQR }$ が正三角形ならば $s=t=0$ であり、 $s=t=0$ ならば $\triangle \mathrm{ PQR }$ は正三角形である。
1: $\triangle \mathrm{ PQR }$ が正三角形ならば $s=t=0$ であるが、 $s=t=0$ であっても $\triangle \mathrm{ PQR }$ が正三角形でない場合がある。
2: $\triangle \mathrm{ PQR }$ が正三角形であっても $s=t=0$ でない場合があるが、 $s=t=0$ ならば $\triangle \mathrm{ PQR }$ は正三角形である。
3: $\triangle \mathrm{ PQR }$ が正三角形であっても $s=t=0$ でない場合があり、 $s=t=0$ であっても $\triangle \mathrm{ PQR }$ が正三角形でない場合がある。
解説
(1)の前半で見た通り、三角形 PQR が正三角形なら $s=t=0$ が成り立ちます。
一方、(2)で見た通り、 $s=t=0$ なら $\beta-\alpha=\alpha-\theta=\dfrac{2}{3}\pi$ となるしかありません。このとき、三角形 OPQ, 三角形 OQR, 三角形 ORP は互いに合同なので、三角形 PQR は正三角形になります。
よって、選択肢 0 が正しいことがわかります。
なお、(1)の後半をどうとらえればいいか少しわかりにくいかもしれません。(1)の後半部分は、 $\triangle \mathrm{ PQR }$ が二等辺三角形となる場合として、$\theta=\dfrac{\pi}{4}$ で、直線 $y=x$ について対称な場合を考えると、 $s=t=0$ なら $\alpha=\dfrac{11}{12}\pi$, $\beta=\dfrac{19}{12}\pi$ になる、ということでした。このとき $\beta-\alpha=\alpha-\theta=\dfrac{2}{3}\pi$ が成り立つので、結局、正三角形になってしまう、という例になっています。つまり、二等辺三角形のケースで「 $s=t=0$ だが正三角形ではない例」が作れるか考えてみたけど作れなかった、ということです。分数のせいで、少し正三角形だと気づきにくいかもしれません。
解答
ホ:0





