共通テスト 数学II・数学B 2017年度プレテスト 第2問 解説
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
$a$ を定数とする。関数 $f(x)$ に対し、 $\displaystyle S(x)=\int_a^x f(t)dt$ とおく。このとき、関数 $S(x)$ の増減から $y=f(x)$ のグラフの概形を考えよう。
(1) $S(x)$ は3次関数であるとし、 $y=S(x)$ のグラフは次の図のように、2点 $(-1,0)$, $(0,4)$ を通り、点 $(2,0)$ で $x$ 軸に接しているとする。
このとき、\[ S(x)=\left(x+\myBox{ア}\right)\left(x+\myBox{イ}\right)^{\myBox{ウ} } \]である。 $S(a)=\myBox{エ}$ であるから、 $a$ を負の定数とするとき、 $a=\myBox{オカ}$ である。
関数 $S(x)$ は $x=\myBox{キ}$ を境に増加から減少に移り、 $x=\myBox{ク}$ を境に減少から増加に移っている。したがって、関数 $f(x)$ について、 $x=\mybox{キ}$ のとき $\myBox{ケ}$ であり、 $x=\mybox{ク}$ のとき $\myBox{コ}$ である。また、 $\mybox{キ}\lt x\lt \mybox{ク}$ の範囲では $\myBox{サ}$ である。
$\myBox{ケ}$, $\myBox{コ}$, $\myBox{サ}$ については、当てはまるものを、次の 0 ~ 4 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $f(x)$ の値は $0$
1: $f(x)$ の値は正
2: $f(x)$ の値は負
3: $f(x)$ は極大
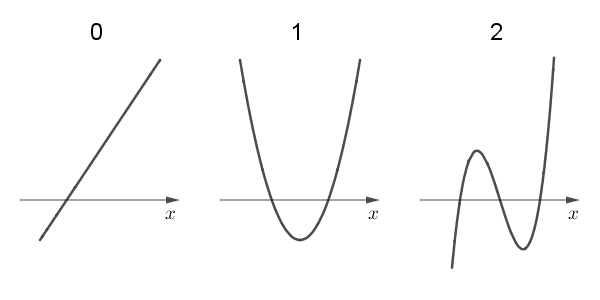
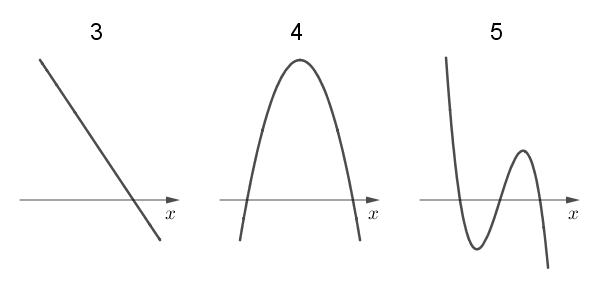
4: $f(x)$ は極小$y=f(x)$ のグラフの概形として最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。 $\myBox{シ}$
(2) (1)からわかるように、関数 $S(x)$ の増減から $y=f(x)$ のグラフの概形を考えることができる。
$a=0$ とする。次の 0 ~ 4 は $y=S(x)$ のグラフの概形と $y=f(x)$ のグラフの概形の組である。このうち、 $\displaystyle S(x)=\int_a^x f(t)dt$ の関係と矛盾するものを二つ選べ。 $\myBox{ス}$
考え方
計算はほとんどないので、その点では楽です。ただ、定積分と微分との関係を理解していないと、どのように考えていけばわからない問題が並んでいます。
$S(x)$ を微分するとどうなるか、がわからなかったとしても、 $f(x)$ の値が正や負の区間で $S(x)$ がどのように変化するか、を考えることで解くこともできます。
【必答問題】
解答編
問題
$a$ を定数とする。関数 $f(x)$ に対し、 $\displaystyle S(x)=\int_a^x f(t)dt$ とおく。このとき、関数 $S(x)$ の増減から $y=f(x)$ のグラフの概形を考えよう。
(1) $S(x)$ は3次関数であるとし、 $y=S(x)$ のグラフは次の図のように、2点 $(-1,0)$, $(0,4)$ を通り、点 $(2,0)$ で $x$ 軸に接しているとする。
このとき、\[ S(x)=\left(x+\myBox{ア}\right)\left(x+\myBox{イ}\right)^{\myBox{ウ} } \]である。
解説
$S(x)=0$ は三次方程式で、解が $x=-1,2$ であり、 $x=2$ が重解であることから、 $S(x)=m(x+1)(x-2)^2$ と書けることがわかります。さらに、 $S(0)=4$ なので、 $4m=4$ から $m=1$ とわかります。よって、\[ S(x)=(x+1)(x-2)^2 \]となります。
解答
アイウ:122
解答編 つづき
問題
$S(a)=\myBox{エ}$ であるから、 $a$ を負の定数とするとき、 $a=\myBox{オカ}$ である。
解説
$a$ から $a$ までの積分は $0$ なので、\[ S(a)=\int_a^a f(t)dt=0 \]となります。 $S(a)=0$ を満たすものは $a=-1,2$ なので、負の値なら $-1$ となります。
解答
エ:0
オカ:-1
参考
解答編 つづき
問題
関数 $S(x)$ は $x=\myBox{キ}$ を境に増加から減少に移り、 $x=\myBox{ク}$ を境に減少から増加に移っている。したがって、関数 $f(x)$ について、 $x=\mybox{キ}$ のとき $\myBox{ケ}$ であり、 $x=\mybox{ク}$ のとき $\myBox{コ}$ である。また、 $\mybox{キ}\lt x\lt \mybox{ク}$ の範囲では $\myBox{サ}$ である。
$\myBox{ケ}$, $\myBox{コ}$, $\myBox{サ}$ については、当てはまるものを、次の 0 ~ 4 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $f(x)$ の値は $0$
1: $f(x)$ の値は正
2: $f(x)$ の値は負
3: $f(x)$ は極大
4: $f(x)$ は極小
解説
$y=S(x)$ のグラフを見ながら考えましょう。
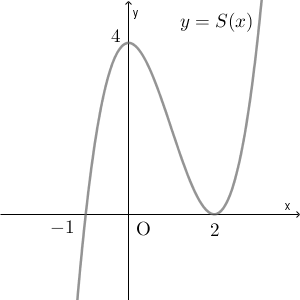
グラフを見ると、 $y=S(x)$ の値は $x=0$ までは右肩上がりで、ここを境に減少へと変わっています。なので、 $S'(x)$ は $x=0$ の前後で、正から負へと変わります。 $\displaystyle S(x)=\int_a^x f(t)dt$ だから $S'(x)=f(x)$ となるので、 $x=0$ では $f(x)$ の値は $0$ になります。
その後、 $y=S(x)$ の値は $x=2$ までは減少し続け、ここを境に増加へと変わっています。なので、 $S'(x)$ は $x=2$ の前後で、負から正へとかわります。 $S'(x)=f(x)$ なので、 $x=2$ でも $f(x)$ の値は $0$ になります。
$0\lt x\lt 2$ の範囲では、 $\displaystyle S(x)=\int_a^x f(t)dt$ の値は減り続けるので、この範囲では $S'(x)=f(x)$ の値は負であることがわかります。
選択肢に「極大」「極小」がありますが、「 $x=0$ で $S(x)$ は極大」「 $x=2$ で $S(x)$ は極小」と言えますが、 $f(x)$ は $x=0,2$ のときに極大・極小となるわけではありません。
解答
キク:02
ケコサ:002
参考
解答編 つづき
問題
$y=f(x)$ のグラフの概形として最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。 $\myBox{シ}$
解説
先ほど見たように、 $f(x)$ の値は $x\lt 0$ で正、 $0\lt x \lt 2$ で負、 $x\gt 2$ で正であり、 $x=0,2$ で $f(x)=0$ となります。これに該当する選択肢は 1 だけです。
解答
シ:1
解答編 つづき
問題
(2) (1)からわかるように、関数 $S(x)$ の増減から $y=f(x)$ のグラフの概形を考えることができる。
$a=0$ とする。次の 0 ~ 4 は $y=S(x)$ のグラフの概形と $y=f(x)$ のグラフの概形の組である。このうち、 $\displaystyle S(x)=\int_a^x f(t)dt$ の関係と矛盾するものを二つ選べ。 $\myBox{ス}$
解説
$x$ が増えていったときに、 $S(x),f(x)$ の値がどう変化するか、どういう値をとるか、に注目します。
$\displaystyle S(x)=\int_a^x f(t)dt$ から、 $S'(x)=f(x)$ が成り立ちます。 $S(x)$ が増え続けるならその範囲では $f(x)$ は正、減り続けるなら $f(x)$ は負です。これをもとに考えていきます。
0 は、 $S(x)$ は最初減り続け、 $0$ と $1$ の間で増加に切り替わっています。そのため、 $f(x)$ は最初負の値で、 $0$ と $1$ の間で負から正の値に切り替わっていないとダメです。グラフを見るとそうなっているので、矛盾はしません。
1 は、 $S(x)$ は最初増え続け、 $0$ と $1$ の間で減少に切り替わっています。そのため、 $f(x)$ は最初正の値で、 $0$ と $1$ の間で正から負の値に切り替わっていないとダメです。グラフを見ると、 $f(x)$ が正の値から負の値に切り替わっているのは $x$ が負のときなので、矛盾していることがわかります。
2 は、 $S(x)$ は一定のペースで増え続けています。なので、 $f(x)$ は、一定の正の値をとらないとダメですが、グラフを見るとそうなっているので、矛盾しません。
3 は、 $S(x)$ は最初増え続け、 $0$ と $1$ の間で少し止まって、また増加し続けています。そのため、 $f(x)$ は最初正の値で、 $0$ と $1$ の間で $0$ に近い値をとった後、再び正の値をとっていないとダメです。グラフを見るとそうなっているので、矛盾しません。
4 は、 $S(x)$ は、「減少、増加、減少、増加」となっているので、 $f(x)$ は「負、正、負、正」という順番で値をとらないとダメです。しかし、 $y=f(x)$ のグラフを見ると「正、負、正、負」という順番で値をとっているので、矛盾します。
以上から、1 と 4 が矛盾することがわかります。
解答
ス:1, 4