共通テスト 数学I・数学A 2021年度追試 第5問 解説

【第3問～第5問から2問選択】

問題編

問題

　点 Z を端点とする半直線 ZX と半直線 ZY があり、 $0^{\circ}\lt \angle \mathrm{ XZY }\lt 90^{\circ}$ とする。また、 $0^{\circ}\lt\angle \mathrm{ SZX }\lt\angle \mathrm{ XZY }$ かつ $0^{\circ}\lt\angle \mathrm{ SZY }\lt\angle \mathrm{ XZY }$ を満たす点 S をとる。点 S を通り、半直線 ZX と半直線 ZY の両方に接する円を作図したい。

　円 O を、次の(Step 1)～(Step 5)の手順で作図する。

手順
(Step 1)　$\angle \mathrm{ XZY }$ の二等分線 $\ell$ 上に点 C をとり、下図のように半直線 ZX と半直線 ZY の両方に接する円 C を作図する。また、円 C と半直線 ZX との接点を D 、半直線 ZY との接点を E とする。
(Step 2)　円 C と直線 ZS との交点の一つを G とする。
(Step 3)　半直線 ZX 上に点 H を $\mathrm{ DG }/\!/\mathrm{ HS }$ を満たすようにとる。
(Step 4)　点 H を通り、半直線 ZX に垂直な直線を引き、 $\ell$ との交点を O とする。
(Step 5)　点 O を中心とする半径 OH の円 O をかく。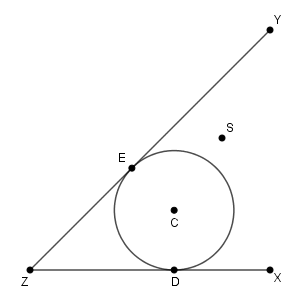

(1) (Step 1)～(Step 5)の手順で作図した円 O が求める円であることは、次の構想に基づいて下のように説明できる。

構想
円 O が点 S を通り、半直線 ZX と半直線 ZY の両方に接する円であることを示すには、 $\mathrm{ OH }=\dBox{ア}$ が成り立つことを示せばよい。

　作図の手順より、 $\triangle \mathrm{ ZDG }$ と $\triangle \mathrm{ ZHS }$ との関係、および $\triangle \mathrm{ ZDC }$ と $\triangle \mathrm{ ZHO }$ との関係に着目すると
\begin{eqnarray} \mathrm{ DG }\ :\ \dBox{イ} &=& \dBox{ウ} \ : \ \dBox{エ} \\[5pt] \mathrm{ DC }\ :\ \dBox{オ} &=& \dbox{ウ} \ : \ \dbox{エ} \\[5pt] \end{eqnarray}であるから、 $\mathrm{ DG }\ :\ \dbox{イ}\ = \ \mathrm{ DC }\ : \ \dbox{オ}$ となる。

　ここで、3点 S, O, H が一直線上にない場合は、 $\angle \mathrm{ CDG }=\angle \ \dBox{カ}$ であるので、 $\triangle \mathrm{ CDG }$ と $\triangle \ \dbox{カ}$ との関係に着目すると、 $\mathrm{ CD=CG }$ より $\mathrm{ OH }=\dbox{ア}$ であることがわかる。

　なお、3点 S, O, H が一直線上にある場合は、 $\mathrm{ DG }=\myBox{キ} \mathrm{ DC }$ となり、 $\mathrm{ DG }\ : \ \dbox{イ}\ = \ \mathrm{ DC }\ :\ \dbox{オ}$ より $\mathrm{ OH }=\dbox{ア}$ であることがわかる。

$\dbox{ア}$ ～ $\dbox{オ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\mathrm{ DH }$
　1: $\mathrm{ HO }$
　2: $\mathrm{ HS }$
　3: $\mathrm{ OD }$
　4: $\mathrm{ OG }$
　5: $\mathrm{ OS }$
　6: $\mathrm{ ZD }$
　7: $\mathrm{ ZH }$
　8: $\mathrm{ ZO }$
　9: $\mathrm{ ZS }$

$\dbox{カ}$ の解答群

　0: $\mathrm{ OHD }$
　1: $\mathrm{ OHG }$
　2: $\mathrm{ OHS }$
　3: $\mathrm{ ZDS }$
　4: $\mathrm{ ZHG }$
　5: $\mathrm{ ZHS }$
　6: $\mathrm{ ZOS }$
　7: $\mathrm{ ZCG }$

(2) 点 S を通り、半直線 ZX と半直線 ZY の両方に接する円は二つ作図できる。特に、点 S が $\angle \mathrm{ XZY }$ の二等分線 $\ell$ 上にある場合を考える。半径が大きい方の円の中心を $\mathrm{ O }_1$ とし、半径が小さい方の円の中心を $\mathrm{ O }_2$ とする。また、円 $\mathrm{ O }_2$ と半直線 ZY が接する点を I とする。円 $\mathrm{ O }_1$ と半直線 ZY が接する点を J とし、円 $\mathrm{ O }_1$ と半直線 ZX が接する点を K とする。

　作図をした結果、円 $\mathrm{ O }_1$ の半径は $5$ 、円 $\mathrm{ O }_2$ の半径は $3$ であったとする。このとき、 $\mathrm{ IJ }=\myBox{ク}\sqrt{\myBox{ケコ} }$ である。さらに、円 $\mathrm{ O }_1$ と円 $\mathrm{ O }_2$ の接点 S における共通接線と半直線 ZY との交点を L とし、直線 LK と円 $\mathrm{ O }_1$ との交点で点 K とは異なる点を M とすると\[ \mathrm{ LM\cdot LK }=\myBox{サシ} \]である。

　また、 $\mathrm{ ZI }=\myBox{ス}\sqrt{\myBox{セソ} }$ であるので、直線 LK と直線 $\ell$ との交点を N とすると\[ \dfrac{\mathrm{ LN } }{\mathrm{ NK } } =\dfrac{\myBox{タ} }{\myBox{チ} }\ ,\ \mathrm{ SN } =\dfrac{\myBox{ツ} }{\myBox{テ} } \]である。

考え方

前半は作図を扱っていて珍しい内容です。ただ、聞かれていることは、なぜこの作図の方法が正しいかであり、証明の穴埋めのような問題になっています。相似などの図形の性質を用いて答えていきます。「 S, O, H が一直線上にある場合」は、そもそもどういう場合なのかがわかりづらいですが、これが成り立つときに図がどのようになっていないといけないかを考えると、少し状況がわかりやすくなるかもしれません。

(2)は設定は共通していますが、使う道具はかなり変わります。頭を切り替えて考えていきましょう。接線、円、角の二等分線など使える条件がたくさんあるため、適切な条件を選ぶのが大変です。よく練習しておかないと難しいです。

解答編

問題

　点 Z を端点とする半直線 ZX と半直線 ZY があり、 $0^{\circ}\lt \angle \mathrm{ XZY }\lt 90^{\circ}$ とする。また、 $0^{\circ}\lt\angle \mathrm{ SZX }\lt\angle \mathrm{ XZY }$ かつ $0^{\circ}\lt\angle \mathrm{ SZY }\lt\angle \mathrm{ XZY }$ を満たす点 S をとる。点 S を通り、半直線 ZX と半直線 ZY の両方に接する円を作図したい。

　円 O を、次の(Step 1)～(Step 5)の手順で作図する。

手順
(Step 1)　$\angle \mathrm{ XZY }$ の二等分線 $\ell$ 上に点 C をとり、下図のように半直線 ZX と半直線 ZY の両方に接する円 C を作図する。また、円 C と半直線 ZX との接点を D 、半直線 ZY との接点を E とする。
(Step 2)　円 C と直線 ZS との交点の一つを G とする。
(Step 3)　半直線 ZX 上に点 H を $\mathrm{ DG }/\!/\mathrm{ HS }$ を満たすようにとる。
(Step 4)　点 H を通り、半直線 ZX に垂直な直線を引き、 $\ell$ との交点を O とする。
(Step 5)　点 O を中心とする半径 OH の円 O をかく。

解説

参考図は、円 C を作図するところまでで終わっています。手順通りに進めていくと、図は次のようになります。

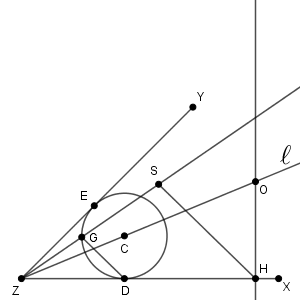
これを踏まえて、以降の問題を考えていきます。

解答編 つづき

(1) (Step 1)～(Step 5)の手順で作図した円 O が求める円であることは、次の構想に基づいて下のように説明できる。

構想
円 O が点 S を通り、半直線 ZX と半直線 ZY の両方に接する円であることを示すには、 $\mathrm{ OH }=\dBox{ア}$ が成り立つことを示せばよい。

　作図の手順より、 $\triangle \mathrm{ ZDG }$ と $\triangle \mathrm{ ZHS }$ との関係、および $\triangle \mathrm{ ZDC }$ と $\triangle \mathrm{ ZHO }$ との関係に着目すると
\begin{eqnarray} \mathrm{ DG }\ :\ \dBox{イ} &=& \dBox{ウ} \ : \ \dBox{エ} \\[5pt] \mathrm{ DC }\ :\ \dBox{オ} &=& \dbox{ウ} \ : \ \dbox{エ} \\[5pt] \end{eqnarray}であるから、 $\mathrm{ DG }\ :\ \dbox{イ}\ = \ \mathrm{ DC }\ : \ \dbox{オ}$ となる。

　ここで、3点 S, O, H が一直線上にない場合は、 $\angle \mathrm{ CDG }=\angle \ \dBox{カ}$ であるので、 $\triangle \mathrm{ CDG }$ と $\triangle \ \dbox{カ}$ との関係に着目すると、 $\mathrm{ CD=CG }$ より $\mathrm{ OH }=\dbox{ア}$ であることがわかる。

　なお、3点 S, O, H が一直線上にある場合は、 $\mathrm{ DG }=\myBox{キ} \mathrm{ DC }$ となり、 $\mathrm{ DG }\ : \ \dbox{イ}\ = \ \mathrm{ DC }\ :\ \dbox{オ}$ より $\mathrm{ OH }=\dbox{ア}$ であることがわかる。

$\dbox{ア}$ ～ $\dbox{オ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\mathrm{ DH }$
　1: $\mathrm{ HO }$
　2: $\mathrm{ HS }$
　3: $\mathrm{ OD }$
　4: $\mathrm{ OG }$
　5: $\mathrm{ OS }$
　6: $\mathrm{ ZD }$
　7: $\mathrm{ ZH }$
　8: $\mathrm{ ZO }$
　9: $\mathrm{ ZS }$

$\dbox{カ}$ の解答群

　0: $\mathrm{ OHD }$
　1: $\mathrm{ OHG }$
　2: $\mathrm{ OHS }$
　3: $\mathrm{ ZDS }$
　4: $\mathrm{ ZHG }$
　5: $\mathrm{ ZHS }$
　6: $\mathrm{ ZOS }$
　7: $\mathrm{ ZCG }$

解説

点 O を中心とし、半径 OH の円をかくことを考えます。点 O は、 $\angle \mathrm{ XZY }$ の二等分線上にあるので、半直線 ZX, ZY に接することは明らかです。なので、円 O が求める円であることを示すにはこれが S を通ること、つまり、 $\mathrm{ OH=OS }$ であることを示せばいいです。

H は、線分 DG と線分 HS が平行になるようにとったので、三角形 ZDG と三角形 ZHS は相似です。なので、\[ \mathrm{ DG:HS=ZD:ZH } \]が成り立ちます。

一方、線分 CD と線分 OH は、ともに半直線 ZX に対して垂直なので、この2つの線分は平行です。よって、三角形 ZDC と三角形 ZHO は相似です。なので、\[ \mathrm{ DC:HO=ZD:ZH } \]が成り立ちます。よって、 $\mathrm{ DG:HS=DC:HO }$ が成り立つことがわかります。

また、3点 S, O, H が一直線上にない場合は、線分 DG と線分 HS が平行であることと、線分 CD と線分 OH が平行であることから、\[ \angle \mathrm{ CDG }=\angle \mathrm{ OHS } \]となります。これと、先ほど示した $\mathrm{ DG:HS=DC:HO }$ から、三角形 CDG と三角形 OHS は相似になることがわかります。 $\mathrm{ CD=CG }$ だから、 $\mathrm{ OH=OS }$ となることがわかります。こうして、 S, O, H が一直線上にない場合に、構想にある内容が示せました。

次に、3点 S, O, H が一直線上にある場合を考えます。この場合は、先ほどのような三角形 OHS を考えることはできません。そのため、場合分けをして考えないといけないのですが、そもそもこれがどういうときなのかは少しわかりづらいです。どういう状況なのか先に考える必要があります。

S, O, H が一直線上にあるとは、 SH が半直線 ZX と垂直であるときです。 SH と DG は平行なので、 DG も半直線 ZX　と垂直になるとき、ということです。つまり、次のような状況を考える、ということです。

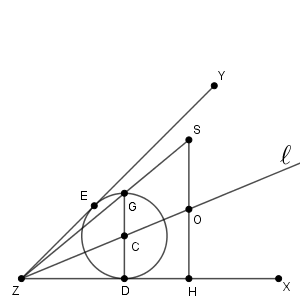
このとき、 DG は円 C の直径なので、 $\mathrm{ DG }=2\mathrm{ DC }$ となります。イ～オのところで求めた通り、 $\mathrm{ DG:HS=DC:HO }$ が成り立つので、 $\mathrm{ OH=OS }$ が成り立つことがわかります。こうして、この場合も構想にある内容が示せました。

以上より、(Step 1)～(Step 5)の手順で、求める円が作図できることがわかりました。

解答

ア：5
イウエ：267
オ：1
カ：2
キ：2

解答編 つづき

(2) 点 S を通り、半直線 ZX と半直線 ZY の両方に接する円は二つ作図できる。特に、点 S が $\angle \mathrm{ XZY }$ の二等分線 $\ell$ 上にある場合を考える。半径が大きい方の円の中心を $\mathrm{ O }_1$ とし、半径が小さい方の円の中心を $\mathrm{ O }_2$ とする。また、円 $\mathrm{ O }_2$ と半直線 ZY が接する点を I とする。円 $\mathrm{ O }_1$ と半直線 ZY が接する点を J とし、円 $\mathrm{ O }_1$ と半直線 ZX が接する点を K とする。

解説

図は次のようになっています。

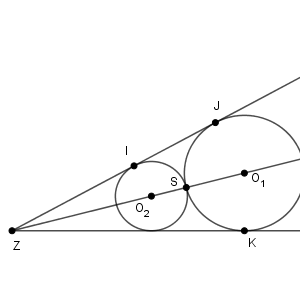
これを踏まえて考えていきます。

解答編 つづき

　作図をした結果、円 $\mathrm{ O }_1$ の半径は $5$ 、円 $\mathrm{ O }_2$ の半径は $3$ であったとする。このとき、 $\mathrm{ IJ }=\myBox{ク}\sqrt{\myBox{ケコ} }$ である。

解説

問題文にある通りに考えるよりも、次のようにしたほうが考えやすいでしょう。

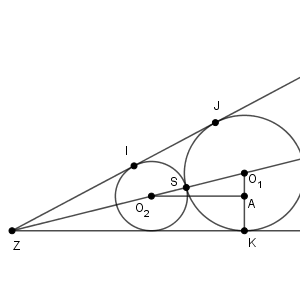
$\mathrm{ KO }_1$ を結び、この線分に $\mathrm{ O }_2$ から垂線をおろし、交点を $\mathrm{ A }$ とします。こうすると、 $\mathrm{ IJ }$ は $\mathrm{ AO }_2$ と同じ長さです。

また、三角形 $\mathrm{ O_1O_2A }$ は直角三角形であり、 $\mathrm{ O_1O_2 }=3+5=8$ で、 $\mathrm{ AO }_1=5-3=2$ なので、\[ \mathrm{ AO_2 }=\sqrt{8^2-2^2}=2\sqrt{15} \]となります。よって、 $\mathrm{ IJ }=2\sqrt{15}$ です。

解答

クケコ：215

解答編 つづき

さらに、円 $\mathrm{ O }_1$ と円 $\mathrm{ O }_2$ の接点 S における共通接線と半直線 ZY との交点を L とし、直線 LK と円 $\mathrm{ O }_1$ との交点で点 K とは異なる点を M とすると\[ \mathrm{ LM\cdot LK }=\myBox{サシ} \]である。

解説

図は次のようになっています。

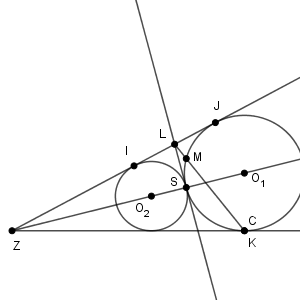
方べきの定理より、\[ \mathrm{ LM }\cdot \mathrm{ LK }=\mathrm{ LS }^2 \]となります。また、点 L から円 $\mathrm{ O }_1$, 円 $\mathrm{ O }_2$ へ接線を引いたと考えると、 $\mathrm{ LI }=\mathrm{ LS }=\mathrm{ LJ }$ であることから、 $\mathrm{ LS }$ は $\mathrm{ IJ }$ の半分だとわかります。よって、\[ \mathrm{ LM }\cdot \mathrm{ LK }=\mathrm{ LS }^2=\sqrt{15}\cdot\sqrt{15}=15 \]となります。

解答

サシ：15

解答編 つづき

　また、 $\mathrm{ ZI }=\myBox{ス}\sqrt{\myBox{セソ} }$ であるので、直線 LK と直線 $\ell$ との交点を N とすると\[ \dfrac{\mathrm{ LN } }{\mathrm{ NK } } =\dfrac{\myBox{タ} }{\myBox{チ} }\ ,\ \mathrm{ SN } =\dfrac{\myBox{ツ} }{\myBox{テ} } \]である。

解説

IJ を求めたときの図を使います。

ここで、三角形 $\mathrm{ O_1O_2A }$ と三角形 $\mathrm{ O_2ZI }$ は相似なので、 $\mathrm{ IO }_2:\mathrm{ IZ }$ は $\mathrm{ AO }_1:\mathrm{ AO }_2$ と等しく、 $2:2\sqrt{15}$ です。 $\mathrm{ IO }_2=3$ なので、\[ \mathrm{ ZI }=3\sqrt{15} \]となります。

N は次のような点です。

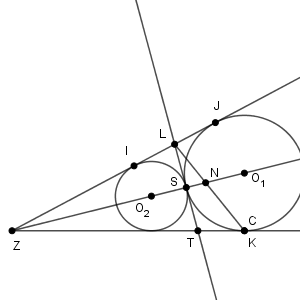
ZN は $\angle \mathrm{ LZK }$ の二等分線なので、 $\mathrm{ LN:NK=ZL:ZK }$ が成り立ちます。\[ \mathrm{ ZL }=\mathrm{ ZI }+\mathrm{ IL }=3\sqrt{15}+\sqrt{15}=4\sqrt{15} \]であり、\[ \mathrm{ ZK }=\mathrm{ ZJ }=3\sqrt{15}+2\sqrt{15}=5\sqrt{15} \]なので\[ \frac{\mathrm{ LN } }{\mathrm{ NK } } = \frac{\mathrm{ ZL } }{\mathrm{ ZK } }=\frac{4\sqrt{15} }{5\sqrt{15} }=\frac{4}{5} \]となります。

次に、 SN について考えます。三角形 $\mathrm{ ZIO_2 }$ は、 $1:\sqrt{15}:4$ の直角三角形なので、 $\mathrm{ ZO }_2=3\cdot4=12$ であり、 $\mathrm{ SZ }=12+3=15$ です。ここで、 LS と ZK との交点を T とすると、三角形 NKZ と直線 LT に対してメネラウスの定理を使えば
\begin{eqnarray} \frac{\mathrm{ NS } }{\mathrm{ SZ } }\cdot\frac{\mathrm{ ZT } }{\mathrm{ TK } }\cdot\frac{\mathrm{ KL } }{\mathrm{ LN } } &=& 1 \\[5pt] \frac{\mathrm{ NS } }{15}\cdot\frac{\mathrm{ ZL } }{\mathrm{ LJ } }\cdot\frac{\mathrm{ LN }+\mathrm{ NK } }{\mathrm{ LN } } &=& 1 \\[5pt] \frac{\mathrm{ NS } }{15}\cdot\frac{4\sqrt{15} }{\sqrt{15} }\cdot\frac{9}{4} &=& 1 \\[5pt] \mathrm{ NS } &=& \frac{15}{9}=\dfrac{5}{3} \\[5pt] \end{eqnarray}と求められます。

解答

スセソ：315
タチ：45
ツテ：53