共通テスト数学I・数学A 2021年度追試第2問 [2] 解説

🕒 2021/02/19 🔄 2023/05/01

【必答問題】

問題編

問題

（問題文の訂正内容は反映済みです）

　総務省が実施している国勢調査では都道府県ごとの総人口が調べられており、その内訳として日本人人口と外国人人口が公表されている。また、外務省では旅券（パスポート）を取得した人数を都道府県ごとに公表している。加えて、文部科学省では都道府県ごとの小学校に在籍する児童数を公表している。

　そこで、47都道府県の、人口1万人あたりの外国人人口（以下、外国人数）、人口1万人あたりの小学校児童数（以下、小学生数）、また、日本人1万人あたりの旅券を取得した人数（以下、旅券取得者数）を、それぞれ計算した。

(1) 図1は、2010年における47都道府県の、旅券取得者数（横軸）と小学生数（縦軸）の関係を黒丸で、旅券取得者数（横軸）と外国人数（縦軸）の関係を白丸で表した散布図である。

　次の(I)、(II)、(III)は図1の散布図に関する記述である。

　(I) 小学生数の四分位範囲は、外国人数の四分位範囲より大きい。
　(II) 旅券取得者数の範囲は、外国人数の範囲より大きい。
　(III) 旅券取得者数と小学生数の相関係数は、旅券取得者数と外国人数の相関係数より大きい。

(I)、(II)、(III)の正誤の組合せとして正しいものは $\dBox{ツ}$ である。

$\dbox{ツ}$ の解答群

　0: (I) 正　(II) 正　(III) 正
　1: (I) 正　(II) 正　(III) 誤
　2: (I) 正　(II) 誤　(III) 正
　3: (I) 正　(II) 誤　(III) 誤
　4: (I) 誤　(II) 正　(III) 正
　5: (I) 誤　(II) 正　(III) 誤
　6: (I) 誤　(II) 誤　(III) 正
　7: (I) 誤　(II) 誤　(III) 誤

(2) 一般に、度数分布表

階級値 $x_1$ $x_2$ $x_3$ $x_4$ $\cdots$ $x_k$ 計

度数 $f_1$ $f_2$ $f_3$ $f_4$ $\cdots$ $f_k$ $n$

が与えられていて、各階級に含まれるデータの値がすべてその階級値に等しいと仮定すると、平均値 $\bar{x}$ は\[ \bar{x}=\dfrac{1}{n}(x_1f_1+x_2f_2+x_3f_3+x_4f_4+\cdots+x_kf_k) \]で求めることができる。さらに階級の幅が一定で、その値が $h$ のときは\[ x_2=x_1+h, x_3=x_1+2h, x_4=x_1+3h, \cdots, \ x_k=x_1+(k-1)h \]に注意すると\[ \bar{x}=\dBox{テ} \]と変形できる。

$\dbox{テ}$ については、最も適当なものを、次の 0 ～ 4 のうちから一つ選べ。

　0: $\dfrac{x_1}{n}(f_1+f_2+f_3+f_4+\cdots+f_k)$

　1: $\dfrac{h}{n}(f_1+2f_2+3f_3+4f_4+\cdots+kf_k)$

　2: $x_1+\dfrac{h}{n}(f_2+f_3+f_4+\cdots+f_k)$

　3: $x_1+\dfrac{h}{n}\{f_2+2f_3+3f_4+\cdots+(k-1)f_k\}$

　4: $\dfrac{1}{2}(f_1+f_k)x_1-\dfrac{1}{2}(f_1+kf_k)$

　図2は、2008年における47都道府県の旅券取得者数のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右型の数値を含まない。

　図2のヒストグラムに関して、各階級に含まれるデータの値がすべてその階級値に等しいと仮定する。このとき平均値 $\bar{x}$ は小数第1位を四捨五入すると $\myBox{トナニ}$ である。

(3) 一般に、度数分布表

階級値 $x_1$ $x_2$ $\cdots$ $x_k$ 計

度数 $f_1$ $f_2$ $\cdots$ $f_k$ $n$

が与えられていて、各階級に含まれるデータの値がすべてその階級値に等しいと仮定すると、分散 $s^2$ は\[
s^2=\dfrac{1}{n} \left\{\left(x_1-\bar{x}\right)^2 f_1 +\left(x_2-\bar{x}\right)^2 f_2 +\cdots +\left(x_k-\bar{x}\right)^ 2f_k\right\} \]で求めることができる。さらに $s^2$ は\[ s^2=\dfrac{1}{n} \left\{ \left(x_1^2f_1+x_2^2f_2+\cdots+x_k^2f_k\right) -2\bar{x}\times\dBox{ヌ} +\left(\bar{x}\right)^2\times\dBox{ネ} \right\} \]と変形できるので\[ s^2=\dfrac{1}{n}(x_1^2f_1+x_2^2f_2+\cdots x_k^2f_k)-\dBox{ノ}\quad\cdots① \]である。

$\dbox{ヌ}$ ～ $\dbox{ノ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $n$
　1: $n^2$
　2: $\bar{x}$
　3: $n\bar{x}$
　4: $2n\bar{x}$
　5: $n^2\bar{x}$
　6: $\left(\bar{x}\right)^2$
　7: $n\left(\bar{x}\right)^2$
　8: $2n\left(\bar{x}\right)^2$
　9: $3n\left(\bar{x}\right)^2$

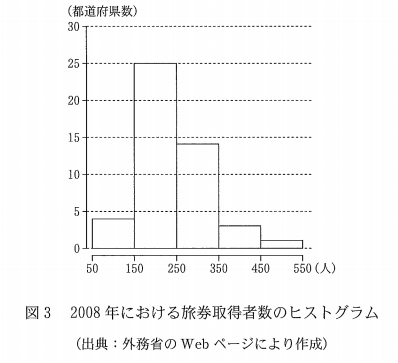
　図3は、図2を再掲したヒストグラムである。

　図3のヒストグラムに関して、各階級に含まれるデータの値がすべてその階級値に等しいと仮定すると、平均値 $\bar{x}$ は(2)で求めた $\mybox{トナニ}$ であり。 $\mybox{トナニ}$の値と式①を用いると、分散 $s^2$ は $\dBox{ハ}$ である。

$\dbox{ハ}$ については、最も近いものを、次の 0 ～ 7 のうちから一つ選べ。

　0: 3900
　1: 4900
　2: 5900
　3: 6900
　4: 7900
　5: 8900
　6: 9900
　7: 10900

考え方

(1)は、四分位範囲、範囲、相関係数が全部わかっていないと正解できません。定義がわかっていれば選ぶのは難しくないですが、分野の範囲全体をおさえていないといけません。

(2)と(3)は、抽象的な計算が苦手な人にはつらい問題です。どちらも、抽象的な計算をした後に、それを使って具体的な計算をしてみましょう、という流れなので、前半ができないと後半を解くのも難しくなります。

計算を頑張ればできるかもしれませんが、愚直に計算するのは、それはそれで厳しいです。特に(3)の後半はかなり大変になってしまいます。

なかなか点数のとりにくいセットだと思います。

解答編

問題

　総務省が実施している国勢調査では都道府県ごとの総人口が調べられており、その内訳として日本人人口と外国人人口が公表されている。また、外務省では旅券（パスポート）を取得した人数を都道府県ごとに公表している。加えて、文部科学省では都道府県ごとの小学校に在籍する児童数を公表している。

　そこで、47都道府県の、人口1万人あたりの外国人人口（以下、外国人数）、人口1万人あたりの小学校児童数（以下、小学生数）、また、日本人1万人あたりの旅券を取得した人数（以下、旅券取得者数）を、それぞれ計算した。

(1) 図1は、2010年における47都道府県の、旅券取得者数（横軸）と小学生数（縦軸）の関係を黒丸で、旅券取得者数（横軸）と外国人数（縦軸）の関係を白丸で表した散布図である。

　次の(I)、(II)、(III)は図1の散布図に関する記述である。

　(I) 小学生数の四分位範囲は、外国人数の四分位範囲より大きい。
　(II) 旅券取得者数の範囲は、外国人数の範囲より大きい。
　(III) 旅券取得者数と小学生数の相関係数は、旅券取得者数と外国人数の相関係数より大きい。

(I)、(II)、(III)の正誤の組合せとして正しいものは $\dBox{ツ}$ である。

$\dbox{ツ}$ の解答群

　0: (I) 正　(II) 正　(III) 正
　1: (I) 正　(II) 正　(III) 誤
　2: (I) 正　(II) 誤　(III) 正
　3: (I) 正　(II) 誤　(III) 誤
　4: (I) 誤　(II) 正　(III) 正
　5: (I) 誤　(II) 正　(III) 誤
　6: (I) 誤　(II) 誤　(III) 正
　7: (I) 誤　(II) 誤　(III) 誤

解説

順番に見ていきます。

小学生数は、黒丸を縦方向に見ます。外国人数は白丸を縦方向に見ます。黒丸は上の方に飛びぬけているものもありますが、だいたい500～600の間に収まっています。一方、白丸は0～200まで、バラバラに分布しています。四分位範囲とは、第3四分位数と第1四分位数との差なので、小学生数のほうが小さいです。そのため、(I)は誤りです。

旅券取得者数と外国人数の関係は、白丸を横方向と縦方向に見ればいいです。左端から右端まで400人程度ですが、縦方向には200人程度の幅しかありません。範囲とは、最大値と最小値との差なので、旅券取得者数のほうが大きいです。そのため、(II)は正しいです。

相関とは、「片方が大きいときにもう片方も大きい、片方が小さいときにもう片方も小さい」という関係のことで、この関係の強さを表したものが相関係数です。黒丸を見るとほぼ横一直線に並んでいますが、白丸は右肩上がりの直線に近い形で並んでいます。そのため、旅券取得者数と外国人数の相関係数のほうが大きいです。(III)は誤りです。

これより、選択肢の中では、5が正解だとわかります。

解答

ツ：5

解答編つづき

(2) 一般に、度数分布表

階級値 $x_1$ $x_2$ $x_3$ $x_4$ $\cdots$ $x_k$ 計

度数 $f_1$ $f_2$ $f_3$ $f_4$ $\cdots$ $f_k$ $n$

が与えられていて、各階級に含まれるデータの値がすべてその階級値に等しいと仮定すると、平均値 $\bar{x}$ は\[ \bar{x}=\dfrac{1}{n}(x_1f_1+x_2f_2+x_3f_3+x_4f_4+\cdots+x_kf_k) \]で求めることができる。さらに階級の幅が一定で、その値が $h$ のときは\[ x_2=x_1+h, x_3=x_1+2h, x_4=x_1+3h, \cdots, \ x_k=x_1+(k-1)h \]に注意すると\[ \bar{x}=\dBox{テ} \]と変形できる。

$\dbox{テ}$ については、最も適当なものを、次の 0 ～ 4 のうちから一つ選べ。

　0: $\dfrac{x_1}{n}(f_1+f_2+f_3+f_4+\cdots+f_k)$

　1: $\dfrac{h}{n}(f_1+2f_2+3f_3+4f_4+\cdots+kf_k)$

　2: $x_1+\dfrac{h}{n}(f_2+f_3+f_4+\cdots+f_k)$

　3: $x_1+\dfrac{h}{n}\{f_2+2f_3+3f_4+\cdots+(k-1)f_k\}$

　4: $\dfrac{1}{2}(f_1+f_k)x_1-\dfrac{1}{2}(f_1+kf_k)$

　図2は、2008年における47都道府県の旅券取得者数のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右型の数値を含まない。

　図2のヒストグラムに関して、各階級に含まれるデータの値がすべてその階級値に等しいと仮定する。このとき平均値 $\bar{x}$ は小数第1位を四捨五入すると $\myBox{トナニ}$ である。

解説

平均値は、すべての値を足して個数で割って求めます。問題文にある通り、 $x_i$ の値が $f_i$ 個ある場合（ $i=1,2,\cdots ,n$ ）は、 $x_if_i$ をそれぞれ計算してすべて足し合わせて $n$ で割れば、平均値 $\bar{x}$ が求められます。

また、階級の幅が $h$ で一定である場合は、 $x_1$ と $x_i$ は $(i-1)h$ だけ離れていることになります。そのため、\[ x_if_i=\{x_1+(i-1)h\}f_i = x_1f_i +(i-1)f_ih \]と変形できます。これを $i=1$ から $i=n$ まで足して $n$ で割るとどうなるかを考えます。 $f_i$ はすべて足すと $n$ になるので、1項目の部分からは $x_1$ が出てきます。このことから、 $\bar{x}$ は\[ x_1+\dfrac{h}{n}\{f_2+2f_3+3f_4+\cdots+(k-1)f_k\} \]と書けることがわかります。

これを使って与えられたヒストグラムから平均値を計算します。 $x_1=100$ で、 $h=100$ とすればいいので
\begin{eqnarray} \bar{x} &=& 100+\frac{100}{47}\{ 25+2\cdot14+3\cdot3+4\cdot1 \} \\[5pt] &=& 100+\frac{100\cdot66}{47} \\[5pt] &=& 240.4\cdots \end{eqnarray}と求められます。

なお、テの部分は、答えを選ぶだけであれば、具体的な値から絞っていくこともできます。例えば、 $h=10$ で、 $x_1=0$, $x_k=100$, $f_1=f_k=1$ で他の $f_i$ は全部 0 だとしましょう。2人がテストを受けて、1人が0点、1人が100点、という状況です。平均値はもちろん50点です。

この場合、選択肢0は明らかにおかしいです。 $x_k$ の情報が入っていないので、これで平均が計算できるわけがありません。選択肢1は、 $x_1$ の情報がないので、これもおかしいでしょう。選択肢2は、 $x_k$ の値が反映されないのでおかしいです。選択肢4は、等差数列の和を意識した式かもしれませんが、これも正しく計算できません。

うまい例を考えること自体が難しいですが、選択肢0, 1, 2などは意味を考えればすぐに捨てることはできます。

解答

テ：3
トナニ：240

解答編つづき

(3) 一般に、度数分布表

階級値 $x_1$ $x_2$ $\cdots$ $x_k$ 計

度数 $f_1$ $f_2$ $\cdots$ $f_k$ $n$

が与えられていて、各階級に含まれるデータの値がすべてその階級値に等しいと仮定すると、分散 $s^2$ は\[
s^2=\dfrac{1}{n} \left\{\left(x_1-\bar{x}\right)^2 f_1 +\left(x_2-\bar{x}\right)^2 f_2 +\cdots +\left(x_k-\bar{x}\right)^ 2f_k\right\} \]で求めることができる。さらに $s^2$ は\[ s^2=\dfrac{1}{n} \left\{ \left(x_1^2f_1+x_2^2f_2+\cdots+x_k^2f_k\right) -2\bar{x}\times\dBox{ヌ} +\left(\bar{x}\right)^2\times\dBox{ネ} \right\} \]と変形できるので\[ s^2=\dfrac{1}{n}(x_1^2f_1+x_2^2f_2+\cdots x_k^2f_k)-\dBox{ノ}\quad\cdots① \]である。

$\dbox{ヌ}$ ～ $\dbox{ノ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $n$
　1: $n^2$
　2: $\bar{x}$
　3: $n\bar{x}$
　4: $2n\bar{x}$
　5: $n^2\bar{x}$
　6: $\left(\bar{x}\right)^2$
　7: $n\left(\bar{x}\right)^2$
　8: $2n\left(\bar{x}\right)^2$
　9: $3n\left(\bar{x}\right)^2$

　図3は、図2を再掲したヒストグラムである。

　図3のヒストグラムに関して、各階級に含まれるデータの値がすべてその階級値に等しいと仮定すると、平均値 $\bar{x}$ は(2)で求めた $\mybox{トナニ}$ であり。 $\mybox{トナニ}$の値と式①を用いると、分散 $s^2$ は $\dBox{ハ}$ である。

$\dbox{ハ}$ については、最も近いものを、次の 0 ～ 7 のうちから一つ選べ。

　0: 3900
　1: 4900
　2: 5900
　3: 6900
　4: 7900
　5: 8900
　6: 9900
　7: 10900

解説

分散は、各値と平均値との差を2乗し、足し合わせて個数で割って求めます。問題文にある通り、 $x_i$ の値が $f_i$ 個ある場合は、 $\left(x_i-\bar{x}\right)^2\times f_i$ を足し合わせて $n$ で割ればいいです。

ここで、
\begin{eqnarray} & & \left(x_i-\bar{x}\right)^2\times f_i \\[5pt] &=& x_i^2f_i -2\bar{x}x_if_i +\left(\bar{x}\right)^2f_i \\[5pt] \end{eqnarray}と変形できます。この2項目を $i=1$ から $i=k$ まで足し合わせると \begin{eqnarray} -2\bar{x}(x_1f_1+x_2f_2+\cdots+x_k f_k) \end{eqnarray}となりますが、このカッコ内の部分は、平均値を計算するときにも出てきました。このカッコ内を $n$ で割れば平均値 $\bar{x}$ になるので、この値は\[ -2\bar{x}\times n\bar{x} \]と変形できます。

次に、先ほどの3項目 $\left(\bar{x}\right)^2f_i$ を考えます。これを $i=1$ から $i=k$ まで足すと、
\begin{eqnarray} \left(\bar{x}\right)^2\times(f_1+f_2+\cdots+f_k) \end{eqnarray}となりますが、2つ目のカッコ内の和は $n$ になります。

以上から、分散 $s^2$ は
\begin{eqnarray} & & s^2 \\[5pt] &=& \dfrac{1}{n} \left\{ \left(x_1^2f_1+x_2^2f_2+\cdots+x_k^2f_k\right) -2\bar{x}\times n\bar{x} +\left(\bar{x}\right)^2\times n \right\} \\[5pt] &=& \dfrac{1}{n} \left\{ \left(x_1^2f_1+x_2^2f_2+\cdots+x_k^2f_k\right) -n\left(\bar{x}\right)^2 \right\} \\[5pt] &=& \dfrac{1}{n}\left(x_1^2f_1+x_2^2f_2+\cdots+x_k^2f_k\right) -\left(\bar{x}\right)^2 \end{eqnarray}となります。

これをもとに、ヒストグラムから分散を計算します。平均値は $240$ だったので
\begin{eqnarray} & & s^2 \\[5pt] &=& \frac{1}{47} \left( 100^2\cdot 4 + 200^2\cdot 25 + 300^2\cdot 14 + 400^2\cdot 3 + 500^2\cdot 1 \right) -240^2 \\[5pt] &=& \frac{100^2}{47} \left( 4 + 4\cdot 25 + 9\cdot 14 + 16\cdot 3 + 25 \right) -240^2 \\[5pt] &=& \frac{100^2}{47} \left( 4 + 100 + 126 + 48 + 25 \right) -240^2 \\[5pt] &=& \frac{100^2}{47}\cdot 303 -240^2 \\[5pt] &=& 6868.0\cdots \end{eqnarray}となるので、選択肢3が一番近いことがわかります。