共通テスト 数学I・数学A 2021年度追試 第1問 [2] 解説
【必答問題】
問題編
問題
平面上に2点 A, B があり、 $\mathrm{AB}=8$ である。直線 AB 上にない点 P をとり、 $\triangle \mathrm{ ABP }$ をつくり、その外接円の半径を $R$ とする。
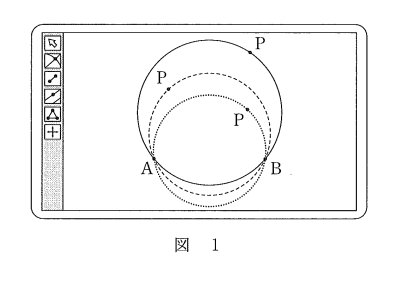
太郎さんは、図1のように、コンピュータソフトを使って点 P をいろいろな位置にとった。
図1は、点 P をいろいろな位置にとったときの $\triangle \mathrm{ ABP }$ の外接円をかいたものである。
(1) 太郎さんは、点 P のとり方によって外接円の半径が異なることに気づき、次の問題1を考えることにした。
問題1
点 P をいろいろな位置にとるとき、外接円の半径 $R$ が最小となる $\triangle \mathrm{ ABP }$ はどのような三角形か。正弦定理により、 $2R=\dfrac{\myBox{キ} }{\sin\angle \mathrm{ APB } }$ である。よって、 $R$ が最小となるのは $\angle \mathrm{ APB }=\myBox{クケ}^{\ \circ}$ の三角形である。このとき、 $R=\myBox{コ}$ である。
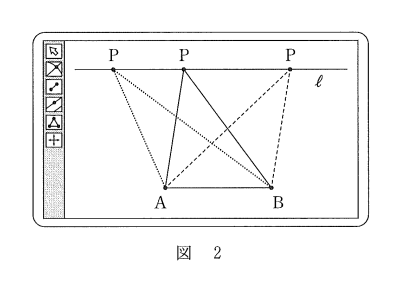
(2) 太郎さんは、図2のように、問題1の点 P のとり方に条件を付けて、次の問題2を考えた。
問題2
直線 AB に平行な直線を $\ell$ とし、直線 $\ell$ 上で点 P をいろいろな位置にとる。このとき、外接円の半径 $R$ が最小となる $\triangle \mathrm{ ABP }$ はどのような三角形か。
太郎さんは、この問題を解決するために、次の構想を立てた。
問題2の解決の構想
問題1の考察から、線分 AB を直径とする円を C とし、円 C に着目する。直線 $\ell$ は、その位置によって、円 C と共有点をもつ場合ともたない場合があるので、それぞれの場合に分けて考える。直線 AB と直線 $\ell$ との距離を $h$ とする。直線 $\ell$ が円 C と共有点をもつ場合は、 $h\leqq \myBox{サ}$ のときであり、共有点をもたない場合は、 $h\gt \mybox{サ}$ のときである。
(i) $h\leqq \mybox{サ}$ のとき
直線 $\ell$ が円 C と共有点をもつので、 $R$ が最小となる $\triangle \mathrm{ ABP }$ は、 $h\lt \mybox{サ}$ のとき $\dBox{シ}$ であり、 $h=\mybox{サ}$ のとき直角二等辺三角形である。
(ii) $h\gt\mybox{サ}$ のとき
線分 AB の垂直二等分線を $m$ とし、直線 $m$ と直線 $\ell$ との交点を $\mathrm{P}_1$ とする。直線 $\ell$ 上にあり点 $\mathrm{P}_1$ とは異なる点を $\mathrm{P}_2$ とするとき $\sin\angle\mathrm{AP_1B}$ と $\sin\angle\mathrm{AP_2B}$ の大小を考える。$\triangle \mathrm{ABP_2}$ の外接円と直線 $m$ との共有点のうち、直線 AB に関して点 $\mathrm{P}_2$ と同じ側にある点を $\mathrm{P}_3$ とすると、 $\angle \mathrm{AP_3B}\ \dBox{ス}\ \angle \mathrm{AP_2B}$ である。また、 $\angle \mathrm{AP_3B}\lt\angle \mathrm{AP_1B}\lt90^{\circ}$ より $\sin\angle \mathrm{AP_3B}\ \dBox{セ}\ \sin\angle\mathrm{AP_1B}$ である。このとき
($\triangle \mathrm{ABP_1}$ の外接円の半径) $\dBox{ソ}$ ($\triangle \mathrm{ABP_2}$ の外接円の半径)
であり、 $R$ が最小となる $\triangle \mathrm{ABP}$ は $\dBox{タ}$ である。
$\dbox{シ}$ , $\dbox{タ}$ については、最も適当なものを、次の 0 ~ 4 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: 鈍角三角形
1: 直角三角形
2: 正三角形
3: 二等辺三角形
4: 直角二等辺三角形
$\dbox{ス}$ ~ $\dbox{ソ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\lt$
1: $=$
2: $\gt$
(3) 問題2の考察を振り返って、 $h=8$ のとき、 $\triangle \mathrm{ ABP }$ の外接円の半径 $R$ が最小である場合について考える。このとき、 $\sin\angle \mathrm{ APB }=\dfrac{\myBox{チ} }{\myBox{ツ} }$ であり、 $R=\myBox{テ}$ である。
考え方
正弦定理を用いて、外接円の半径が最小になる場合を考える問題です。単純に値を出すだけでなく、角度に応じて正弦の値がどう変わり、外接円の半径がどう変わるのかを考えなくてはいけません。図を正しくかきながら考える必要もあります。計算自体はほとんどありません。
解答編
問題
平面上に2点 A, B があり、 $\mathrm{AB}=8$ である。直線 AB 上にない点 P をとり、 $\triangle \mathrm{ ABP }$ をつくり、その外接円の半径を $R$ とする。
太郎さんは、図1のように、コンピュータソフトを使って点 P をいろいろな位置にとった。
図1は、点 P をいろいろな位置にとったときの $\triangle \mathrm{ ABP }$ の外接円をかいたものである。
(1) 太郎さんは、点 P のとり方によって外接円の半径が異なることに気づき、次の問題1を考えることにした。
問題1
点 P をいろいろな位置にとるとき、外接円の半径 $R$ が最小となる $\triangle \mathrm{ ABP }$ はどのような三角形か。正弦定理により、 $2R=\dfrac{\myBox{キ} }{\sin\angle \mathrm{ APB } }$ である。よって、 $R$ が最小となるのは $\angle \mathrm{ APB }=\myBox{クケ}^{\ \circ}$ の三角形である。このとき、 $R=\myBox{コ}$ である。
解説
正弦定理より\[ 2R=\frac{\mathrm{ AB } }{\sin\angle \mathrm{ APB } } =\frac{8}{\sin\angle \mathrm{ APB } } \]となります。
$R$ が最小となるのは、右辺が最小となるときであり、分母が正であることから分母が最大のときです。つまり、 $\angle \mathrm{ APB }=90^{\circ}$ のときです。このとき、 $2R=8$ なので、 $R=4$ です。
解答
キ:8
クケ:90
コ:4
解答編 つづき
(2) 太郎さんは、図2のように、問題1の点 P のとり方に条件を付けて、次の問題2を考えた。
問題2
直線 AB に平行な直線を $\ell$ とし、直線 $\ell$ 上で点 P をいろいろな位置にとる。このとき、外接円の半径 $R$ が最小となる $\triangle \mathrm{ ABP }$ はどのような三角形か。
太郎さんは、この問題を解決するために、次の構想を立てた。
問題2の解決の構想
問題1の考察から、線分 AB を直径とする円を C とし、円 C に着目する。直線 $\ell$ は、その位置によって、円 C と共有点をもつ場合ともたない場合があるので、それぞれの場合に分けて考える。直線 AB と直線 $\ell$ との距離を $h$ とする。直線 $\ell$ が円 C と共有点をもつ場合は、 $h\leqq \myBox{サ}$ のときであり、共有点をもたない場合は、 $h\gt \mybox{サ}$ のときである。
解説
円 C が直線 $\ell$ と共有点を持つのは、円の中心から直線までの距離が半径以下となるときです。
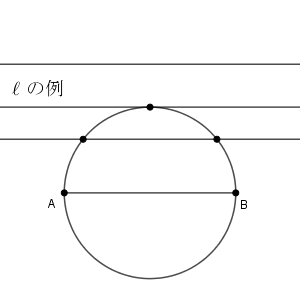
半径は線分 AB の長さの半分なので $4$ です。これより、 $h\leqq 4$ のときに共有点をもち、 $h\gt 4$ のときに共有点をもたないことがわかります。
解答
サ:4
解答編 つづき
(i) $h\leqq \mybox{サ}$ のとき
直線 $\ell$ が円 C と共有点をもつので、 $R$ が最小となる $\triangle \mathrm{ ABP }$ は、 $h\lt \mybox{サ}$ のとき $\dBox{シ}$ であり、 $h=\mybox{サ}$ のとき直角二等辺三角形である。
(ii) $h\gt\mybox{サ}$ のとき
線分 AB の垂直二等分線を $m$ とし、直線 $m$ と直線 $\ell$ との交点を $\mathrm{P}_1$ とする。直線 $\ell$ 上にあり点 $\mathrm{P}_1$ とは異なる点を $\mathrm{P}_2$ とするとき $\sin\angle\mathrm{AP_1B}$ と $\sin\angle\mathrm{AP_2B}$ の大小を考える。$\triangle \mathrm{ABP_2}$ の外接円と直線 $m$ との共有点のうち、直線 AB に関して点 $\mathrm{P}_2$ と同じ側にある点を $\mathrm{P}_3$ とすると、 $\angle \mathrm{AP_3B}\ \dBox{ス}\ \angle \mathrm{AP_2B}$ である。また、 $\angle \mathrm{AP_3B}\lt\angle \mathrm{AP_1B}\lt90^{\circ}$ より $\sin\angle \mathrm{AP_3B}\ \dBox{セ}\ \sin\angle\mathrm{AP_1B}$ である。このとき
($\triangle \mathrm{ABP_1}$ の外接円の半径) $\dBox{ソ}$ ($\triangle \mathrm{ABP_2}$ の外接円の半径)
であり、 $R$ が最小となる $\triangle \mathrm{ABP}$ は $\dBox{タ}$ である。
$\dbox{シ}$ , $\dbox{タ}$ については、最も適当なものを、次の 0 ~ 4 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: 鈍角三角形
1: 直角三角形
2: 正三角形
3: 二等辺三角形
4: 直角二等辺三角形
$\dbox{ス}$ ~ $\dbox{ソ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\lt$
1: $=$
2: $\gt$
解説
$h\leqq 4$ の場合は、円 C と直線 $\ell$ は共有点をもちます。
$2R=\dfrac{8}{\sin\angle \mathrm{ APB } }$ なので、分母が一番大きくなるときを考えると、 $\angle\mathrm{APB}=90^{\circ}$ のときです。円 C と直線 $\ell$ が共有点を持つ場合は、その共有点を点 P として選べばいいです。
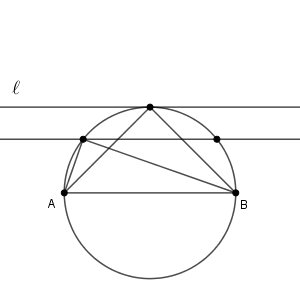
$h\lt 4$ のときは直角三角形、 $h=4$ のときは直角二等辺三角形となります。
一方、 $h\gt 4$ の場合は、円と直線 $\ell$ とは共有点を持ちません。このときに、問題文にあるように点 $\mathrm{P}_1$, $\mathrm{P}_2$, $\mathrm{P}_3$ をとって考えます。
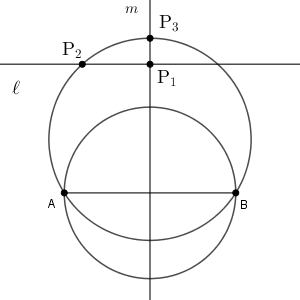
点 $\mathrm{P}_2$, $\mathrm{P}_3$ は $\triangle \mathrm{ ABP_2 }$ の外接円上の点なので、円周角の定理から $\angle \mathrm{AP_3B}=\angle \mathrm{AP_2B}$ となります。また、 $\angle \mathrm{AP_3B}\lt\angle \mathrm{AP_1B}\lt 90^{\circ}$ なので、 $\sin\angle \mathrm{AP_3B} \lt \sin\angle\mathrm{AP_1B}$ となります。
以上から、 $\ell$ 上に点 P をとり、 $\sin\angle \mathrm{ APB }$ が最大になるのは、 $\angle\mathrm{APB}$ が最大になるときであり、 $\mathrm{ P_1 }$ のときであることがわかります。このときに外接円の半径は最小となり、 $\triangle \mathrm{ ABP }$ は二等辺三角形となります。
解答
シ:1
ス:1
セ:0
ソ:0
タ:3
解答編 つづき
(3) 問題2の考察を振り返って、 $h=8$ のとき、 $\triangle \mathrm{ ABP }$ の外接円の半径 $R$ が最小である場合について考える。このとき、 $\sin\angle \mathrm{ APB }=\dfrac{\myBox{チ} }{\myBox{ツ} }$ であり、 $R=\myBox{テ}$ である。
解説
(2)で見たことから、 $h=8\gt 4$ の場合は、次のような二等辺三角形のときに $R$ が最小となります。
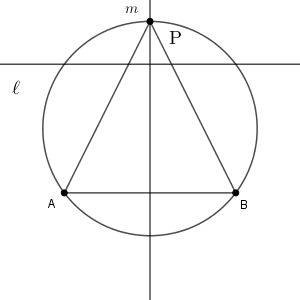
このとき、 $\mathrm{AP}=\mathrm{BP}=\sqrt{8^2+4^2}=4\sqrt{5}$ なので、正弦定理から
\begin{eqnarray}
\frac{\mathrm{ BP } }{\sin\angle\mathrm{ PAB } } &=& \frac{\mathrm{ AB } }{\sin\angle\mathrm{ APB } } \\[5pt]
\frac{4\sqrt{5} }{\frac{8}{4\sqrt{5} }} &=& \frac{8}{\sin\angle\mathrm{ APB } } \\[5pt]
10 &=& \frac{8}{\sin\angle\mathrm{ APB } } \\[5pt]
\sin\angle\mathrm{ APB } &=& \frac{4}{5} \\[5pt]
\end{eqnarray}となることがわかります。また、\[ 2R=\frac{BP}{\sin\angle\mathrm{ PAB } }=10 \]なので、 $R=5$ です。
解答
チツ:45
テ:5