共通テスト 数学I・数学A 2018年度プレテスト 第1問 [4] 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
三角形 ABC の外接円を O とし、円O の半径を R とする。辺BC、CA、 AB の長さをそれぞれ $a,b,c$ とし、 $\angle \mathrm{CAB}$, $\angle \mathrm{ABC}$, $\angle \mathrm{BCA}$ の大きさをそれぞれ $A,B,C$ とする。
太郎さんと花子さんは三角形 ABC について\[ \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R \ \cdots(*) \]の関係が成り立つことを知り、その理由について、まず直角三角形の場合を次のように考察した。
$C=90^{\circ}$ のとき、円周角の定理より、線分 AB は円O の直径である。
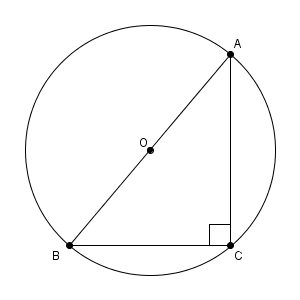
よって、\[ \sin A=\frac{\mathrm{ BC } }{\mathrm{ AB } }=\frac{a}{2R} \]であるから、\[ \frac{a}{\sin A}=2R \]となる。
同様にして、\[ \frac{b}{\sin B}=2R \]である。
また、$\sin C=1$ なので、\[ \frac{c}{\sin C}=\mathrm{ AB }=2R \]である。
よって、 $C= 90^{\circ}$ のとき (*) の関係が成り立つ。次に、太郎さんと花子さんは、三角形 ABC が鋭角三角形や鈍角三角形のときにも (*) の関係が成り立つことを証明しようとしている。
(1) 三角形 ABC が鋭角三角形の場合についても (*) の関係が成り立つことは、直角三角形の場合に (*) の関係が成り立つことをもとにして、次のような太郎さんの構想により証明できる。
【太郎さんの証明の構想】
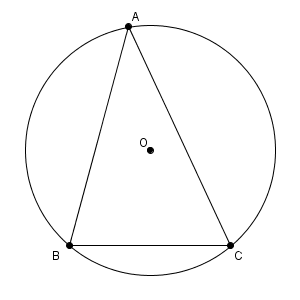
点 A を含む弧 BC 上に点 $\mathrm{A}'$ をとると、円周角の定理より\[ \angle \mathrm{CAB}=\angle\mathrm{CA'B} \]が成り立つ。
特に、 $\myBox{カ}$ を点 $\mathrm{A}'$ とし、三角形 $\mathrm{A'BC}$ に対して $C=90^{\circ}$ の場合の考察の結果を利用すれば、\[ \frac{a}{\sin A}=2R \]が成り立つことを証明できる。
$\dfrac{b}{\sin B}=2R$, $\dfrac{c}{\sin C}=2R$ についても同様に証明できる。$\myBox{カ}$ に当てはまる最も適当なものを、次の 0~4 のうちから一つ選べ。
0: 点 B から辺 AC に下ろした垂線と、円O との交点のうち点B と異なる点
1: 直線 BO と円O との交点のうち点B と異なる点
2: 点B を中心とし点C を通る円と、円O との交点のうち点C と異なる点
3: 点 O を通り辺 BC に平行な直線と、円O との交点のうちの一つ
4: 辺 BC と直交する円O の直径と、円O との交点のうちの一つ
(2) 三角形 ABC が $A \gt 90^{\circ}$ である鈍角三角形の場合についても $\dfrac{a}{\sin A}=2R$ が成り立つことは、次のような花子きんの構想により証明できる。
【花子さんの証明の構想】
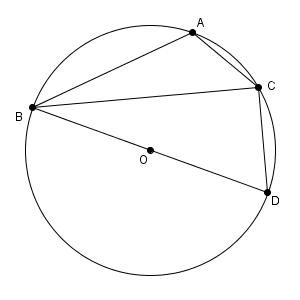
右図のように、線分 BD が円O の直径となるように点D をとると、三角形 BCD において\[ \sin \myBox{キ}=\frac{a}{2R} \]である。
このとき、四角形 ABDC は円O に内接するから、\[ \angle \mathrm{ CAB }=\myBox{ク} \]であり、\[ \sin\angle\mathrm{ CAB }=\sin\left(\mybox{ク}\right) =\sin\mybox{キ} \]となることを用いる。$\myBox{キ}$, $\myBox{ク}$ に当てはまるものを、次の各解答群のうちから一つずつ選べ。
$\myBox{キ}$ の解答群
0: $\angle \mathrm{ ABC }$
1: $\angle \mathrm{ ABD }$
2: $\angle \mathrm{ ACB }$
3: $\angle \mathrm{ ACD }$4: $\angle \mathrm{ BCD }$
5: $\angle \mathrm{ BDC }$
6: $\angle \mathrm{ CBD }$$\myBox{ク}$ の解答群
0: $90^{\circ} +\angle \mathrm{ ABC }$
1: $180^{\circ}-\angle \mathrm{ ABC }$2: $90^{\circ} +\angle \mathrm{ ACB}$
3: $180^{\circ}-\angle \mathrm{ ACB }$4: $90^{\circ} +\angle \mathrm{ BDC }$
5: $180^{\circ}-\angle \mathrm{ BDC }$6: $90^{\circ} +\angle \mathrm{ ABD }$
7: $180^{\circ}-\angle \mathrm{ CBD }$
考え方
正弦定理の証明です。教科書に載っている証明がそのまま出題されています。(参考:【基本】正弦定理の証明)
正弦定理を使った問題演習はたくさんしているでしょうが、定理の証明自体はあまり何度も見ないかもしれません。そういう、「応用はできるけど、なぜそれが成り立つかをおろそかにしてしまってないか」を問う問題となっています。
【必答問題】
解答編
問題
三角形 ABC の外接円を O とし、円O の半径を R とする。辺BC、CA、 AB の長さをそれぞれ $a,b,c$ とし、 $\angle \mathrm{CAB}$, $\angle \mathrm{ABC}$, $\angle \mathrm{BCA}$ の大きさをそれぞれ $A,B,C$ とする。
太郎さんと花子さんは三角形 ABC について\[ \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R \ \cdots(*) \]の関係が成り立つことを知り、その理由について、まず直角三角形の場合を次のように考察した。
$C=90^{\circ}$ のとき、円周角の定理より、線分 AB は円O の直径である。

よって、\[ \sin A=\frac{\mathrm{ BC } }{\mathrm{ AB } }=\frac{a}{2R} \]であるから、\[ \frac{a}{\sin A}=2R \]となる。
同様にして、\[ \frac{b}{\sin B}=2R \]である。
また、$\sin C=1$ なので、\[ \frac{c}{\sin C}=\mathrm{ AB }=2R \]である。
よって、 $C= 90^{\circ}$ のとき (*) の関係が成り立つ。次に、太郎さんと花子さんは、三角形 ABC が鋭角三角形や鈍角三角形のときにも (*) の関係が成り立つことを証明しようとしている。
解説
とても長い前フリです。正弦定理の証明のうち、一番特殊で考えやすい、直角三角形の場合ですね。これは、そのまま読むだけです。
解答編 つづき
問題
(1) 三角形 ABC が鋭角三角形の場合についても (*) の関係が成り立つことは、直角三角形の場合に (*) の関係が成り立つことをもとにして、次のような太郎さんの構想により証明できる。
【太郎さんの証明の構想】

点 A を含む弧 BC 上に点 $\mathrm{A}'$ をとると、円周角の定理より\[ \angle \mathrm{CAB}=\angle\mathrm{CA'B} \]が成り立つ。
特に、 $\myBox{カ}$ を点 $\mathrm{A}'$ とし、三角形 $\mathrm{A'BC}$ に対して $C=90^{\circ}$ の場合の考察の結果を利用すれば、\[ \frac{a}{\sin A}=2R \]が成り立つことを証明できる。
$\dfrac{b}{\sin B}=2R$, $\dfrac{c}{\sin C}=2R$ についても同様に証明できる。$\myBox{カ}$ に当てはまる最も適当なものを、次の 0~4 のうちから一つ選べ。
0: 点 B から辺 AC に下ろした垂線と、円O との交点のうち点B と異なる点
1: 直線 BO と円O との交点のうち点B と異なる点
2: 点B を中心とし点C を通る円と、円O との交点のうち点C と異なる点
3: 点 O を通り辺 BC に平行な直線と、円O との交点のうちの一つ
4: 辺 BC と直交する円O の直径と、円O との交点のうちの一つ
解説
鋭角三角形に対して正弦定理の証明をするには、直角三角形の場合に帰着させます。
問題文中にもある通り、 $C=90^{\circ}$ の場合に考えていたことを使いたいのだから、次のように $\mathrm{A}'$ をとるのが自然です。
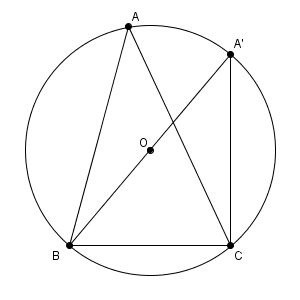
こうすると、直角三角形のときで見たように\[ \frac{a}{\sin\angle\mathrm{CA'B} }=2R \]が成り立ちます。また、問題文中にあるように、円周角の定理から、左辺の分母は $\sin A$ と等しいことがわかるから、このときも\[ \frac{a}{\sin A}=2R \]が成り立つことが示せます。
このような $\mathrm{A}'$ をとればいいので、この点の説明として一番適当なものは、1の「直線BO と円O との交点のうち点B と異なる点」であることがわかります。
解答
カ:1
解答編 つづき
問題
(2) 三角形 ABC が $A \gt 90^{\circ}$ である鈍角三角形の場合についても $\dfrac{a}{\sin A}=2R$ が成り立つことは、次のような花子きんの構想により証明できる。
【花子さんの証明の構想】

右図のように、線分 BD が円O の直径となるように点D をとると、三角形 BCD において\[ \sin \myBox{キ}=\frac{a}{2R} \]である。
このとき、四角形 ABDC は円O に内接するから、\[ \angle \mathrm{ CAB }=\myBox{ク} \]であり、\[ \sin\angle\mathrm{ CAB }=\sin\left(\mybox{ク}\right) =\sin\mybox{キ} \]となることを用いる。$\myBox{キ}$, $\myBox{ク}$ に当てはまるものを、次の各解答群のうちから一つずつ選べ。
$\myBox{キ}$ の解答群
0: $\angle \mathrm{ ABC }$
1: $\angle \mathrm{ ABD }$
2: $\angle \mathrm{ ACB }$
3: $\angle \mathrm{ ACD }$4: $\angle \mathrm{ BCD }$
5: $\angle \mathrm{ BDC }$
6: $\angle \mathrm{ CBD }$$\myBox{ク}$ の解答群
0: $90^{\circ} +\angle \mathrm{ ABC }$
1: $180^{\circ}-\angle \mathrm{ ABC }$2: $90^{\circ} +\angle \mathrm{ ACB}$
3: $180^{\circ}-\angle \mathrm{ ACB }$4: $90^{\circ} +\angle \mathrm{ BDC }$
5: $180^{\circ}-\angle \mathrm{ BDC }$6: $90^{\circ} +\angle \mathrm{ ABD }$
7: $180^{\circ}-\angle \mathrm{ CBD }$
解説

三角形 BCD は直角三角形だから、冒頭の結果が使えます。辺の長さ $a$ が出てくるようにするには、角度を $\angle \mathrm{ BDC }$ にすればいいですね。
また、円に内接する四角形については、向かい合う内角の和が180度なので、\[ \angle \mathrm{ CAB }=180^{\circ}-\angle \mathrm{ BDC } \]となります。
一般に、 $\sin \theta$ と $\sin(180^{\circ}-\theta)$ の値は等しくなる(参考:【基本】補角の三角比)ので、結局、鈍角三角形の場合にも、\[ \frac{a}{\sin A}=2R \]が成り立つことが示せます。
解答
キ:5
ク:5





