共通テスト数学I・数学A 2018年度プレテスト第1問 [3] 解説

🕒 2018/11/11 🔄 2023/05/03

2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【必答問題】

問題編

問題

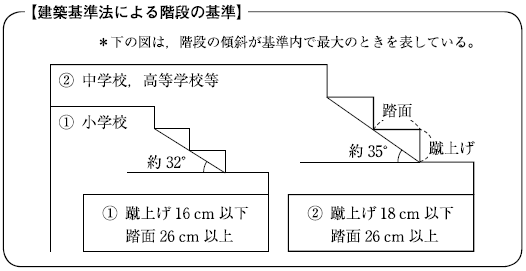
　久しぶりに小学校に行くと、階段の一段一段の高さが低く感じられることがある。これは、小学校と高等学校とでは階段の基準が異なるからである。学校の階段の基準は、下のように建築基準法によって定められている。

　高等学校の階段では、蹴上げ（けあげ）が 18cm 以下、踏面（ふみづら）が 26cm 以上となっており、この基準では、傾斜は最大で約 35°である。

　階段の傾斜をちょうど 33°とするとき、蹴上げを 18cm 以下にするためには、踏面をどのような範囲に設定すればよいか。踏面を $x$ cm として、 $x$ のとり得る値の範囲を求めるための不等式を、33°の三角比と $x$ を用いて表せ。解答は、解答欄 $\myBox{(い)}$ に記述せよ。ただし踏面と蹴上げの長さはそれぞれ一定であるとし、また、踏面は水平であり、蹴上げは踏面に対して垂直であるとする。

(本問題の図は、「建築基準法の階段に係る基準について」(国土交通省)をもとに作成している。)

考え方

はじめて見る用語が出てきますが、図があるので意味は分かるでしょう。

「蹴上げを 18cm以下にする」という条件を、 $x$ を使った式で表せばいいですね。上限だけでなく、下限もあることに注意しましょう。問題文をよく読まないと、下限をミスしてしまうかもしれません（そこは数学の問題ではない気がしますが）。

【必答問題】

解答編

問題

　久しぶりに小学校に行くと、階段の一段一段の高さが低く感じられることがある。これは、小学校と高等学校とでは階段の基準が異なるからである。学校の階段の基準は、下のように建築基準法によって定められている。

　高等学校の階段では、蹴上げ（けあげ）が 18cm 以下、踏面（ふみづら）が 26cm 以上となっており、この基準では、傾斜は最大で約 35°である。

　階段の傾斜をちょうど 33°とするとき、蹴上げを 18cm 以下にするためには、踏面をどのような範囲に設定すればよいか。踏面を $x$ cm として、 $x$ のとり得る値の範囲を求めるための不等式を、33°の三角比と $x$ を用いて表せ。解答は、解答欄 $\myBox{(い)}$ に記述せよ。ただし踏面と蹴上げの長さはそれぞれ一定であるとし、また、踏面は水平であり、蹴上げは踏面に対して垂直であるとする。

(本問題の図は、「建築基準法の階段に係る基準について」(国土交通省)をもとに作成している。)

解説

蹴上げを 18cm 以下にする、という不等式を、 $x$ を使って表してみましょう。階段の傾斜は、「蹴上げ÷踏面」で求められ、この角度が 33°なのだから、蹴上げは、\[ x\tan 33^{\circ} \]で表すことができます。これが 18cm以下となるようにするには、\[ x\leqq \frac{18}{\tan 33^{\circ} } \]を満たせばいいですね。

踏面は、26cm 以上という条件があるので、\[ 26\leqq x \leqq \frac{18}{\tan 33^{\circ} } \]が $x$ のとり得る値の範囲となります。下限は0ではありません。