共通テスト数学I・数学A 2018年度プレテスト第3問解説

🕒 2018/11/14 🔄 2023/05/01

2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【選択問題】(第3問～第5問から2問選択)

問題編

問題

　くじが 100本ずつ入った二つの箱があり、それぞれの箱に入っている当たりくじの本数は異なる。これらの箱から二人の人が順にどちらかの箱を選んで 1本ずつくじを引く。ただし、引いたくじはもとに戻さないものとする。

　また、くじを引く人は、最初にそれぞれの箱に入れる当たりくじの本数は知っているが、それらがどちらの箱に入っているかはわからないものとする。

　今、1番目の人が一方の箱からくじを 1本引いたところ、当たりくじであったとする。2番目の人が当たりくじを引く確率を大きくするためには、1番目の人が引いた箱と同じ箱、異なる箱のどちらを選ぶべきかを考察しよう。

　最初に当たりくじが多く入っている方の箱を A、もう一方の箱を B とし. 1番目の人がくじを引いた箱が A である事象を $A$ 、B である事象を $B$ とする。このとき、 $P(A)=P(B)=\dfrac{1}{2}$ とする。また、 1番目の人が当たりくじを引く事象を $W$ とする。

　太郎さんと花子さんは、箱A、箱B に入っている当たりくじの本数によって、2 番目の人が当たりくじを引く確率がどのようになるかを調べている。

(1) 箱 A には当たりくじが 10 本入っていて箱 B には当たりくじが 5 本入っている場合を考える。

1番目の人が当たりくじを引いたから、その箱が箱 A である可能性が高そうだね。その場合、箱 A には当たりくじが 9 本残っているから、2番目の人は、1番目の人と同じ箱からくじを引いた方がよさそうだよ。

確率を計算してみようよ。

　1 番目の人が引いた箱が箱 A で、かつ当たりくじを引く確率は、\[ P(A\cap W)=P(A)\cdot P_A(W)=\dfrac{\myBox{ア} }{\myBox{イウ} } \]である。一方で、1番目の人が当たりくじを引く事象 $W$ は、箱 A から当たりくじを引くか箱 B から当たりくじを引くかのいずれかであるので、その確率は、\[ P(W) = \dfrac{\myBox{エ} }{\myBox{オカ} } \]である。

　よって、1番目の人が当たりくじを引いたという条件の下で、その箱が箱 A であるという条件付き確率 $P_W(A)$ は、\[ P_W(A)=\frac{P(A\cap W)}{P(W)}=\dfrac{\myBox{キ} }{\myBox{ク} } \]と求められる。

　また、1番目の人が当たりくじを引いた後、同じ箱から 2 番目の人がくじを引くとき、そのくじが当たりくじである確率は、\[ P_W(A)\times\frac{9}{99}+P_W(B)\times\dfrac{\myBox{ケ} }{99}=\dfrac{\myBox{コ} }{\myBox{サシ} } \]である。

　それに対して. 1番目の人が当たりくじを引いた後、異なる箱から 2 番目の人がくじを引くとき、そのくじが当たりくじである確率は、 $\dfrac{\myBox{ス} }{\myBox{セソ} }$ である。

やっぱり 1番目の人が当たりくじを引いた場合は、同じ箱から引いた方が当たりくじを引く確率が大きいよ。

そうだね。でも、思ったより確率の差はないんだね。もう少し当たりくじの本数の差が小さかったらどうなるのだろう。

1番目の人が引いた箱が箱 A の可能性が高いから、箱 B の当たりくじの本数が 8本以下だったら、同じ箱のくじを引いた方がよいのではないかな。

確率を計算してみようよ。

(2) 今度は箱 A には当たりくじが 10 本入っていて、箱 B には当たりくじが 7本入っている場合を考える。

　1番目の人が当たりくじを引いた後、同じ箱から 2 番目の人がくじを引くとき、そのくじが当たりくじである確率は $\dfrac{\myBox{タ} }{\myBox{チツ} }$ である。それに対して異なる箱からくじを引くとき、そのくじが当たりくじである確率は $\dfrac{7}{85}$ である。

今度は異なる箱から引く方が当たりくじを引く確率が大きくなったね。

最初に当たりくじを引いた箱の方が箱 A である確率が大きいのに不思議だね。計算してみないと直観ではわからなかったな。

二つの箱に入っている当たりくじの本数の差が小さくなれば、最初に当たりくじを引いた箱が A である確率と B である確率の差も小さくなるよ。最初に当たりくじを引いた箱がB である場合は、もともと当たりくじが少ない上に前の人がl 本引いてしまっているから当たりくじはなおさら引きにくいね。

なるほどね。箱 A に入っている当たりくじの本数は 10 本として、箱 B に入っている当たりくじが何本であれば同じ箱から引く方がよいのかを調べてみよう。

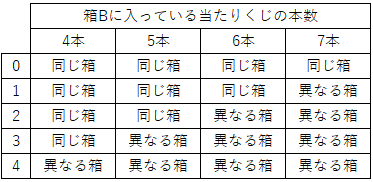
(3) 箱 A に当たりくじが 10 本入っている場合、1 番目の人が当たりくじを引いたとき、2番目の人が当たりくじを引く確率を大きくするためには、1番目の人が引いた箱と同じ箱、異なる箱のどちらを選ぶべきか。箱 B に入っている当たりくじの本数が 4 本、5 本、6 本、7 本のそれぞれの場合において選ぶべき箱の組み合わせとして正しいものを、次の 0～4 のうちから一つ選べ。 $\myBox{テ}$

考え方

多くの人が苦手とする条件付き確率がオンパレードです。結果からさかのぼるタイプの条件付き確率なので、苦手とする人も多いでしょう。

ただ、(1)では、丁寧に誘導がついていて、それを(2)(3)で繰り返すだけです。(2)では、ヒントもあるし、(3)では、問題文から選択肢を絞ることもできますが、まじめにやると結構時間がかかってしまいます。

【選択問題】(第3問～第5問から2問選択)

解答編

問題

　くじが 100本ずつ入った二つの箱があり、それぞれの箱に入っている当たりくじの本数は異なる。これらの箱から二人の人が順にどちらかの箱を選んで 1本ずつくじを引く。ただし、引いたくじはもとに戻さないものとする。

　また、くじを引く人は、最初にそれぞれの箱に入れる当たりくじの本数は知っているが、それらがどちらの箱に入っているかはわからないものとする。

　今、1番目の人が一方の箱からくじを 1本引いたところ、当たりくじであったとする。2番目の人が当たりくじを引く確率を大きくするためには、1番目の人が引いた箱と同じ箱、異なる箱のどちらを選ぶべきかを考察しよう。

　最初に当たりくじが多く入っている方の箱を A、もう一方の箱を B とし. 1番目の人がくじを引いた箱が A である事象を $A$ 、B である事象を $B$ とする。このとき、 $P(A)=P(B)=\dfrac{1}{2}$ とする。また、 1番目の人が当たりくじを引く事象を $W$ とする。

　太郎さんと花子さんは、箱A、箱B に入っている当たりくじの本数によって、2 番目の人が当たりくじを引く確率がどのようになるかを調べている。

(1) 箱 A には当たりくじが 10 本入っていて箱 B には当たりくじが 5 本入っている場合を考える。

1番目の人が当たりくじを引いたから、その箱が箱 A である可能性が高そうだね。その場合、箱 A には当たりくじが 9 本残っているから、2番目の人は、1番目の人と同じ箱からくじを引いた方がよさそうだよ。

確率を計算してみようよ。

　1 番目の人が引いた箱が箱 A で、かつ当たりくじを引く確率は、\[ P(A\cap W)=P(A)\cdot P_A(W)=\dfrac{\myBox{ア} }{\myBox{イウ} } \]である。

解説

1番目の人がひいた箱が箱Aで、かつ、当たりくじを引く確率を考えましょう。箱を選んだときに、Aの箱かBの箱か、確率は $\dfrac{1}{2}$ だと、問題文中にありますね。また、Aの箱には当たりくじが10本あります。この2つを掛ければいいので、求める確率は、\[ \frac{1}{2}\times \frac{10}{100}=\frac{1}{20} \]となります。

解答

アイウ：120

解答編つづき

問題

一方で、1番目の人が当たりくじを引く事象 $W$ は、箱 A から当たりくじを引くか箱 B から当たりくじを引くかのいずれかであるので、その確率は、\[ P(W) = \dfrac{\myBox{エ} }{\myBox{オカ} } \]である。

解説

1番目の人が当たりをひく事象は、箱Aから当たりを引くか、箱Bから当たりを引くか、のどちらかで、両者にダブりはありません。なので、2つの確率を足せば答えです。前者は先ほど求めた通り、 $\dfrac{1}{20}$ です。後者は、箱Bを選び、かつ当たりを引く確率を計算すればいいので、先ほどと同様にすると\[ \frac{1}{2}\times\frac{5}{100}=\frac{1}{40} \]となります。

よって、1番目の人が当たりくじを引く確率は、\[ \frac{1}{20}+\frac{1}{40}=\frac{3}{40} \]となります。

解答

エオカ：340

解答編つづき

問題

　よって、1番目の人が当たりくじを引いたという条件の下で、その箱が箱 A であるという条件付き確率 $P_W(A)$ は、\[ P_W(A)=\frac{P(A\cap W)}{P(W)}=\dfrac{\myBox{キ} }{\myBox{ク} } \]と求められる。

解説

条件付き確率の問題です。どちらかというと、原因の確率に分類されるものですが、計算式も書いてくれているので、難しくはないでしょう。

条件付き確率というのは、世界を限定して考えることになります。ここでは、「1番目の人が当たりを引いた」という世界で考えることになります。なので、分母は、「1番目の人が当たりを引いた確率」となります。その世界で、「箱Aから当たりを引いていた確率」を考えるわけですね。そのため、分子は「1番目の人が、箱Aから当たりを引いた確率」となります。

それぞれの確率はすでに計算しているので、\[ P_W(A)=\frac{\frac{1}{20} }{\frac{3}{40} }=\frac{2}{3} \]となります。

解答

キク：23

解答編つづき

問題

　また、1番目の人が当たりくじを引いた後、同じ箱から 2 番目の人がくじを引くとき、そのくじが当たりくじである確率は、\[ P_W(A)\times\frac{9}{99}+P_W(B)\times\dfrac{\myBox{ケ} }{99}=\dfrac{\myBox{コ} }{\myBox{サシ} } \]である。

　それに対して. 1番目の人が当たりくじを引いた後、異なる箱から 2 番目の人がくじを引くとき、そのくじが当たりくじである確率は、 $\dfrac{\myBox{ス} }{\myBox{セソ} }$ である。

解説

1番目の人が当たりくじを引いた後、同じ箱から2番目の人も当たる確率は、2人とも箱Aから引いたときと、2人とも箱Bから引いたときの2つの場合があり、両者にはダブりはありません。なので、それぞれを足せばいいですね。

箱Aの場合は、2人目が引くときには、99本のくじの中にあたりが9本あります。箱Bの場合は、4本です。なので、
\begin{eqnarray} & & P_W(A)\times \frac{9}{99}+P_W(B)\times \frac{4}{99} \\[5pt] \end{eqnarray}を計算することになります。Aさんが当たっているときに、それが箱Aである確率は、先ほど計算した通り、 $\dfrac{2}{3}$ でした。よって、箱Bである確率は $\dfrac{1}{3}$ です。よって、2人とも当たる確率は \begin{eqnarray} & & \frac{2}{3}\times \frac{9}{99}+\frac{1}{3}\times \frac{4}{99} \\[5pt] &=& \frac{2\times9+4}{3\times 99} \\[5pt] &=& \frac{22}{3\times 99} \\[5pt] &=& \frac{2}{27} \\[5pt] \end{eqnarray}となります。

次に、1番目の人が当たっていて、2番目の人は異なる箱から当たりを引く確率を計算しましょう。異なる箱は、全体のくじも当たりくじも、数ははじめの状態から変わっていないので
\begin{eqnarray} & & \frac{2}{3}\times \frac{5}{100}+\frac{1}{3}\times \frac{10}{100} \\[5pt] &=& \frac{2\times5+10}{3\times 100} \\[5pt] &=& \frac{20}{3\times 100} \\[5pt] &=& \frac{1}{15} \\[5pt] \end{eqnarray}となります。

両者を比較すると、 $\dfrac{2}{27}=\dfrac{10}{105}$ と $\dfrac{1}{15}=\dfrac{7}{105}$ となり、前者、つまり、同じ箱を選ぶ方が確率が高くなることがわかります。

解答

ケ：4
コサシ：227
スセソ：115

解答編つづき

問題

やっぱり 1番目の人が当たりくじを引いた場合は、同じ箱から引いた方が当たりくじを引く確率が大きいよ。

そうだね。でも、思ったより確率の差はないんだね。もう少し当たりくじの本数の差が小さかったらどうなるのだろう。

1番目の人が引いた箱が箱 A の可能性が高いから、箱 B の当たりくじの本数が 8本以下だったら、同じ箱のくじを引いた方がよいのではないかな。

確率を計算してみようよ。

(2) 今度は箱 A には当たりくじが 10 本入っていて、箱 B には当たりくじが 7本入っている場合を考える。

　1番目の人が当たりくじを引いた後、同じ箱から 2 番目の人がくじを引くとき、そのくじが当たりくじである確率は $\dfrac{\myBox{タ} }{\myBox{チツ} }$ である。それに対して異なる箱からくじを引くとき、そのくじが当たりくじである確率は $\dfrac{7}{85}$ である。

解説

先ほどの計算で、5本のところを7本に変えて計算しましょう。

まず、1番目の人が当たる確率を、箱Aから引くか、箱Bから引くかで場合分けをして考えると、
\begin{eqnarray} \frac{1}{2}\cdot\frac{10}{100}+\frac{1}{2}\cdot\frac{7}{100}=\frac{17}{200} \end{eqnarray}となります。

よって、1番目の人が箱Aから引いて当たってた確率は\[ \frac{\frac{1}{2}\cdot\frac{10}{100} }{\frac{17}{200} }=\frac{10}{17} \]で、箱Bから引いて当たっていた確率は、 $\dfrac{7}{17}$ です。

こうして考えてみると、当たりは全部で17本あり、1番目の人がひいたものが、箱Aにあった10本のどれかなのか、箱Bにあった7本のどれかなのか、と考えると、この条件付き確率は当然の結果のように感じられますね。

この結果から、同じ箱を選んで2番目の人が当たる確率は、
\begin{eqnarray} & & \frac{10}{17}\times\frac{9}{99}+\frac{7}{17}\times\frac{6}{99} \\[5pt] &=& \frac{10 \times 9 +7\times 6}{17\times 99} \\[5pt] &=& \frac{132}{17\times 99} \\[5pt] &=& \frac{4}{51} \\[5pt] \end{eqnarray}となることがわかります。

一方、異なる箱の場合は、（答えが問題文中に書いてありますが）
\begin{eqnarray} & & \frac{10}{17}\times\frac{7}{100}+\frac{7}{17}\times\frac{10}{100} \\[5pt] &=& \frac{10 \times 7 +7\times 10}{17\times 100} \\[5pt] &=& \frac{140}{17\times 100} \\[5pt] &=& \frac{7}{85} \\[5pt] \end{eqnarray}となることがわかります。

両者を比較すると $\dfrac{4}{51}=\dfrac{20}{255}$, $\dfrac{7}{85}=\dfrac{21}{255}$ となり、後者、つまり、異なる箱を選んだほうが、当たる確率が高いことがわかります。

解答

タチツ：451

解答編つづき

問題

今度は異なる箱から引く方が当たりくじを引く確率が大きくなったね。

最初に当たりくじを引いた箱の方が箱 A である確率が大きいのに不思議だね。計算してみないと直観ではわからなかったな。

二つの箱に入っている当たりくじの本数の差が小さくなれば、最初に当たりくじを引いた箱が A である確率と B である確率の差も小さくなるよ。最初に当たりくじを引いた箱がB である場合は、もともと当たりくじが少ない上に前の人がl 本引いてしまっているから当たりくじはなおさら引きにくいね。

なるほどね。箱 A に入っている当たりくじの本数は 10 本として、箱 B に入っている当たりくじが何本であれば同じ箱から引く方がよいのかを調べてみよう。

(3) 箱 A に当たりくじが 10 本入っている場合、1 番目の人が当たりくじを引いたとき、2番目の人が当たりくじを引く確率を大きくするためには、1番目の人が引いた箱と同じ箱、異なる箱のどちらを選ぶべきか。箱 B に入っている当たりくじの本数が 4 本、5 本、6 本、7 本のそれぞれの場合において選ぶべき箱の組み合わせとして正しいものを、次の 0～4 のうちから一つ選べ。 $\myBox{テ}$

解説

今までの内容をまとめると、(1)では、箱Bの当たりが5本のときを考え、この場合は、同じ箱を選んだほうが2番目の人が当たりを引く確率は大きくなるのでした。(2)では、7本のときを考え、この場合は異なる箱を選んだほうがいいのでした。ということで、選択肢から1と2だけが残ります。

6本の場合がどうなるかを考えましょう。

(2)で考えたことを利用すると、1人目の人が当たりを引いたとき、箱Aから引いていた確率は $\dfrac{10}{10+6}=\dfrac{5}{8}$ であり、箱Bだった確率は $\dfrac{3}{8}$ となることがわかります。

1番目に引いて当たった箱と同じ箱を選んだ場合、2番目の人が当たる確率は
\begin{eqnarray} & & \frac{5}{8}\times\frac{9}{99}+\frac{3}{8} \times\frac{5}{99} \\[5pt] &=& \frac{5\times 9+3\times 5}{8\times 99} \\[5pt] &=& \frac{60}{8\times 99} \\[5pt] \end{eqnarray}となります。一方、異なる箱を選んだ場合は \begin{eqnarray} & & \frac{5}{8}\times\frac{6}{100}+\frac{3}{8} \times\frac{10}{100} \\[5pt] &=& \frac{5\times 6+3\times 10}{8\times 100} \\[5pt] &=& \frac{60}{8\times 100} \\[5pt] \end{eqnarray}となります。前者と後者で、分子が同じで、分母は前者の方が小さいので、確率は前者の方が高くなります。つまり、同じ箱を選んだほうがいいことがわかります。

よって、5本、6本のときは同じ箱、7本のときは異なる箱、となっている選択肢1が正解です。