共通テスト 数学I・数学A 2018年度プレテスト 第2問 [1] 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
$\angle \mathrm{ ACB }=90^{\circ}$ である直角三角形 ABC と、その辺上を移動する3点 P, Q, R がある。点 P, Q, R は、次の規則に従って移動する。
- 最初、点 P, Q, R はそれぞれ点 A, B, C の位置にあり、点 P, Q, R は同時刻に移動を開始する。
- 点 P は辺 AC 上を、点 Q は辺 BA 上を、点 R は辺 CB 上を、それぞれ向きを変えることなく、一定の速さで移動する。ただし、点 P は 毎秒 1 の速さで移動する。
- 点 P, Q, R は、それぞれ点 C, A, B の位置に同時刻に到達し、移動を終了する。
次の問いに答えよ。
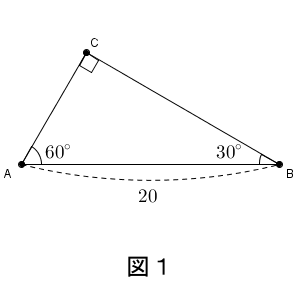
(1) 図1 の直角三角形 ABC を考える。
(i) 各点が移動を開始してから 2 秒後の線分 PQ の長さと三角形 APQ の面積 $S$ を求めよ。
$\mathrm{ PQ }=\myBox{ア}\sqrt{\myBox{イウ} }$
$S=\myBox{エ}\sqrt{\myBox{オ} }$(ii) 各点が移動する間の線分 PR の長さとして、とり得ない値、一回だけとり得る値、二回だけとり得る値を、次の 0~4 のうちからそれぞれすべて選べ。ただし、移動には出発点と到達点も含まれるものとする。
とり得ない値 $\myBox{カ}$
一回だけとり得る値 $\myBox{キ}$
二回だけとり得る値 $\myBox{ク}$0: $5\sqrt{2}$
1: $5\sqrt{3}$
2: $4\sqrt{5}$
3: $10$
4: $10\sqrt{3}$(iii) 各点が移動する間における三角形 APQ, 三角形 BQR, 三角形 CRP の面積をそれぞれ $S_1,S_2,S_3$ とする。各時刻における $S_1,S_2,S_3$ の間の大小関係と、その大小関係が時刻とともにどのように変化するかを答えよ。解答は、解答欄 $\myBox{(う)}$ に記述せよ。
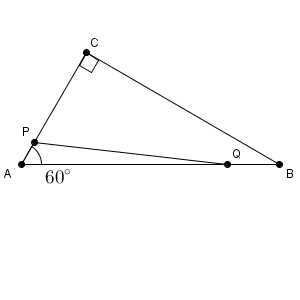
(2) 直角三角形 ABC の辺の長さを右の図2のように変えたとき、三角形 PQR の面積が 12 となるのは、各点が移動を開始してから何秒後かを求めよ。
$\dfrac{\myBox{ケコ}\pm\myBox{サ}\sqrt{\myBox{シ} }}{\myBox{ス} }$ 秒後
考え方
二次関数・三角比が絡んだ問題です。
まずは、正しく状況を把握しましょう。動くものがたくさんありますが、とりあえず、移動開始からの時刻を $x$ とするなどして、いろいろな線分の長さを考えるところから始めましょう。
(1)(i)は、余弦定理を使って求められます。辺の比がわかるので、三平方の定理から求めることもできます。
(1)(ii)は、流れが変わって二次関数の問題です。 $\mathrm{ PR }^2$ の取りうる範囲を考えましょう。
(1)(iii)は、計算により考えることもできますが、図形的に考えることもできます。答えるときは、指示通り、時刻とからめて答えるようにしましょう。
(2)は、(1)(iii)の結果も踏まえて考える問題です。ただ、(1)(iii)を図形的に考えられないと、どう応用できるのかがわかりにくいかもしれません。
話題があちこち飛ぶので、ついていくのが大変です。出てくる図形は易しいですが、問題の難易度は高めです。
【必答問題】
解答編
問題
$\angle \mathrm{ ACB }=90^{\circ}$ である直角三角形 ABC と、その辺上を移動する3点 P, Q, R がある。点 P, Q, R は、次の規則に従って移動する。
- 最初、点 P, Q, R はそれぞれ点 A, B, C の位置にあり、点 P, Q, R は同時刻に移動を開始する。
- 点 P は辺 AC 上を、点 Q は辺 BA 上を、点 R は辺 CB 上を、それぞれ向きを変えることなく、一定の速さで移動する。ただし、点 P は 毎秒 1 の速さで移動する。
- 点 P, Q, R は、それぞれ点 C, A, B の位置に同時刻に到達し、移動を終了する。
次の問いに答えよ。
(1) 図1 の直角三角形 ABC を考える。
解説
まずは状況を整理しましょう。
$\mathrm{ AB }=20$, $\mathrm{ BC }=10\sqrt{3}$, $\mathrm{ CA }=10$ ですね。点 P の動く速さは毎秒 1 なので、 $x$ 秒後なら $\mathrm{ AP }=x$ となります。 $\mathrm{ CA }=10$ なので、 $0\leqq x\leqq 10$ となります。
また、 P, Q, R は同時に目的地に着くのだから、 $\mathrm{ BQ }=2x$ となります。AB は AC の2倍だから、 Q は P の2倍の速さじゃないと、同じタイミングでゴールできません。
同様に考えて、 $\mathrm{ CR }=\sqrt{3}x$ となります。
以上を踏まえて、考えていきます。
解答編 つづき
問題
(i) 各点が移動を開始してから 2 秒後の線分 PQ の長さと三角形 APQ の面積 $S$ を求めよ。
$\mathrm{ PQ }=\myBox{ア}\sqrt{\myBox{イウ} }$
$S=\myBox{エ}\sqrt{\myBox{オ} }$
解説
2秒後時点では、 $\mathrm{ AP }=2$, $\mathrm{ BQ }=4$ となっています。
三角形 APQ で余弦定理を使うと
\begin{eqnarray}
\mathrm{ PQ }^2
&=&
\mathrm{ AP }^2+\mathrm{ AQ }^2-2\mathrm{ AP }\cdot\mathrm{ AQ }\cdot\cos \angle \mathrm{ PAQ } \\[5pt]
&=&
2^2+16^2-2\cdot 2\cdot 16\cdot\frac{1}{2} \\[5pt]
&=&
4+256-32 \\[5pt]
&=&
228 \\[5pt]
\end{eqnarray}となるので、 $\mathrm{ PQ }=\sqrt{228}=2\sqrt{57}$ となります。
また、面積は、
\begin{eqnarray}
& &
\frac{1}{2}\mathrm{ AP }\cdot \mathrm{ AQ }\sin\angle \mathrm{ PAQ } \\[5pt]
&=&
\frac{1}{2}\cdot 2\cdot 16 \cdot \frac{\sqrt{3} }{2} \\[5pt]
&=&
8\sqrt{3}
\end{eqnarray}となります。
解答
アイウ:257
エオ:83
解答編 つづき
問題
(ii) 各点が移動する間の線分 PR の長さとして、とり得ない値、一回だけとり得る値、二回だけとり得る値を、次の 0~4 のうちからそれぞれすべて選べ。ただし、移動には出発点と到達点も含まれるものとする。
とり得ない値 $\myBox{カ}$
一回だけとり得る値 $\myBox{キ}$
二回だけとり得る値 $\myBox{ク}$0: $5\sqrt{2}$
1: $5\sqrt{3}$
2: $4\sqrt{5}$
3: $10$
4: $10\sqrt{3}$
解説
PR の長さは、三角形 CPR で三平方の定理を用いて考えるのがよさそうです。 PR ではなく、 $\mathrm{ PR }^2$ の取りうる値をまずは考えましょう。

$\mathrm{ AP }=x$ なので、 $\mathrm{ CP }=10-x$ です。 $\mathrm{ CR }=\sqrt{3}x$ だったので、
\begin{eqnarray}
\mathrm{ PR }^2
&=&
(10-x)^2+(\sqrt{3}x)^2 \\[5pt]
&=&
x^2-20x+100+3x^2 \\[5pt]
&=&
4x^2-20x+100 \\[5pt]
&=&
4\left(x-\frac{5}{2}\right)^2+75 \\[5pt]
\end{eqnarray}となります。ここで、 $0\leqq x\leqq 10$ の範囲で、 $y=4x^2-20x+100$ のグラフをかいて、 $\mathrm{ PR }^2$ が取りうる値を考えてみましょう。問題文に「出発点と到達点も含む」とあるので、 $x=0$, $x=10$ も含むことに注意しましょう。
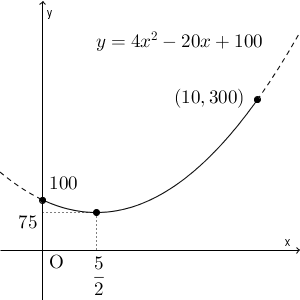
グラフは上のようになります。これを踏まえ、選択肢の値もそれぞれ2乗して、何回値を取りうるかを考えてみましょう。
選択肢0は、2乗すると $(5\sqrt{2})^2=50$ となり、頂点より下だからこの値をとることはありません。
選択肢1は、2乗すると $(5\sqrt{3})^2=75$ となり、頂点の y 座標と一致します。 $\dfrac{5}{2}$ 秒後に一回だけこの値をとることがわかります。
選択肢2は、2乗すると $(4\sqrt{5})^2=80$ となり、この値をとるのは2か所であることがわかります。よって、二回この値をとることがわかります。
選択肢3は、2乗すると $10^2=100$ となり、この値をとるのは2か所であることがわかります。出発点も含むことに注意しましょう。よって、二回この値をとることがわかります。
選択肢4は、2乗すると $(10\sqrt{3})^2=300$ となり、この値をとるのは1か所であることがわかります。到達点も含むことに注意しましょう。よって、一回この値をとることがわかります。
解答
カ:0
キ:1, 4
ク:2, 3
解答編 つづき
問題
(iii) 各点が移動する間における三角形 APQ, 三角形 BQR, 三角形 CRP の面積をそれぞれ $S_1,S_2,S_3$ とする。各時刻における $S_1,S_2,S_3$ の間の大小関係と、その大小関係が時刻とともにどのように変化するかを答えよ。解答は、解答欄 $\myBox{(う)}$ に記述せよ。
解説

具体的に、式を作って考えてみましょう。まず、 $S_1$ は、
\begin{eqnarray}
S_1
&=&
\dfrac{1}{2}\cdot \mathrm{ AP }\cdot \mathrm{ AQ }\cdot\sin\angle \mathrm{ PAQ } \\[5pt]
&=&
\dfrac{1}{2}\cdot x\cdot (20-2x) \cdot\frac{\sqrt{3} }{2} \\[5pt]
&=&
\frac{\sqrt{3} }{2}x(10-x) \\[5pt]
\end{eqnarray}となります。 $S_2$ は、
\begin{eqnarray}
S_2
&=&
\dfrac{1}{2}\cdot \mathrm{ BQ }\cdot \mathrm{ BR }\cdot\sin\angle \mathrm{ QBR } \\[5pt]
&=&
\dfrac{1}{2}\cdot 2x\cdot (10\sqrt{3}-\sqrt{3}x) \cdot\frac{1}{2} \\[5pt]
&=&
\frac{\sqrt{3} }{2}x(10-x) \\[5pt]
\end{eqnarray}となります。同じになりましたね。続いて、 $S_3$ を計算しましょう。
\begin{eqnarray}
S_3
&=&
\dfrac{1}{2}\cdot \mathrm{ CR }\cdot \mathrm{ CP }\cdot\sin\angle \mathrm{ RCP } \\[5pt]
&=&
\dfrac{1}{2}\cdot \sqrt{3}x\cdot (10-x) \cdot 1 \\[5pt]
&=&
\frac{\sqrt{3} }{2}x(10-x) \\[5pt]
\end{eqnarray}となります。
なんということでしょう。全部同じです。問題文には、「各時刻における大小関係」「大小関係が時刻とともにどう変化するか」の両方を書くことが求められています。なので、「移動を開始してから終了するまで、3つの面積はずっと等しい」ということを書けばいいですね。
答えはそれでいいのですが、そもそもなぜこういうことが成り立つのでしょうか。それは、線分の長さではなく、比率に注目するとすぐにわかります。
P, Q, R は同じ時刻に出発し、それぞれ一定の速度で動き、同じ時刻にゴールに行くのだから、「出発地点からその地点まで」と「その地点から目的地点まで」の比率は、3点とも同じになります。つまり、
\begin{eqnarray}
& &
\mathrm{ AP:PC } \\[5pt]
&=&
\mathrm{ BQ:QA } \\[5pt]
&=&
\mathrm{ CR:RB } \\[5pt]
&=&
x:(10-x)
\end{eqnarray}となります。

これを踏まえると、例えば、三角形 APQ の面積は、三角形ABC の面積を基準に考えると、 $\dfrac{\mathrm{ AQ } }{\mathrm{ AB } }$ 倍してから $\dfrac{\mathrm{ AP } }{\mathrm{ AC } }$ 倍したものとなり、つまり、\[ \frac{10-x}{10}\cdot\frac{x}{10}=\frac{x(10-x)}{100} \]倍したものになることがわかります。他の三角形 BQR も、三角形 CRP も、辺の比率は同じなのだから、三角形 ABC の面積の $\dfrac{x(10-x)}{100}$ になることがわかります。
結局 $S_1=S_2=S_3$ となるのは、三角形の形が特別だからではなく、 P, Q, R の動き方が特別だから( $\mathrm{ AP:PC }$, $\mathrm{ BQ:QA }$, $\mathrm{ CR:RB }$ が等しくなるように動いてるから)成り立つことがわかります。
解答
(う):移動を開始してから終了するまで、 $S_1=S_2=S_3$ が成り立つ。
解答編 つづき
問題
(2) 直角三角形 ABC の辺の長さを右の図2のように変えたとき、三角形 PQR の面積が 12 となるのは、各点が移動を開始してから何秒後かを求めよ。
$\dfrac{\myBox{ケコ}\pm\myBox{サ}\sqrt{\myBox{シ} }}{\myBox{ス} }$ 秒後
解説
三角形 PQR の面積を直接求めることは難しそうです。なので、まわりから攻めたほうがいいでしょう。
三角形 ABC の面積は 30 なので、三角形 PQR の面積が 12 ということは、まわり3つの三角形の面積の合計が 18 ということです。ここまではすぐにわかります。
これ以降は、先ほどの問題の(iii)を使うところがポイントです。(iii) の後半で書いたように、まわりの3つの三角形の面積はつねに同じです。
なので、一番求めやすい三角形 CRP の面積が 6 になるときを求めればよく、 $x$ 秒後に面積が 6 になるとすると
\begin{eqnarray}
\frac{1}{2}\cdot (12-x)\cdot \frac{5}{12}x &=& 6 \\[5pt]
(12-x)\cdot 5x &=& 144 \\[5pt]
5x^2-60x+144 &=& 0 \\[5pt]
\end{eqnarray}を解けばいいことがわかります。解の公式から
\begin{eqnarray}
x &=& \frac{30\pm\sqrt{900-5\cdot 144} }{5} \\[5pt]
&=& \frac{30\pm\sqrt{180} }{5} \\[5pt]
&=& \frac{30\pm6\sqrt{5} }{5} \\[5pt]
\end{eqnarray}と求められます。 $\sqrt{5}$ は $2.2$ くらいなので、2つの解は、どちらも0以上12以下となり、どちらも条件を満たします。よって、どちらも解です。
ただ、(iii)の結果が、他の三角形に対しても成り立つこと(つまり、一般化できること)を、予想ではなく、正しく示せる人は、それほど多くはないかもしれません。地道にまわりの3つの三角形の面積を $x$ を使って表すのも、計算は大変です。最後の問題はハードルが高いですね。
解答
ケコサシス:30655






