共通テスト 数学I・数学A 2018年度プレテスト 第1問 [2] 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
関数 $f(x)=a(x-p)^2+q$ について、 $y=f(x)$ のグラフをコンピュータのグラフ表示ソフトを用いて表示させる。
このソフトでは、 $a,p,q$ の値を入力すると、その値に応じたグラフが表示される。さらに、それぞれの $\bbox[2px, border:1px solid]{\qquad \sf{ } }$ の下にある $\bullet$ を左に動かすと値が減少し、右に動かすと値が増加するようになっており、値の変化に応じて関数のグラフが画面上で変化する仕組みになっている。
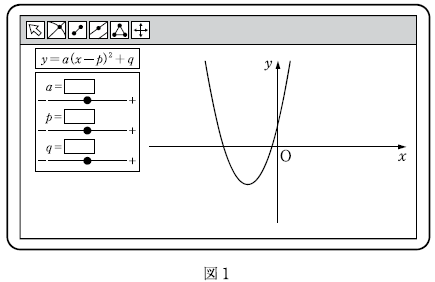
最初に、$a,p,q$ をある値に定めたところ、図1のように、 $x$ 軸の負の部分と2点で交わる下に凸の放物線が表示された。
(1) 図1の放物線を表示させる $a,p,q$ の値に対して、方程式 $f(x)=0$ の解について正しく記述したものを、次の 0~4 のうちから一つ選べ。 $\myBox{ウ}$
0: 方程式 $f(x)=0$ は異なる二つの正の解をもつ。
1: 方程式 $f(x)=0$ は異なる二つの負の解をもつ。
2: 方程式 $f(x)=0$ は正の解と負の解をもつ。
3: 方程式 $f(x)=0$ は重解をもつ。
4: 方程式 $f(x)=0$ は実数解をもたない。(2) 次の操作A、操作P、操作Q のうち、いずれか一つの操作を行い、不等式 $f(x)\gt 0$ の解を考える。
操作A:図1の状態から $p,q$ の値は変えず、 $a$ の値だけを変化させる。
操作P:図1の状態から $a,q$ の値は変えず、 $p$ の値だけを変化させる。
操作Q:図1の状態から $a,p$ の値は変えず、 $q$ の値だけを変化させる。このとき、操作A、操作P、操作Q のうち、「不等式 $f(x)\gt 0$ の解がすべての実数となること」が起こり得る操作は $\myBox{エ}$ 。また、不等式 $f(x)\gt 0$ の解がないこと」が起こり得る操作は $\myBox{オ}$ 。
$\myBox{エ}$, $\myBox{オ}$ に当てはまるものを、次の 0~7 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: ない
1: 操作A だけである
2: 操作P だけである
3: 操作Q だけである4: 操作A と操作P だけである
5: 操作A と操作Q だけである
6: 操作P と操作Q だけである
7: 操作A と操作P と操作Q のすべてである
考え方
去年のプレテストでも出ていた、グラフを動かす問題です。
(1)は、二次関数と二次方程式との関係です。グラフを見れば、選べるでしょう。
(2)は、 $a,p,q$ がグラフのどこに対応しているのか、値を変えるとグラフのどこが動くのかを考えましょう。次に、条件を満たすときにはグラフはどのような状態かを考えましょう。
あまり見慣れない問題かもしれませんが、去年よりはだいぶマイルドな出題になっています。
【必答問題】
解答編
問題
関数 $f(x)=a(x-p)^2+q$ について、 $y=f(x)$ のグラフをコンピュータのグラフ表示ソフトを用いて表示させる。
このソフトでは、 $a,p,q$ の値を入力すると、その値に応じたグラフが表示される。さらに、それぞれの $\bbox[2px, border:1px solid]{\qquad \sf{ } }$ の下にある $\bullet$ を左に動かすと値が減少し、右に動かすと値が増加するようになっており、値の変化に応じて関数のグラフが画面上で変化する仕組みになっている。
最初に、$a,p,q$ をある値に定めたところ、図1のように、 $x$ 軸の負の部分と2点で交わる下に凸の放物線が表示された。
(1) 図1の放物線を表示させる $a,p,q$ の値に対して、方程式 $f(x)=0$ の解について正しく記述したものを、次の 0~4 のうちから一つ選べ。 $\myBox{ウ}$
0: 方程式 $f(x)=0$ は異なる二つの正の解をもつ。
1: 方程式 $f(x)=0$ は異なる二つの負の解をもつ。
2: 方程式 $f(x)=0$ は正の解と負の解をもつ。
3: 方程式 $f(x)=0$ は重解をもつ。
4: 方程式 $f(x)=0$ は実数解をもたない。
解説
$f(x)=0$ の解は、 $y=f(x)$ と $x$ 軸との交点の $x$ 座標と一致します。グラフは、 $x$ 軸の負の部分と2点で交わっているので、異なる二つの負の解を持つことがわかります。なので、1が正解です。
なお、3のように重解を持つのは、グラフが $x$ 軸に接するときです。4のように、実数解を持たないのは、グラフが $x$ 軸と交わっていないときです。
解答
ウ:1
解答編 つづき
問題
(2) 次の操作A、操作P、操作Q のうち、いずれか一つの操作を行い、不等式 $f(x)\gt 0$ の解を考える。
操作A:図1の状態から $p,q$ の値は変えず、 $a$ の値だけを変化させる。
操作P:図1の状態から $a,q$ の値は変えず、 $p$ の値だけを変化させる。
操作Q:図1の状態から $a,p$ の値は変えず、 $q$ の値だけを変化させる。このとき、操作A、操作P、操作Q のうち、「不等式 $f(x)\gt 0$ の解がすべての実数となること」が起こり得る操作は $\myBox{エ}$ 。また、不等式 $f(x)\gt 0$ の解がないこと」が起こり得る操作は $\myBox{オ}$ 。
$\myBox{エ}$, $\myBox{オ}$ に当てはまるものを、次の 0~7 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: ない
1: 操作A だけである
2: 操作P だけである
3: 操作Q だけである4: 操作A と操作P だけである
5: 操作A と操作Q だけである
6: 操作P と操作Q だけである
7: 操作A と操作P と操作Q のすべてである
解説
$a,p,q$ を動かすと $y=a(x-p)^2+q$ の何が動くのかをまずはおさえておきましょう。
$a$ を動かすと、放物線の開き方が変わります。また、符号によっては、上に凸になったり下に凸になったりします。
$p,q$ は、頂点の座標を表しています。 $(p,q)$ が頂点の座標となります。
以上を踏まえて、まずは、「不等式 $f(x)\gt 0$ の解がすべての実数となること」について考えてみましょう。
こうなるとき、グラフ全体が $x$ 軸より上にないといけません。つまり、次の青い太線のグラフのようになっている必要があります。

少なくとも、頂点の $y$ 座標は、正でないといけません。なので、起こりうるとすれば、 $q$ を動かす場合しかありません。
$q$ を大きくして、頂点の $y$ 座標が正になるようにすれば、グラフは下に凸なので、グラフ全体が $x$ 軸より上に来るようになります。こうなれば、「すべての実数」が解になります。
よって、エには、3が入ります。
次に、「不等式 $f(x)\gt 0$ の解がないこと」について考えましょう。
こうなるとき、グラフ全体が $x$ 軸より下にないといけません。頂点を動かしてもダメです。元のグラフは下に凸なので、上に凸に変えないといけません。つまり、 $a$ の値を変える必要があります。
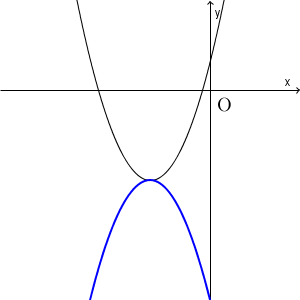
この青い太線のように変えないといけません。 $a$ の値を負にすれば、頂点の $y$ 座標が負であることから、グラフ全体が $x$ 軸より下に来るので、 $f(x)\gt 0$ となる $x$ は存在しないことになります。よって、オには、 $1$ が入ります。
解答
エ:3
オ:1