センター試験 数学I・数学A 2020年度追試 第5問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
$\triangle \mathrm{ PBD }$ の辺 PB 上に2点 P, B のいずれとも異なる点 A をとり、辺 PD 上に2点 P, D のいずれとも異なる点 C をとる。4点 A, B, C, D が同一円周上にあり、 $\mathrm{ AB }=2$, $\mathrm{ PC }=2$, $\mathrm{ PD }=12$ のとき、 $\mathrm{ PA }=\myBox{ア}$ である。
点 M を線分 AB の中点とし、点 N を線分 CD の中点とする。線分 AB を直径とする円と線分 CD を直径とする円が点 E で接していて、3点 M, E, N が一直線上にこの順に並んでいるとする。このとき\[ \mathrm{ MN }=\myBox{イ}\ ,\ \mathrm{ PE }=\myBox{ウ}\sqrt{\myBox{エ} } \]である。また\[ \cos\angle \mathrm{ MPN }=\dfrac{\myBox{オカ} }{\myBox{キク} } \]である。
線分 PN 上に点 F を直線 MF と直線 PN が垂直に交わるようにとり、線分 PM 上に点 G を直線 NG と直線 PM が垂直に交わるようにとる。このとき\[ \mathrm{ PF }=\frac{\myBox{ケコ} }{\myBox{サ} }\ ,\ \mathrm{ PG }=\frac{\myBox{シス} }{\myBox{セ} } \]である。さらに、線分 MF と線分 NG の交点を J とする。このとき\[ \mathrm{ JE }=\frac{\myBox{ソ}\sqrt{\myBox{タ} }}{\myBox{チツ} } \]である。
考え方
図がかきにくい上、PE がどういう直線なのかがわからないと、なかなか進めません。しかも、それが序盤に出てくるのでやっかいです。それさえわかれば、後半は特に難しいところはありません。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
$\triangle \mathrm{ PBD }$ の辺 PB 上に2点 P, B のいずれとも異なる点 A をとり、辺 PD 上に2点 P, D のいずれとも異なる点 C をとる。4点 A, B, C, D が同一円周上にあり、 $\mathrm{ AB }=2$, $\mathrm{ PC }=2$, $\mathrm{ PD }=12$ のとき、 $\mathrm{ PA }=\myBox{ア}$ である。
解説
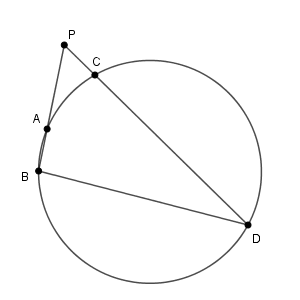
$\mathrm{ PA }=x$ とすると、方べきの定理より
\begin{eqnarray}
\mathrm{ PA }\cdot \mathrm{ PB } &=& \mathrm{ PC }\cdot \mathrm{ PD } \\[5pt]
x\cdot (x+2) &=& 2\cdot 12 \\[5pt]
x^2+2x-24 &=& 0 \\[5pt]
(x-4)(x+6) &=& 0 \\[5pt]
x &=& 4, -6
\end{eqnarray}となります。 $\mathrm{ PA }\gt 0$ なので、 $\mathrm{ PA }=4$ です。
解答
ア:4
解答編 つづき
問題
点 M を線分 AB の中点とし、点 N を線分 CD の中点とする。線分 AB を直径とする円と線分 CD を直径とする円が点 E で接していて、3点 M, E, N が一直線上にこの順に並んでいるとする。このとき\[ \mathrm{ MN }=\myBox{イ}\ ,\ \mathrm{ PE }=\myBox{ウ}\sqrt{\myBox{エ} } \]である。
解説
図は次のようになっています。
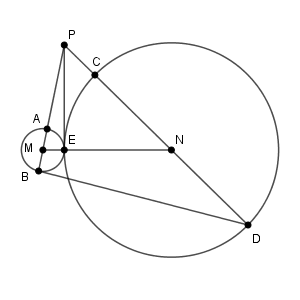
M, E, N がこの順に一直線上に並んでいるので
\begin{eqnarray}
\mathrm{ MN }
&=&
\mathrm{ ME }+\mathrm{ EN } \\[5pt]
&=&
\frac{\mathrm{ AB } }{2}+\frac{\mathrm{ CD } }{2} \\[5pt]
&=&
1+5=6
\end{eqnarray}となります。
次に、線分 PE の長さを考えます。そのために、まず、PE が2つの円とどのように共有点を持っているかを考えます。
直線 PE が2つの円と2点で交わっているとします。わかりやすいように極端にかくと、次のような図です。
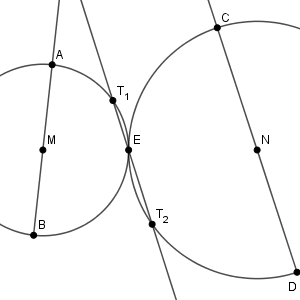
線分 AB を直径する円との共有点のうち、 E と異なるものを $\mathrm{T_1}$ とし、線分 CD を直径する円との共有点のうち、 E と異なるものを $\mathrm{T_2}$ としています。
2つの円は点 E で接するので、片方の円とだけ接することはありません。また、 $\mathrm{T_1,E,T_2}$ と並ぶ(上の図)か、$\mathrm{T_2,E,T_1}$ と並ぶ場合しかありません。
$\mathrm{T_1,E,T_2}$ と並ぶとすると、方べきの定理から
\begin{eqnarray}
\mathrm{ PE }^2\gt\mathrm{ PE }\cdot \mathrm{ PT_1 }=\mathrm{ PA }\cdot \mathrm{ PB }=24
\end{eqnarray}であり、同じく方べきの定理から
\begin{eqnarray}
\mathrm{ PE }^2\lt\mathrm{ PE }\cdot \mathrm{ PT_2 }=\mathrm{ PC }\cdot \mathrm{ PD }=24
\end{eqnarray}となりますが、こんなことは起こり得ません。同様に、 $\mathrm{T_2,E,T_1}$ となることもありません。
つまり、PE は2つの円の接線となります。よって、三平方の定理より
\begin{eqnarray}
\mathrm{ PE }
&=&
\sqrt{\mathrm{ PM }^2-\mathrm{ ME }^2} \\[5pt]
&=&
\sqrt{5^2-1^2} \\[5pt]
&=&
2\sqrt{6}
\end{eqnarray}となります。
PE は次のようにして求めることもできます。余弦定理より
\begin{eqnarray}
\cos\angle \mathrm{ PEM }
&=&
\frac{\mathrm{ PE }^2+\mathrm{ EM }^2-\mathrm{ PM }^2}{2\cdot \mathrm{ PE }\cdot \mathrm{ EM } } \\[5pt]
&=&
\frac{\mathrm{ PE }^2+1^2-5^2}{2\cdot \mathrm{ PE }\cdot 1} \\[5pt]
&=&
\frac{\mathrm{ PE }^2-24}{2\mathrm{ PE } } \\[5pt]
\end{eqnarray}であり、
\begin{eqnarray}
\cos\angle \mathrm{ PEN }
&=&
\frac{\mathrm{ PE }^2+\mathrm{ EN }^2-\mathrm{ PN }^2}{2\cdot \mathrm{ PE }\cdot \mathrm{ EN } } \\[5pt]
&=&
\frac{\mathrm{ PE }^2+5^2-7^2}{2\cdot \mathrm{ PE }\cdot 5} \\[5pt]
&=&
\frac{\mathrm{ PE }^2-24}{10\mathrm{ PE } } \\[5pt]
\end{eqnarray}となります。 $\angle \mathrm{ PEM }+\angle \mathrm{ PEN }=180^{\circ}$ だから $\cos\angle \mathrm{ PEM }=-\cos\angle\mathrm{PEN}$ なので
\begin{eqnarray}
\frac{\mathrm{ PE }^2-24}{2\mathrm{ PE } } &=& -\frac{\mathrm{ PE }^2-24}{10\mathrm{ PE } } \\[5pt]
5(\mathrm{ PE }^2-24) &=& -(\mathrm{ PE }^2-24) \\[5pt]
\mathrm{ PE }^2 &=& 24 \\[5pt]
\mathrm{ PE } &=& 2\sqrt{6} \\[5pt]
\end{eqnarray}となります。
解答
イ:6
ウエ:26
解答編 つづき
問題
また\[ \cos\angle \mathrm{ MPN }=\dfrac{\myBox{オカ} }{\myBox{キク} } \]である。
解説
これは余弦定理を使うしかなさそうです。
\begin{eqnarray}
\cos\angle \mathrm{ MPN }
&=&
\frac{\mathrm{ MP }^2+\mathrm{ PN }^2-\mathrm{ MN }^2 }{2\mathrm{ MP }\cdot \mathrm{ PN } } \\[5pt]
&=&
\frac{5^2+7^2-6^2}{2\cdot5\cdot 7} \\[5pt]
&=&
\frac{19}{35} \\[5pt]
\end{eqnarray}となります。
解答
オカキク:1935
解答編 つづき
問題
線分 PN 上に点 F を直線 MF と直線 PN が垂直に交わるようにとり、線分 PM 上に点 G を直線 NG と直線 PM が垂直に交わるようにとる。このとき\[ \mathrm{ PF }=\frac{\myBox{ケコ} }{\myBox{サ} }\ ,\ \mathrm{ PG }=\frac{\myBox{シス} }{\myBox{セ} } \]である。
解説
図は次のようになっています。
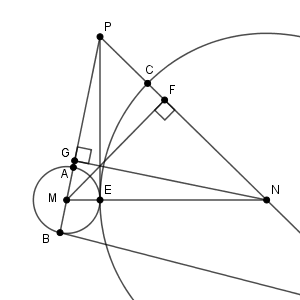
余弦の値がわかっているので
\begin{eqnarray}
\mathrm{ PF }
&=&
\mathrm{ PM }\cos\angle \mathrm{ MPN } \\[5pt]
&=&
5\cdot\frac{19}{35} \\[5pt]
&=&
\frac{19}{7} \\[5pt]
\end{eqnarray}であり、
\begin{eqnarray}
\mathrm{ PG }
&=&
\mathrm{ PN }\cos\angle \mathrm{ MPN } \\[5pt]
&=&
7\cdot\frac{19}{35} \\[5pt]
&=&
\frac{19}{5} \\[5pt]
\end{eqnarray}となります。
解答
ケコサ:197
シスセ:195
解答編 つづき
問題
さらに、線分 MF と線分 NG の交点を J とする。このとき\[ \mathrm{ JE }=\frac{\myBox{ソ}\sqrt{\myBox{タ} }}{\myBox{チツ} } \]である。
解説
図は次のようになっています。
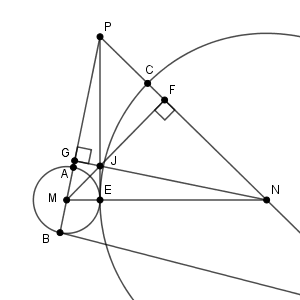
J は、三角形 PMN の垂心です。また、 PE と MN は垂直だから、 J は PE 上の点です。なので、\[ \mathrm{ JE }=\mathrm{ PE }-\mathrm{ PJ } \]が成り立ちます。
三角形 PGJ と三角形 PEM は相似だから
\begin{eqnarray}
\mathrm{ JE }
&=&
\mathrm{ PE }-\mathrm{ PJ } \\[5pt]
&=&
2\sqrt{6}-\frac{\mathrm{ PM }\cdot\mathrm{ PG } }{\mathrm{ PE } } \\[5pt]
&=&
2\sqrt{6}-\frac{5\cdot\frac{19}{5} }{2\sqrt{6} } \\[5pt]
&=&
2\sqrt{6}-\frac{19\sqrt{6} }{12} \\[5pt]
&=&
\frac{5\sqrt{6} }{12} \\[5pt]
\end{eqnarray}となります。
解答
ソタチツ:5612





