センター試験 数学I・数学A 2020年度追試 第2問 [1] 解説
【必答問題】
問題編
問題
$\triangle \mathrm{ ABP }$ において、 $\mathrm{ AP }=6$, $\mathrm{ BP }=2\sqrt{17}$, $\sin\angle \mathrm{ PAB }=\dfrac{2\sqrt{2} }{3}$, $\mathrm{ AB }\lt \mathrm{ AP }$ とする。
次の $\mybox{イ}$ に当てはまるものを、下の 0 ~ 2 のうちから一つ選べ。
$\mathrm{ AB }=\myBox{ア}$ であり、 $\angle \mathrm{ PAB }$ は $\myBox{イ}$ である。
0: 鋭角
1: 直角
2: 鈍角直線 AB 上に点 C を、3点 A, B, C がこの順に並び、かつ $\mathrm{ CP }=3\sqrt{17}$ となるようにとる。このとき\[ \mathrm{ AC }=\myBox{ウ}\ , \ \mathrm{ BC }=\myBox{エ} \]である。したがって、 $\triangle \mathrm{ PBC }$ の外接円の半径 $R$ は\[ R=\frac{\myBox{オカ}\sqrt{\myBox{キ} }}{\myBox{ク} } \]である。この外接円の中心を O とすると\[ \mathrm{ AO }^2-R^2=\myBox{ケコ} \]である。
考え方
最初からなかなか取り組みにくいです。場合分けなどが必要で、少し手間取りそうです。
最初さえクリアできれば、後はよくあるながれが続きますが、最後はまた少し考えないといけません。 $\mathrm{ AO }^2$ を直接求めるのは難しそうなので、図形をよく見て工夫して求めるようにしましょう。
【必答問題】
解答編
問題
$\triangle \mathrm{ ABP }$ において、 $\mathrm{ AP }=6$, $\mathrm{ BP }=2\sqrt{17}$, $\sin\angle \mathrm{ PAB }=\dfrac{2\sqrt{2} }{3}$, $\mathrm{ AB }\lt \mathrm{ AP }$ とする。
次の $\mybox{イ}$ に当てはまるものを、下の 0 ~ 2 のうちから一つ選べ。
$\mathrm{ AB }=\myBox{ア}$ であり、 $\angle \mathrm{ PAB }$ は $\myBox{イ}$ である。
0: 鋭角
1: 直角
2: 鈍角
解説
$\mathrm{AB}$ を求めるために正弦定理や余弦定理を使いたいところですが、角に関する情報は $\sin\angle \mathrm{ PAB }$ しかわかっていません。
$\cos\angle \mathrm{ PAB }$ の値がわかれば余弦定理が使えます。ただ、わかるのは\[ \cos^2\angle \mathrm{ PAB }=1-\dfrac{8}{9}=\dfrac{1}{9} \]までで、今の段階では正の値か負の値かはわかりません。なので、場合分けをして考えていきます。
$\cos\angle \mathrm{ PAB }=\dfrac{1}{3}$ とします。 $\mathrm{ AB }=x$ として、余弦定理から
\begin{eqnarray}
\mathrm{ BP }^2 &=& \mathrm{ AB }^2+\mathrm{ AP }^2-2\mathrm{ AB }\cdot \mathrm{ AP }\cos\angle \mathrm{ PAB } \\[5pt]
68 &=& x^2+36-2x\cdot 6\cdot \frac{1}{3} \\[5pt]
0 &=& x^2-32-4x \\[5pt]
\end{eqnarray}となります。二次方程式を解いて
\begin{eqnarray}
(x+4)(x-8) &=& 0 \\[5pt]
x &=& -4,8
\end{eqnarray}と求められます。しかし、 $\mathrm{ AB }\lt \mathrm{ AP }$ を満たすものがないので、この場合、解はありません。
次に、 $\cos\angle \mathrm{ PAB }=-\dfrac{1}{3}$ とします。余弦定理から
\begin{eqnarray}
\mathrm{ BP }^2 &=& \mathrm{ AB }^2+\mathrm{ AP }^2-2\mathrm{ AB }\cdot \mathrm{ AP }\cos\angle \mathrm{ PAB } \\[5pt]
68 &=& x^2+36-2x\cdot 6\cdot \left(-\frac{1}{3}\right) \\[5pt]
0 &=& x^2-32+4x \\[5pt]
\end{eqnarray}となります。二次方程式を解いて
\begin{eqnarray}
(x-4)(x+8) &=& 0 \\[5pt]
x &=& 4,-8
\end{eqnarray}となります。 $\mathrm{ AB }\lt \mathrm{ AP }$ を満たすものは $x=4$ だけです。
以上から、 $\mathrm{ AB }=4$ です。また、 $\cos\angle \mathrm{ PAB }=-\dfrac{1}{3}$ で、負なので、 $\angle \mathrm{ PAB }$ は鈍角です。
解答
ア:4
イ:2
解答編 つづき
問題
直線 AB 上に点 C を、3点 A, B, C がこの順に並び、かつ $\mathrm{ CP }=3\sqrt{17}$ となるようにとる。このとき\[ \mathrm{ AC }=\myBox{ウ}\ , \ \mathrm{ BC }=\myBox{エ} \]である。
解説
$\cos\angle \mathrm{ PAC }=\cos\angle \mathrm{ PAB }=-\dfrac{1}{3}$ です。
三角形 ACP で考えます。 $\mathrm{ AC }=x$ とすると、余弦定理から
\begin{eqnarray}
\mathrm{ CP }^2 &=& \mathrm{ AC }^2+\mathrm{ AP }^2-2\mathrm{ AC }\cdot \mathrm{ AP }\cos\angle \mathrm{ CAP } \\[5pt]
(3\sqrt{17})^2 &=& x^2+6^2-2x\cdot 6\cdot \left(-\frac{1}{3}\right) \\[5pt]
153 &=& x^2+36+4x \\[5pt]
\end{eqnarray}がわかります。二次方程式を解いて
\begin{eqnarray}
x^2+4x-117 &=& 0 \\[5pt]
(x-9)(x+13) &=& 0 \\[5pt]
x &=& 9,-13
\end{eqnarray}となり、 $x\gt 0$ なので、 $\mathrm{ AC }=9$ となることがわかります。また、\[ \mathrm{ BC }=\mathrm{ AC }-\mathrm{ AB }=9-4=5 \]です。
解答
ウ:9
エ:5
解答編 つづき
問題
したがって、 $\triangle \mathrm{ PBC }$ の外接円の半径 $R$ は\[ R=\frac{\myBox{オカ}\sqrt{\myBox{キ} }}{\myBox{ク} } \]である。
解説
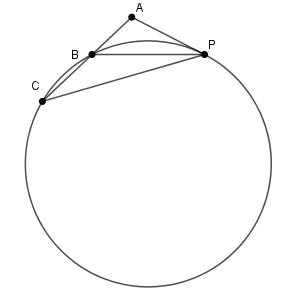
外接円の半径を求めるには、どれかの角の正弦の値がわかればいいです。今、三角形 PBC の3辺の長さがわかっているので、余弦定理を使い、相互関係から正弦の値を求め、正弦定理を使って外接円の半径を求めることができます。(問題文では、 BC の長さを求めた後に、「したがって」と続くので、この解法が想定されていると思います)
しかし、この方法は少し計算がめんどうなので、ここでは、別の方法を使って解いてみます。三角形 ACP で考えると、正弦定理から
\begin{eqnarray}
\dfrac{\mathrm{ CP } }{\sin\angle \mathrm{ CAP } } &=& \frac{\mathrm{ AP } }{\sin\angle \mathrm{ ACP } } \\[5pt]
\dfrac{3\sqrt{17} }{\frac{2\sqrt{2} }{3} } &=& \frac{6}{\sin\angle \mathrm{ ACP } } \\[5pt]
\sin\angle \mathrm{ ACP } &=& 6\cdot \dfrac{\frac{2\sqrt{2} }{3} }{3\sqrt{17} } \\[5pt]
&=& \dfrac{4\sqrt{2} }{3\sqrt{17} } \\[5pt]
\end{eqnarray}となります。
次に、三角形 PBC で正弦定理を使うと
\begin{eqnarray}
2R
&=&
\frac{\mathrm{ BP } }{\sin\angle \mathrm{ BCP } } \\[5pt]
&=&
2\sqrt{17} \cdot \dfrac{3\sqrt{17} }{4\sqrt{2} } \\[5pt]
&=&
\dfrac{51}{2\sqrt{2} } \\[5pt]
\end{eqnarray}なので、\[ R=\frac{51\sqrt{2} }{8} \]と求められます。
解答
オカキク:5128
解答編 つづき
問題
この外接円の中心を O とすると\[ \mathrm{ AO }^2-R^2=\myBox{ケコ} \]である。
解説
$\mathrm{ AO }^2$ の長さを直接求めるのは難しそうなので、工夫して求めることを考えます。
2つの方法で解いてみます。
BC の中点を M とします。このとき、 AC と OM は垂直になります。
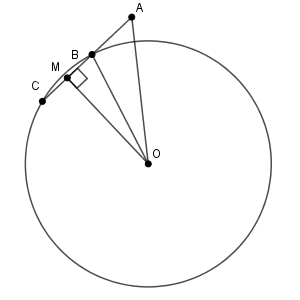
三角形 AMO は直角三角形だから\[ \mathrm{ AO }^2=\mathrm{ AM }^2+\mathrm{ MO }^2 \]が成り立ちます。また、三角形 BMO も直角三角形なので、\[ R^2=\mathrm{ BO }^2=\mathrm{ BM }^2+\mathrm{ MO }^2 \]が成り立ちます。
よって、
\begin{eqnarray}
\mathrm{ AO }^2-R^2
&=&
\mathrm{ AM }^2-\mathrm{ BO }^2 \\[5pt]
&=&
\left(4+\frac{5}{2}\right)^2-\left(\frac{5}{2}\right)^2 \\[5pt]
&=&
36
\end{eqnarray}と求められます。
別の方法でも求めてみます。点 A から外接円に接線を引き、接点を T とします。
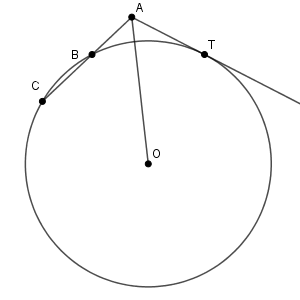
$\mathrm{ AO }^2-R^2$ とは、 $\mathrm{ AT }^2$ のことです。ここで、方べきの定理より\[ \mathrm{ AT }^2=\mathrm{ AB }\cdot \mathrm{ AC }=4\cdot 9=36 \]と求めることもできます。三角比の問題なのでこれが想定解法ではないかもしれませんが、方べきの定理を使った方が簡単です。
解答
ケコ:36





