センター試験 数学I・数学A 2020年度追試 第2問 [2] 解説

問題文中の画像は、大学入試センターのサイトから取得しています。

【必答問題】

問題編

問題

　高等学校（中等教育学校を含む）の卒業者のうち、大学または短期大学に進学した者の割合（以下、進学率）と、就職した者の割合（以下、就職率）が47都道府県別に公表されている。

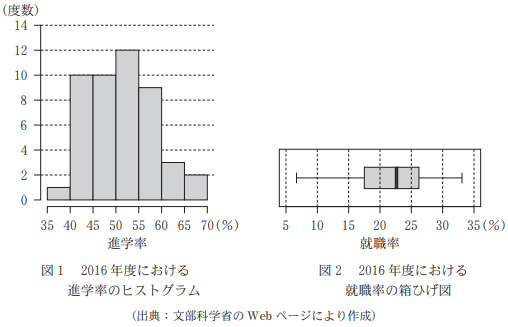
(1) 図１は2016年度における都道府県別の進学率のヒストグラムであり、図２は2016年度における都道府県別の就職率の箱ひげ図である。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　次の $\mybox{サ}$ に当てはまるものを、下の 0 ～ 3 のうちから一つ選べ。

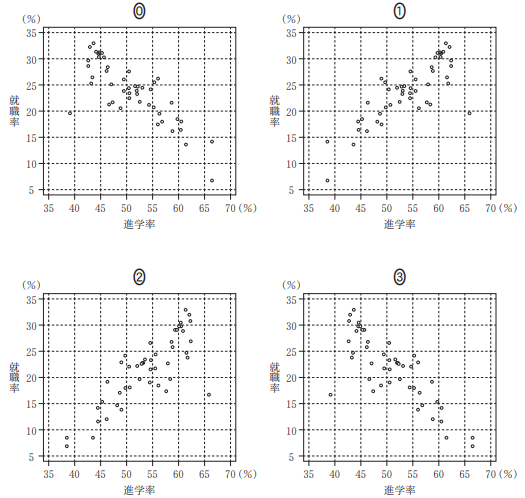
　2016年度における都道府県別の進学率（横軸）と就職率（縦軸）の散布図は $\myBox{サ}$ である。

---

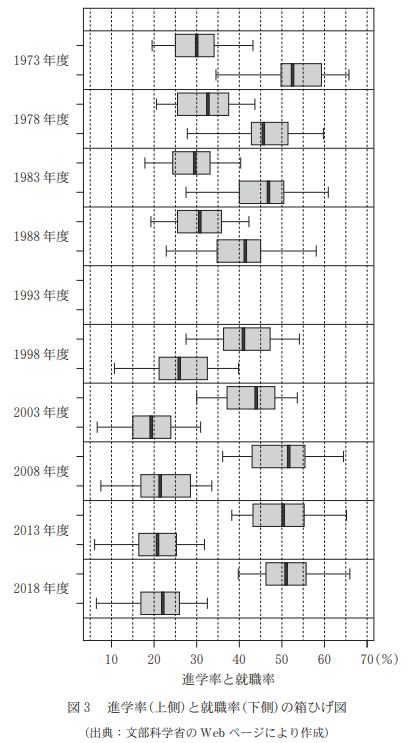
(2) 図３は、1973年度から2018年度まで、5年ごとの10個の年度（それぞれを時点という）における都道府県別の進学率（上側）と就職率（下側）を箱ひげ図で表したものである。ただし、設問の都合で1993年度における箱ひげ図は表示していない。
　次の $\mybox{シ}$ に当てはまるものを、下の 0 ～ 4 のうちから一つ選べ。

　図３から読み取れることとして、正しい記述は $\myBox{シ}$ である。

　0: 1993年度を除く9時点すべてにおいて、進学率の左側のひげの長さと右側のひげの長さを比較すると、右側のほうが長い。

　1: 2003年度、2008年度、2013年度、2018年度の４時点すべてにおいて、就職率の左側のひげの長さと右側のひげの長さを比較すると、左側のほうが長い。

　2: 2003年度、2008年度、2013年度、2018年度の４時点すべてにおいて、就職率の四分位範囲は、それぞれの直前の時点より減少している。

　3: 1993年度を除く時点ごとに進学率と就職率の四分位範囲を比較すると、つねに就職率の方が大きい。

　4: 就職率について、1993年度を除くどの時点においても最大値は最小値の2倍以上である。

---

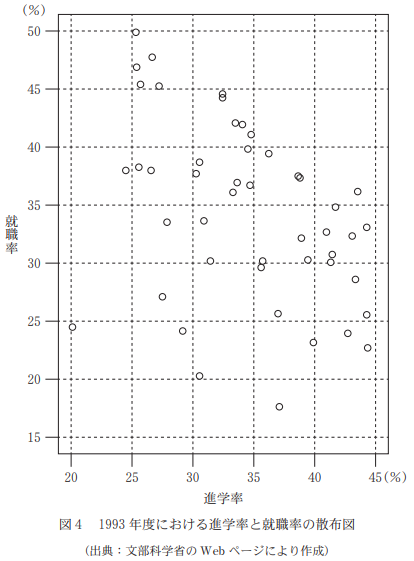
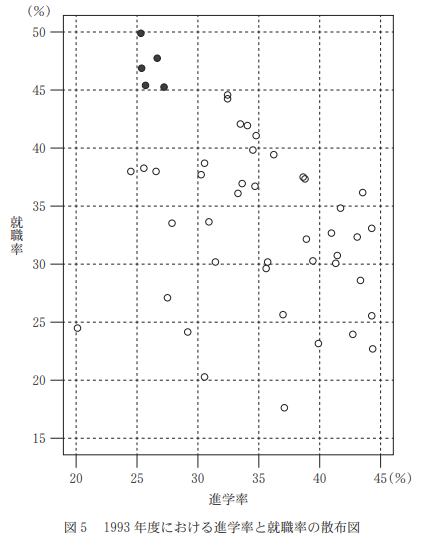
(3) 図４は、1993年度における都道府県別の進学率（横軸）と就職率（縦軸）の散布図である。

　次の $\mybox{ス}$, $\mybox{セ}$ に当てはまる最も適切なものを、それぞれの解答群から一つずつ選べ。

　1993年度における就職率の $\myBox{ス}$ は 34.8% である。
　また、1993年度における進学率の $\mybox{ス}$ は $\myBox{セ}$ %である。

$\myBox{ス}$ の解答群
　0: 最小値
　1: 中央値
　2: 最大値
　3: 第1四分位数
　4: 第3四分位数
　5: 四分位範囲

$\myBox{セ}$ の解答群
　0: $10.0$
　1: $20.1$
　2: $29.7$
　3: $34.5$
　4: $39.7$
　5: $44.4$

---

(4) 図４に記した1993年度における都道府県別の進学率と就職率の相関係数を計算したところ、 $-0.41$ であった。就職率が 45% を超えている5都道府県を黒丸で示したのが図５である。
　次の $\mybox{ソ}$ に当てはまるものを、下の 0 ～ 5 のうちから一つ選べ。

　就職率が 45% を超えている5都道府県を除外したときの相関係数を $r$ とおくと、 $\myBox{ソ}$ である。

　0: $r\lt -0.41$
　1: $r=-0.41$
　2: $-0.41 \lt r \lt 0$
　3: $r=0$
　4: $0\lt r\lt 0.41$
　5: $r\geqq 0.41$

---

(5) 1993年度における進学率 $X$, 就職率 $Y$ について、 $X$ の平均値の2乗の値を求めたい。 $X^2$ の平均値、 $Y$ の平均値と標準偏差、 $X$ と $Y$ の共分散と相関係数は表１のとおりであった。ただし、 $X$ と $Y$ の共分散とは、 $X$ の偏差と $Y$ の偏差の積の平均値である。なお、表１の数値は正確な値であり、四捨五入されていないものとする。

表１ 2乗の平均値、平均値、標準偏差、共分散、および相関係数

$X^2$ の 平均値	$1223$
$Y$ の 平均値	$34$
$Y$ の 標準偏差	$7.6$
$X$ と $Y$ の 共分散	$-20$
$X$ と $Y$ の 相関係数	$-0.41$

　また、必要であれば以下の事実を用いてもよい。

　$n$ を自然数とする。実数値のデータ $u_1, u_2,\cdots,u_n$ に対して、平均値を $\bar{u}$ 、分散を $s^2$ とおくと\[ s^2=\frac{u_1^2+u_2^2+\cdots+u_n^2}{n} -(\bar{u})^2 \]が成り立つ。

　$X$ の標準偏差は、小数第2位を四捨五入すると、 $\myBox{タ}.\myBox{チ}$ である。

　次の $\mybox{ツ}$ に当てはまる数値として最も近いものを、下の 0 ～ 7 のうちから一つ選べ。

　$X$ の平均値の2乗の値は $\myBox{ツ}$ である。

　0: $1122$
　1: $1156$
　2: $1182$
　3: $1223$
　4: $1260$
　5: $1296$
　6: $1332$
　7: $1369$

考え方

(1)は、矛盾するものを消去していきましょう。(5)はヒントが書いてあるので、それを使えば難しくはないでしょう。計算は少し面倒ですが。

問題文中の画像は、大学入試センターのサイトから取得しています。

【必答問題】

解答編

問題

　高等学校（中等教育学校を含む）の卒業者のうち、大学または短期大学に進学した者の割合（以下、進学率）と、就職した者の割合（以下、就職率）が47都道府県別に公表されている。

(1) 図１は2016年度における都道府県別の進学率のヒストグラムであり、図２は2016年度における都道府県別の就職率の箱ひげ図である。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　次の $\mybox{サ}$ に当てはまるものを、下の 0 ～ 3 のうちから一つ選べ。

　2016年度における都道府県別の進学率（横軸）と就職率（縦軸）の散布図は $\myBox{サ}$ である。

解説

確実に除外できる選択肢をはずして考えていきます。

進学率のヒストグラムを見ると、各階級の度数がわかるので、これをもとに不適切なものを除外します。35以上45未満の階級の度数は1なので、散布図で、進学率が35以上40未満のところに2点ある選択肢1と選択肢2は適切ではないことがわかります。

また、就職率の箱ひげ図を見ると、第一四分位数は15と20の間です。データは47個あるので、中央値は下から24個目、第一四分位数は下から12個目です。

選択肢0の散布図で、下から点を数えていくと、下から12個目の値は20以上25以下の範囲にあることがわかります。なので、第一四分位数が20より小さくなることはありません。

こうして、選択肢3だけが残ります。

解答

サ：3

解答編 つづき

問題

(2) 図３は、1973年度から2018年度まで、5年ごとの10個の年度（それぞれを時点という）における都道府県別の進学率（上側）と就職率（下側）を箱ひげ図で表したものである。ただし、設問の都合で1993年度における箱ひげ図は表示していない。
　次の $\mybox{シ}$ に当てはまるものを、下の 0 ～ 4 のうちから一つ選べ。

　図３から読み取れることとして、正しい記述は $\myBox{シ}$ である。

　0: 1993年度を除く9時点すべてにおいて、進学率の左側のひげの長さと右側のひげの長さを比較すると、右側のほうが長い。

　1: 2003年度、2008年度、2013年度、2018年度の４時点すべてにおいて、就職率の左側のひげの長さと右側のひげの長さを比較すると、左側のほうが長い。

　2: 2003年度、2008年度、2013年度、2018年度の４時点すべてにおいて、就職率の四分位範囲は、それぞれの直前の時点より減少している。

　3: 1993年度を除く時点ごとに進学率と就職率の四分位範囲を比較すると、つねに就職率の方が大きい。

　4: 就職率について、1993年度を除くどの時点においても最大値は最小値の2倍以上である。

解説

1つ1つ見ていきます。

選択肢0は、進学率なので上側の箱ひげ図を見ます。2003年度を見ると、左側のひげのほうが長いので、間違いです。

選択肢1は、就職率なので下側の箱ひげ図を見ます。2003年度以降は確かに左のひげのほうが長いです。これが正しいです。

選択肢2は、四分位範囲なので、箱の横幅を見ます。2008年度は箱の幅が直前の時点より広がっているので、間違いです。

選択肢3も、箱の横幅を見ます。1978年度を見ると、進学率の四分位範囲のほうが就職率の四分位範囲より大きいので、間違いです。

選択肢4は、1973年度を見ると、就職率の最大値は約65%、最小値は約35%なので、2倍以上ではありません。よって、間違いです。

以上から、選択肢1が正解です。

解答

シ：1

解答編 つづき

問題

(3) 図４は、1993年度における都道府県別の進学率（横軸）と就職率（縦軸）の散布図である。

　次の $\mybox{ス}$, $\mybox{セ}$ に当てはまる最も適切なものを、それぞれの解答群から一つずつ選べ。

　1993年度における就職率の $\myBox{ス}$ は 34.8% である。
　また、1993年度における進学率の $\mybox{ス}$ は $\myBox{セ}$ %である。

$\myBox{ス}$ の解答群
　0: 最小値
　1: 中央値
　2: 最大値
　3: 第1四分位数
　4: 第3四分位数
　5: 四分位範囲

$\myBox{セ}$ の解答群
　0: $10.0$
　1: $20.1$
　2: $29.7$
　3: $34.5$
　4: $39.7$
　5: $44.4$

解説

まず、就職率の何が34.8%なのかを考えます。

縦軸で見ると、最大値が約50、最小値が約17.5です。この時点で、最小値や最大値ではないことがわかり、四分位範囲でもないことがわかります。

中央値は下から24個目、第1四分位数は下から12個目、第3四分位数は上から12個目です。数えて34.8%になる点を見つけると、中央値であることがわかります。

進学率の中央値は、右から24個目を調べればよく、34.5%が最も適切であることがわかります。

解答

ス：1
セ：3

解答編 つづき

問題

(4) 図４に記した1993年度における都道府県別の進学率と就職率の相関係数を計算したところ、 $-0.41$ であった。就職率が 45% を超えている5都道府県を黒丸で示したのが図５である。
　次の $\mybox{ソ}$ に当てはまるものを、下の 0 ～ 5 のうちから一つ選べ。

　就職率が 45% を超えている5都道府県を除外したときの相関係数を $r$ とおくと、 $\myBox{ソ}$ である。

　0: $r\lt -0.41$
　1: $r=-0.41$
　2: $-0.41 \lt r \lt 0$
　3: $r=0$
　4: $0\lt r\lt 0.41$
　5: $r\geqq 0.41$

解説

5つの黒丸は、「就職率が高いと進学率が低い」を表しているもので、相関係数のマイナスに寄与していると考えられます。これら5つの点を除けば、この傾向が弱まります。白い点だけを見ると相関がなさそうに見えることからもわかります。

相関係数は $0$ に近づくと考えられるので、 $-0.41\lt r \lt 0$ が正しいです。

解答

ソ：2

解答編 つづき

問題

(5) 1993年度における進学率 $X$, 就職率 $Y$ について、 $X$ の平均値の2乗の値を求めたい。 $X^2$ の平均値、 $Y$ の平均値と標準偏差、 $X$ と $Y$ の共分散と相関係数は表１のとおりであった。ただし、 $X$ と $Y$ の共分散とは、 $X$ の偏差と $Y$ の偏差の積の平均値である。なお、表１の数値は正確な値であり、四捨五入されていないものとする。

表１ 2乗の平均値、平均値、標準偏差、共分散、および相関係数

$X^2$ の 平均値	$1223$
$Y$ の 平均値	$34$
$Y$ の 標準偏差	$7.6$
$X$ と $Y$ の 共分散	$-20$
$X$ と $Y$ の 相関係数	$-0.41$

　また、必要であれば以下の事実を用いてもよい。

　$n$ を自然数とする。実数値のデータ $u_1, u_2,\cdots,u_n$ に対して、平均値を $\bar{u}$ 、分散を $s^2$ とおくと\[ s^2=\frac{u_1^2+u_2^2+\cdots+u_n^2}{n} -(\bar{u})^2 \]が成り立つ。

　$X$ の標準偏差は、小数第2位を四捨五入すると、 $\myBox{タ}.\myBox{チ}$ である。

　次の $\mybox{ツ}$ に当てはまる数値として最も近いものを、下の 0 ～ 7 のうちから一つ選べ。

　$X$ の平均値の2乗の値は $\myBox{ツ}$ である。

　0: $1122$
　1: $1156$
　2: $1182$
　3: $1223$
　4: $1260$
　5: $1296$
　6: $1332$
　7: $1369$

解説

共分散をそれぞれの標準偏差で割ったものが相関係数です。なので、 $X$ の標準偏差を $x$ とすると
\begin{eqnarray} \frac{-20}{x\cdot 7.6} &=& -0.41 \\[5pt] x &=& \frac{-20}{-0.41\cdot 7.6} \\[5pt] &=& 6.418\cdots \end{eqnarray}となるので、小数第2位を四捨五入すると $6.4$ となります。

これをもとに考えると、 $X$ の分散は $6.4^2$ です。問題文中のヒントから、 $X$ の平均値の2乗の値は、 $x^2$ の平均値から分散を引けば求められるので
\begin{eqnarray} 1223-6.4^2 &=& 1223-40.96 \\[5pt] &=& 1182.04 \end{eqnarray}となり、選択肢2が一番近いことがわかります。

なお、問題文中のヒントがなぜ成り立つかは、【標準】データの分散で説明しています。

解答

タチ：64
ツ：2