センター試験 数学I・数学A 2020年度追試 第1問 [2] 解説

【必答問題】

問題編

問題

　$a$ を定数とする。実数 $x$ に関する二つの条件 $p,q$ を次のように定める。

　$p:$ $-1\leqq x\leqq 3$
　$q:|x-a|\gt 3$

　条件 $p,q$ の否定をそれぞれ $\bar{p}$, $\bar{q}$ で表す。

(1) 命題「 $p\implies q$ 」が真であるような $a$ の値の範囲は\[ a\lt\myBox{ソタ},\ \myBox{チ}\lt a \]である。

(2) $a=\mybox{チ}$ のとき、 $x=\myBox{ツ}$ は命題「 $p\implies q$ 」の反例である。

(3) 実数 $x$ に関する条件 $r$ を次のように定める。

　$r:$ $3\lt x\leqq 4$

　次の $\mybox{テ}$ に当てはまるものを、下の 0 ～ 3 のうちから一つ選べ。

　$a=1$ のとき、条件「 $\bar{p}$ かつ $\bar{q}$ 」は条件 $r$ であるための $\myBox{テ}$ 。

　0: 必要条件であるが、十分条件ではない
　1: 十分条件であるが、必要条件ではない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

考え方

式のまま考えていくのは難しいので、数直線を書いて考えましょう。集合と命題との対応を考えて解いていきましょう。

【必答問題】

解答編

問題

　$a$ を定数とする。実数 $x$ に関する二つの条件 $p,q$ を次のように定める。

　$p:$ $-1\leqq x\leqq 3$
　$q:|x-a|\gt 3$

　条件 $p,q$ の否定をそれぞれ $\bar{p}$, $\bar{q}$ で表す。

(1) 命題「 $p\implies q$ 」が真であるような $a$ の値の範囲は\[ a\lt\myBox{ソタ},\ \myBox{チ}\lt a \]である。

解説

条件 $q$ は「 $x-a\lt -3$ または $x-a\gt 3$ 」と同値であり、「 $x\lt a-3$ または $x\gt a+3$ 」と同値です。

条件 $p$ を満たすときに条件 $q$ が満たされる場合を考えましょう。

条件 $p$ を満たすときに $x\lt a-3$ が成り立つ場合を考えましょう。こうなるのは $a-3$ が $3$ より大きいときです。

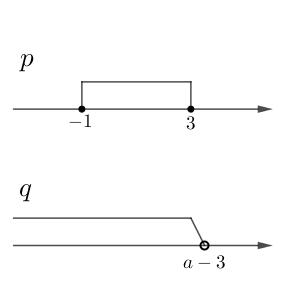
これ以外は $p$ を満たす範囲が $q$ を満たす範囲に含まれません。

次に、条件 $p$ を満たすときに $x\gt a+3$ が成り立つ場合を考えましょう。こうなるのは $a+3$ が $-1$ より小さいときです。

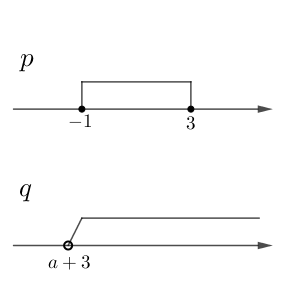
これ以外は $p$ を満たす範囲が $q$ を満たす範囲に含まれません。

以上から、条件 $p$ を満たすときに条件 $q$ が満たされるのは、「 $a-3\gt 3$ または $a+3\lt -1$ 」、つまり、「 $a\lt -4$ または $a\gt 6$ 」が成り立つときで、これ以外にはありません。

解答

ソタ：-4
チ：6

解答編 つづき

問題

(2) $a=\mybox{チ}$ のとき、 $x=\myBox{ツ}$ は命題「 $p\implies q$ 」の反例である。

解説

$a=6$ のとき、条件 $q$ は「 $x\lt 3$ または $x\gt 9$ 」と同値です。 $p$ を満たしているのにこれを満たしていないものは $x=3$ です。よって、これが反例です。

解答

ツ：3

解答編 つづき

問題

(3) 実数 $x$ に関する条件 $r$ を次のように定める。

　$r:$ $3\lt x\leqq 4$

　次の $\mybox{テ}$ に当てはまるものを、下の 0 ～ 3 のうちから一つ選べ。

　$a=1$ のとき、条件「 $\bar{p}$ かつ $\bar{q}$ 」は条件 $r$ であるための $\myBox{テ}$ 。

　0: 必要条件であるが、十分条件ではない
　1: 十分条件であるが、必要条件ではない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

解説

$a=1$ のとき、条件 $q$ は「 $x\lt -2$ または $x\gt 4$ 」と同値です。なので、 $\bar{q}$ は「 $-2\leqq x\leqq 4$ 」と同値です。

$\bar{p}$ は「 $x\lt -1$ または $x\gt 3$ 」と同値なので、「 $\bar{p}$ かつ $\bar{q}$ 」は「 $-2\leqq x\lt -1$ または $3\lt x\leqq 4$ 」と同値です。

このことから、条件 $r$ を満たせば、条件「 $\bar{p}$ かつ $\bar{q}$ 」も満たされますが、逆は成り立ちません。そのため、条件「 $\bar{p}$ かつ $\bar{q}$ 」は条件 $r$ であるための必要条件だが十分条件ではないことがわかります。

解答

テ：0