センター試験 数学I・数学A 2016年度追試 第5問 解説
問題編
問題
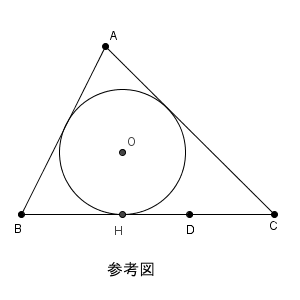
$\triangle \mathrm{ ABC }$ の内心を O, 内接円 O と辺 BC の接点を H とする。辺 BC 上に点 D をとる。ただし、 D は B, C と異なる点とする。
$\triangle \mathrm{ ABD }$ の内心を P とし、内接円 P と辺 BD の接点を E とする。 $\triangle \mathrm{ ACD }$ の内心を Q とし、内接円 Q と辺 CD の接点を F とする。
PQ を直径とする円と2点 D, H の間の関係で $\triangle \mathrm{ ABC }$ がどのような形でも成り立つものを調べる。次の $\mybox{オ}$ には、下の 0 ~ 3 のうちから当てはまるものを一つ選べ。
$\displaystyle \angle \mathrm{ ADP }=\frac{\myBox{ア}}{\myBox{イ}}\angle \mathrm{ ADB }$, $\displaystyle \angle \mathrm{ ADQ }=\frac{\myBox{ウ}}{\myBox{エ}}\angle \mathrm{ ADC }$ であるから、 PQ を直径とする円と点 D の関係について正しい選択肢は $\myBox{オ}$ である。0: D が辺 BC 上のどの位置にあっても、 D はその円の内部にある。
1: D が辺 BC 上のどの位置にあっても、 D はその円周上である。
2: D が辺 BC 上のどの位置にあっても、 D はその円の外部にある。
3: D が辺 BC 上のどの位置にあるかに応じて、 D は、円の内部、円周上、円の外部のどの場合もある。
次の $\mybox{カ}$ ~ $\mybox{サ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
\begin{eqnarray} \mathrm{ BH } &=& \frac{1}{2} (\mathrm{ AB }+\myBox{カ}-\myBox{キ}) \quad \cdots ① \\[5pt] \mathrm{ BE } &=& \frac{1}{2} (\mathrm{ AB }+\myBox{ク}-\myBox{ケ}) \quad \cdots ② \\[5pt] \mathrm{ DF } &=& \frac{1}{2} (\mathrm{ CD }+\myBox{コ}-\myBox{サ}) \quad \cdots ③ \\[5pt] \end{eqnarray}である。0: AC 1: AD 2: BC 3: BD
次の $\mybox{シ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
① ~ ③ から、 $\mathrm{ EH }=\myBox{シ}$ であることがわかる。
0: FQ 1: OP 2: $\frac{1}{2}$EP 3: DF
次の $\mybox{ス}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
PQ の中点を J とする。 J を通り辺 BC に垂直な直線と BC の交点を K とすると、 K は EF の中点であるから、 $\mathrm{ HK }=\myBox{ス}$ である。
0: DK 1: $\frac{1}{2}$JK 2: EH 3: $\frac{1}{2}$FK
次の $\mybox{セ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
$\mathrm{ HK }=\mybox{ス}$ に着目すると、 PQ を直径とする円と点 H の関係について、正しい選択肢は $\myBox{セ}$ である。
0: D が辺 BC 上のどの位置にあっても、 H はその円の内部にある。
1: D が辺 BC 上のどの位置にあっても、 H はその円周上である。
2: D が辺 BC 上のどの位置にあっても、 H はその円の外部にある。
3: D が辺 BC 上のどの位置にあるかに応じて、 H は、円の内部、円周上、円の外部のどの場合もある。
考え方
出てくる点が多く、考えにくいです。設問によって考えるべき点が異なるので、何度か図をかきなおしながら解くといいでしょう。
カ~サは、1つ解けたら使いまわすようにしましょう。終盤で出てくる J は円の中心であることに注意します。
解答編
問題
$\triangle \mathrm{ ABC }$ の内心を O, 内接円 O と辺 BC の接点を H とする。辺 BC 上に点 D をとる。ただし、 D は B, C と異なる点とする。
$\triangle \mathrm{ ABD }$ の内心を P とし、内接円 P と辺 BD の接点を E とする。 $\triangle \mathrm{ ACD }$ の内心を Q とし、内接円 Q と辺 CD の接点を F とする。
PQ を直径とする円と2点 D, H の間の関係で $\triangle \mathrm{ ABC }$ がどのような形でも成り立つものを調べる。次の $\mybox{オ}$ には、下の 0 ~ 3 のうちから当てはまるものを一つ選べ。
$\displaystyle \angle \mathrm{ ADP }=\frac{\myBox{ア}}{\myBox{イ}}\angle \mathrm{ ADB }$, $\displaystyle \angle \mathrm{ ADQ }=\frac{\myBox{ウ}}{\myBox{エ}}\angle \mathrm{ ADC }$ であるから、 PQ を直径とする円と点 D の関係について正しい選択肢は $\myBox{オ}$ である。0: D が辺 BC 上のどの位置にあっても、 D はその円の内部にある。
1: D が辺 BC 上のどの位置にあっても、 D はその円周上である。
2: D が辺 BC 上のどの位置にあっても、 D はその円の外部にある。
3: D が辺 BC 上のどの位置にあるかに応じて、 D は、円の内部、円周上、円の外部のどの場合もある。
解説
まずは図をかきましょう。
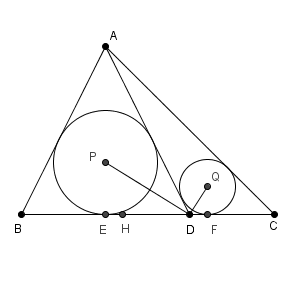
この問題では円 O は使わないので消しています。
P は $\triangle \mathrm{ ABD }$ の内心なので、\[ \angle \mathrm{ ADP }=\frac{1}{2}\angle \mathrm{ ADB } \]となります。また、同様にして\[ \angle \mathrm{ ADQ }=\frac{1}{2}\angle \mathrm{ ADC } \]もわかります。
この2つから
\begin{eqnarray}
\angle \mathrm{ PDQ }
&=&
\angle \mathrm{ ADP } +\angle \mathrm{ ADQ } \\
&=&
\frac{1}{2} (\angle \mathrm{ ADB } +\angle \mathrm{ ADC } ) \\
&=&
90^{\circ}
\end{eqnarray}が得られます。このことから、 D は PQ を直径とする円周上にあることがわかります。
解答
アイ:12
ウエ:12
オ:1
解答編 つづき
問題
次の $\mybox{カ}$ ~ $\mybox{サ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
\begin{eqnarray} \mathrm{ BH } &=& \frac{1}{2} (\mathrm{ AB }+\myBox{カ}-\myBox{キ}) \quad \cdots ① \\[5pt] \mathrm{ BE } &=& \frac{1}{2} (\mathrm{ AB }+\myBox{ク}-\myBox{ケ}) \quad \cdots ② \\[5pt] \mathrm{ DF } &=& \frac{1}{2} (\mathrm{ CD }+\myBox{コ}-\myBox{サ}) \quad \cdots ③ \\[5pt] \end{eqnarray}である。0: AC 1: AD 2: BC 3: BD
解説
まずは、 BH から考えます。
円 O と AB, ACとの接点をそれぞれ S, T と置きます。
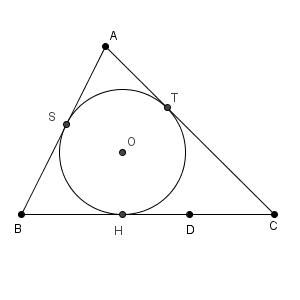
ここで、円 O が内接円なので、 $\mathrm{ BH }=\mathrm{ BS }$ などが成り立つことを用いて
\begin{eqnarray}
\mathrm{ BH }
&=&
\mathrm{ BC } -\mathrm{ CH } \\
&=&
\mathrm{ BC } -\mathrm{ CT } \\
&=&
\mathrm{ BC } -(\mathrm{ AC }-\mathrm{ AT }) \\
&=&
\mathrm{ BC } -\mathrm{ AC }+\mathrm{ AS } \\
&=&
\mathrm{ BC } -\mathrm{ AC }+ (\mathrm{ AB }-\mathrm{ BS }) \\
&=&
\mathrm{ BC } -\mathrm{ AC }+ \mathrm{ AB }-\mathrm{ BH } \\
\end{eqnarray}が成り立つので、
\begin{eqnarray}
2\mathrm{ BH } &=& \mathrm{ BC } -\mathrm{ AC }+ \mathrm{ AB } \\
\mathrm{ BH } &=& \frac{1}{2} (\mathrm{ AB }+\mathrm{ BC } -\mathrm{ AC }) \\
\end{eqnarray}が成り立ちます。
同じように考えれば他も求められます。

上の結果より BH を含む辺を足し、含まない辺を引いていることがわかるので、対応を考えると、
\begin{eqnarray}
\mathrm{ BE } &=& \frac{1}{2} (\mathrm{ AB }+\mathrm{ BD } -\mathrm{ AD }) \\[5pt]
\mathrm{ DF } &=& \frac{1}{2} (\mathrm{ CD }+\mathrm{ AD } -\mathrm{ AC }) \\[5pt]
\end{eqnarray}となります。
解答
カキ:20
クケ:31
コサ:10
解答編 つづき
問題
次の $\mybox{シ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
① ~ ③ から、 $\mathrm{ EH }=\myBox{シ}$ であることがわかる。
0: FQ 1: OP 2: $\frac{1}{2}$EP 3: DF

①と②より
\begin{eqnarray}
\mathrm{ EH }
&=&
\mathrm{ BH }-\mathrm{ BE } \\[5pt]
&=&
\frac{(\mathrm{ AB }+\mathrm{ BC } -\mathrm{ AC })-(\mathrm{ AB }+\mathrm{ BD } -\mathrm{ AD })}{2} \\[5pt]
&=&
\frac{ \mathrm{ BC }-\mathrm{ BD } +\mathrm{ AD } -\mathrm{ AC } }{2} \\[5pt]
\end{eqnarray}となります。 $\mathrm{ BC }-\mathrm{ BD }$ は CD と一致するので、③からこの式は DF と一致することがわかります。
解答
シ:3
解答編 つづき
問題
次の $\mybox{ス}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
PQ の中点を J とする。 J を通り辺 BC に垂直な直線と BC の交点を K とすると、 K は EF の中点であるから、 $\mathrm{ HK }=\myBox{ス}$ である。
0: DK 1: $\frac{1}{2}$JK 2: EH 3: $\frac{1}{2}$FK
解説
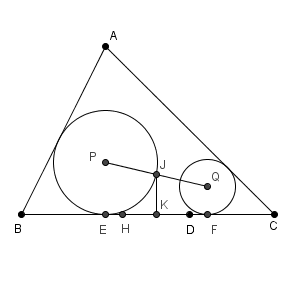
K は EF の中点になるので、 $\mathrm{ EK }=\mathrm{ FK }$ が成り立ちます。これと先ほど求めた $\mathrm{ EH }=\mathrm{ DF }$ を用いれば、
\begin{eqnarray}
\mathrm{ HK }
&=&
\mathrm{ EK }-\mathrm{ EH } \\
&=&
\mathrm{ FK }-\mathrm{ DF } \\
&=&
\mathrm{ DK } \\
\end{eqnarray}が得られます。
解答
ス:0
次の $\mybox{セ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
$\mathrm{ HK }=\mybox{ス}$ に着目すると、 PQ を直径とする円と点 H の関係について、正しい選択肢は $\myBox{セ}$ である。
0: D が辺 BC 上のどの位置にあっても、 H はその円の内部にある。
1: D が辺 BC 上のどの位置にあっても、 H はその円周上である。
2: D が辺 BC 上のどの位置にあっても、 H はその円の外部にある。
3: D が辺 BC 上のどの位置にあるかに応じて、 H は、円の内部、円周上、円の外部のどの場合もある。
解説

見方を変えると J は PQ を直径とする円の中心であることがわかります。また、$\mathrm{ HK }=\mathrm{ DK }$ より $\triangle \mathrm{ JKH }$ と $\triangle \mathrm{ JKD }$ は合同になります。よって、 $\mathrm{ JH }=\mathrm{ JD }$ です。 D はこの円周上にあるので、 H も同じくこの円周上にあることがわかります。
解答
セ:1