センター試験 数学I・数学A 2016年度追試 第2問 [4] 解説
問題編
問題
(注:一部表記を調整しています)次の表3は、あるクラスの生徒30人に行った科目Xと科目Yのテストの得点であり、これらの平均値、標準偏差、共分散をまとめたものが下の表4である。
表3 科目Xと科目Yの得点
\begin{array}{cccccccccccccccc} \hline \textsf{科目X} & 63 & 76 & 58 & 71 & 75 & 56 & 81 & 80 & 84 & 77 & 76 & 63 & 63 & 59 & 63 \\ \textsf{科目Y} & 47 & 78 & 60 & 46 & 58 & 63 & 73 & 59 & 66 & 49 & 62 & 58 & 65 & 50 & 42 \\ \hline \end{array}\begin{array}{cccccccccccccccc} \hline \textsf{科目X} & 77 & 78 & 68 & 59 & 72 & 68 & 79 & 67 & 79 & 73 & 77 & 67 & 63 & 78 & 76 \\ \textsf{科目Y} & 82 & 66 & 40 & 55 & 42 & 69 & 77 & 57 & 63 & 52 & 49 & 45 & 55 & 84 & 56 \\ \hline \end{array}表4
平均値 標準偏差 科目X 70.9 7.81 科目Y 58.9 11.74 (共分散とは、科目Xの得点の偏差と科目Yの得点の偏差の積の平均値である)
科目Xと科目Yの得点の共分散 36.89 (1) 次の $\mybox{ソ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
科目Xと科目Yの得点を散布図にしたものは $\myBox{ソ}$ である。
0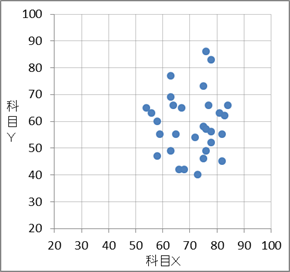
1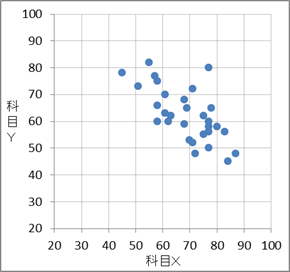
2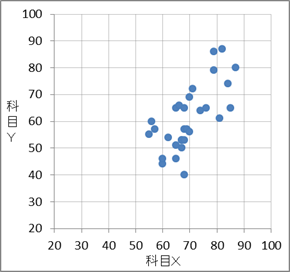
3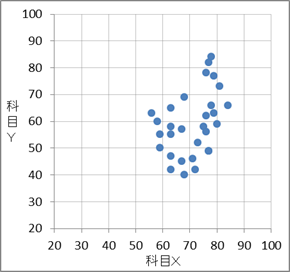
(2) 次の $\mybox{タ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
表3の得点を $\displaystyle \frac{1}{2}$ にして50点満点の得点に換算した。例えば、62点であった場合は得点を2で割った値である31点とし、63点であった場合は31.5点とする。このとき、科目Xの得点の偏差と科目Yの得点の偏差は、換算後、それぞれもとの得点の偏差の $\displaystyle \frac{1}{2}$ になる。したがって、科目Xについてもとの標準偏差と換算後の標準偏差を比較し、さらにもとの共分散と換算後の共分散を比較すると、 $\myBox{タ}$ 。
0 換算後の標準偏差と共分散の値はともに、もとの値の $\displaystyle \frac{1}{2}$ になる
1 換算後の標準偏差と共分散の値はともに、もとの値の $\displaystyle \frac{1}{4}$ になる
2 換算後の標準偏差の値はもとの値の $\displaystyle \frac{1}{2}$ になり、共分散の値はもとの値の $\displaystyle \frac{1}{4}$ になる
3 換算後の標準偏差の値はもとの値の $\displaystyle \frac{1}{4}$ になり、共分散の値はもとの値の $\displaystyle \frac{1}{2}$ になる
考え方
(1)は相関係数からあたりをつけて考えましょう。答えを出すだけなら、各値に対応する点があるかどうかで判断することも可能ですが。
(2)は、標準偏差や共分散をどうやって求めるか、定義を思い出して考えましょう。
解答編
問題
(注:一部表記を調整しています)
次の表3は、あるクラスの生徒30人に行った科目Xと科目Yのテストの得点であり、これらの平均値、標準偏差、共分散をまとめたものが下の表4である。
表3 科目Xと科目Yの得点
\begin{array}{cccccccccccccccc} \hline \textsf{科目X} & 63 & 76 & 58 & 71 & 75 & 56 & 81 & 80 & 84 & 77 & 76 & 63 & 63 & 59 & 63 \\ \textsf{科目Y} & 47 & 78 & 60 & 46 & 58 & 63 & 73 & 59 & 66 & 49 & 62 & 58 & 65 & 50 & 42 \\ \hline \end{array}\begin{array}{cccccccccccccccc} \hline \textsf{科目X} & 77 & 78 & 68 & 59 & 72 & 68 & 79 & 67 & 79 & 73 & 77 & 67 & 63 & 78 & 76 \\ \textsf{科目Y} & 82 & 66 & 40 & 55 & 42 & 69 & 77 & 57 & 63 & 52 & 49 & 45 & 55 & 84 & 56 \\ \hline \end{array}表4
平均値 標準偏差 科目X 70.9 7.81 科目Y 58.9 11.74 (共分散とは、科目Xの得点の偏差と科目Yの得点の偏差の積の平均値である)
科目Xと科目Yの得点の共分散 36.89 (1) 次の $\mybox{ソ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
科目Xと科目Yの得点を散布図にしたものは $\myBox{ソ}$ である。
0
1
2
3
解説
まず、共分散が正であることから、散布図は右肩上がりになることがわかります。右肩下がりになっている 1 が正しくないことがわかります。
次に、相関係数を考えてみます。標準偏差と共分散を使って、次のように求めることができます。\[ \frac{36.89}{ 7.81\times 11.74 }=0.402\cdots \]これから、相関はそれほど強くないことがわかります。なので、 2 ではないだろうと予想できます。また、 0 は右下の方にも点が集まっていて全体的に丸く分布しているので、相関係数は 0.4 よりもっと小さいのではないかと予想できます。
答えが 3 だとあたりをつけ、これを確かめるために特徴的な値で確認してみましょう。1 以外の散布図で 3 だけが持つ特徴として、「科目Xの80点台の人数」があります。 0 も 2 も80点台は5人いますが、 3 は3人です。実際、表3を見てみると、80点台は「81, 80, 84」の3人しかいません。そのため、答えは 3 で間違いないことがわかります。
(一番初めの値「63, 47」だけでも 3 ではないかと推測できますが。)
解答
ソ:3
参考
解答編 つづき
問題
(2) 次の $\mybox{タ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
表3の得点を $\displaystyle \frac{1}{2}$ にして50点満点の得点に換算した。例えば、62点であった場合は得点を2で割った値である31点とし、63点であった場合は31.5点とする。このとき、科目Xの得点の偏差と科目Yの得点の偏差は、換算後、それぞれもとの得点の偏差の $\displaystyle \frac{1}{2}$ になる。したがって、科目Xについてもとの標準偏差と換算後の標準偏差を比較し、さらにもとの共分散と換算後の共分散を比較すると、 $\myBox{タ}$ 。
0 換算後の標準偏差と共分散の値はともに、もとの値の $\displaystyle \frac{1}{2}$ になる
1 換算後の標準偏差と共分散の値はともに、もとの値の $\displaystyle \frac{1}{4}$ になる
2 換算後の標準偏差の値はもとの値の $\displaystyle \frac{1}{2}$ になり、共分散の値はもとの値の $\displaystyle \frac{1}{4}$ になる
3 換算後の標準偏差の値はもとの値の $\displaystyle \frac{1}{4}$ になり、共分散の値はもとの値の $\displaystyle \frac{1}{2}$ になる
解説
標準偏差は、「偏差を2乗したものを足してルートをとったもの」です。そのため、偏差が $\displaystyle \frac{1}{2}$ になると、標準偏差も $\displaystyle \frac{1}{2}$ となります。
共分散は、「科目Xの得点の偏差 と 科目Yの得点の偏差 の積をすべて足す」ことで求めることができます。偏差がそれぞれ $\displaystyle \frac{1}{2}$ になるため、積は $\displaystyle \frac{1}{4}$ となります。よって、共分散も元の値の $\displaystyle \frac{1}{4}$ となります。
解答
タ:2





