【標準】陰関数の微分と接線

🕒 2018/10/11 🔄 2023/06/26

ここでは、陰関数で表された曲線の接線について考えていきます。

📘 目次

陰関数の微分と接線

例題

曲線 $x^2+4y^2=25$ 上の点 $(3,2)$ における接線の方程式を求めなさい。

問題文中に出てきた曲線は、楕円ですね。 $y=f(x)$ の形ではなく、 $F(x,y)=0$ の形で表されているものを、陰関数と呼ぶのでした（参考：【基本】陰関数の微分（円の方程式と微分））。今の場合、\[ F(x,y)=x^2+4y^2-25 \]とすれば、陰関数であることがわかります。

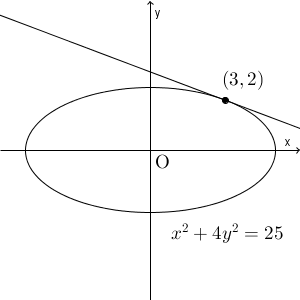
接線は、その点での微分係数が同じものなので、点 $(3,2)$ での微分係数を求めればいいことがわかります。陰関数の微分は、両辺を $x$ で微分して考えていけばいいのでしたね（参考：【標準】陰関数や媒介変数表示と微分）。両辺を微分して計算すると
\begin{eqnarray} 2x+4\cdot 2y\dfrac{dy}{dx} &=& 0 \\[5pt] \dfrac{dy}{dx} &=& -\frac{x}{4y} \\[5pt] \end{eqnarray}となります。これより、点 $(3,2)$ での微分係数は\[ -\frac{3}{4\cdot 2}=-\frac{3}{8} \]であることがわかるので、接線の方程式は \begin{eqnarray} y-2 &=& -\dfrac{3}{8}(x-3) \\[5pt] y &=& -\dfrac{3}{8}x+\frac{25}{8} \\[5pt] \end{eqnarray}となります。これが答えです。

なお、この問題では、接線の方から考えることもできます。つまり、接線を\[ y=m(x-3)+2 \]とおき、楕円の方程式に代入して、「 $x$ の二次方程式の判別式が $0$ 」とした条件から $m$ を求める、ということです。この方法は、楕円や双曲線のときには使えますが、三角関数や指数関数などが入ってきたりすると使えなくなってしまいます。微分を使う解き方のほうが、応用範囲が広くなります。

一般的な楕円の接線

先ほどは、楕円の接線を求めましたが、一般的な場合でも、楕円の接線を求めてみましょう。

楕円は、一般的には\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \]と書くことができます（参考：【基本】楕円の焦点（焦点がx軸上））。この楕円上の点 $(p,q)$ での接線を求めてみましょう。

まず、先ほどと同じように、両辺を微分して微分係数を求めてみましょう。なお、はじめのうちは、 $y\ne 0$ の場合を考えることにします。
\begin{eqnarray} \frac{2x}{a^2}+\frac{2y}{b^2}\cdot\dfrac{dy}{dx} &=& 0 \\[5pt] \dfrac{dy}{dx} &=& -\frac{x}{a^2}\cdot \frac{b^2}{y} \\[5pt] \end{eqnarray}となるので、点 $(p,q)$ での微分係数は\[ -\dfrac{p}{a^2}\cdot\frac{b^2}{q} \]となります。これが接線の傾きなので、接線の方程式は、どんどん変形していくと \begin{eqnarray} y-q &=& -\frac{p}{a^2}\cdot \frac{b^2}{q}(x-p) \\[5pt] \frac{q}{b^2}y-\frac{q^2}{b^2} &=& -\dfrac{p}{a^2}x+\dfrac{p^2}{a^2} \\[5pt] \dfrac{px}{a^2}+\frac{qy}{b^2} &=& \dfrac{p^2}{a^2}+\frac{q^2}{b^2} \\[5pt] \end{eqnarray}ここで、点 $(p,q)$ がこの楕円上の点であるから、最後の式の右辺は、 $1$ となるので、接線の方程式は\[ \dfrac{px}{a^2}+\frac{qy}{b^2}=1 \]と求められます。この式は、よく見ると、もとの楕円の方程式で、 $x,y$ をそれぞれ1つずつ $p,q$ に入れ替えたものとなっています。

また、 $y=0$ のときも考えましょう。接点が $(a,0)$ のときは、接線は $x=a$ となります。接線が $(-a,0)$ のときは、接線は $x=-a$ となります。どちらも上で導いた式で表されることがわかります。

楕円の接線の方程式

楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ の、接点 $(p,q)$ での接線の方程式は、次で表される。\[ \frac{px}{a^2}+\frac{qy}{b^2}=1 \]

これを用いて、先ほどの例題を考えてみましょう。楕円の方程式は\[ \frac{x^2}{25}+\frac{y^2}{\frac{25}{4} }=1 \]と書けるので、点 $(3,2)$ での接線は\[ \frac{3x}{25}+\frac{2y}{\frac{25}{4} }=1 \]となります。これを計算して $y=$ の形に変形すると
\begin{eqnarray} \frac{3x}{25}+\frac{8y}{25} &=& 1 \\[5pt] \frac{8}{25}y &=& -\frac{3x}{25}+1 \\[5pt] y &=& -\frac{3}{8}x+\frac{25}{8} \\[5pt] \end{eqnarray}となり、たしかに先ほどの答えと同じになります。

ちなみに、この内容は、【応用】二次曲線と接線で見た内容と同じです。リンク先では、二次曲線の1つとして楕円を挙げていますが、二次曲線の場合は、接線の方程式を代入して、「 $x$ の二次方程式が重解を持つ、判別式が $0$ になる」という条件から導くことができます。ただ、微分を使った方が、理屈は難しいですが、計算量自体は少なくなっていると思います。