🏠 Home / 数学III / 微分 / 微分と接線

【標準】媒介変数表示と接線

🕒 2018/10/12 🔄 2023/05/01

ここでは、媒介変数で表された曲線の接線について考えていきます。

📘 目次

媒介変数表示と接線

例題

曲線 $x=\theta-\sin\theta$, $y=1-\cos\theta$ の $\theta=\dfrac{\pi}{2}$ に対応する点での接線の方程式を求めなさい。

この曲線は、【基本】サイクロイドと媒介変数表示で見たように、サイクロイドといって、次のような曲線になります。

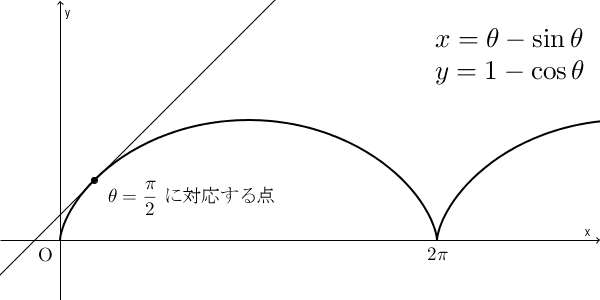
上のリンク先では、「円が直線に接しながら滑らずに回転するとき、円周上の定点が描く曲線をサイクロイドと呼びます」と書きました。

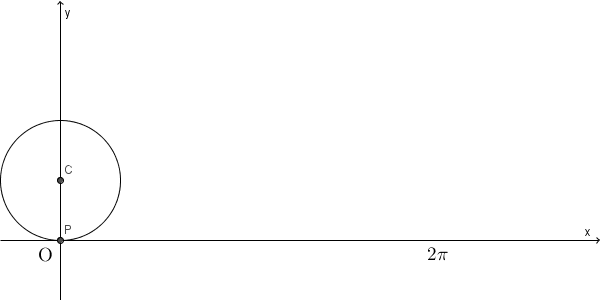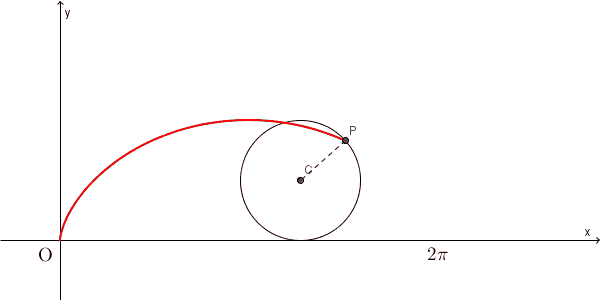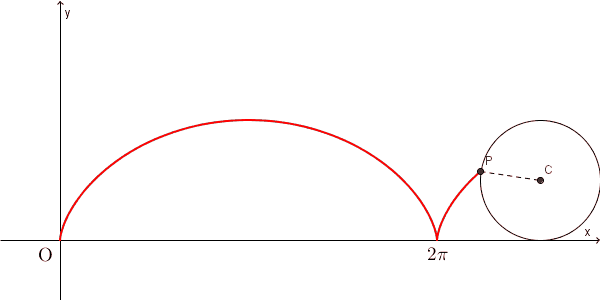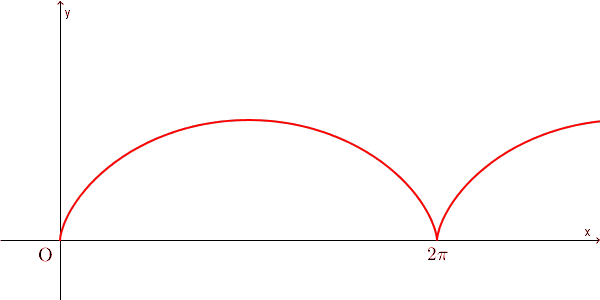
そして、その曲線は、問題文中にあるような、媒介変数で書ける、という話をしました。

ただ、逆に、この問題文中にあるような、媒介変数で表示された式を見て、「あ、これはサイクロイドだな」とか「このグラフはこういう形だったな」と思いつける人は少ないかもしれません。

でも、大丈夫です。今の場合は、この媒介変数表示からグラフがかけなくても、接線の方程式を求めることだけはできます。

ちなみにいうと、もう少し学習を進めていくと、このような媒介変数で表された式からグラフをかくこともできるようになります。今でも頑張れば、複数の点をかいて、線でつなげてグラフの概形をかくことはできますけども。

さて、それでは接線を考えていきます。

$\theta=\dfrac{\pi}{2}$ のときなので、まずは、このときの接点の座標を求めましょう。媒介変数表示された式に入れれば、\[ \left(\dfrac{\pi}{2}-1,1\right) \]であることがわかります。通る点の座標がわかったので、接線の方程式を求めるには、あとは接線の傾きが分かればいいですね。

この点での接線の傾きは、この点での微分係数を求めればいいです。媒介変数で表された式の場合、微分は次のようにして計算するのでした（参考：【基本】媒介変数表示と微分）。\[
\dfrac{dy}{dx}=\frac{\dfrac{dy}{dt} }{\dfrac{dx}{dt} } \]ここで、
\begin{eqnarray} \dfrac{dy}{dt}&=&\sin \theta \\[5pt] \dfrac{dx}{dt}&=&1-\cos \theta \\[5pt] \end{eqnarray}なので、\[ \dfrac{dy}{dx}=\frac{\sin \theta}{1-\cos \theta} \]となります。ここに $\theta=\dfrac{\pi}{2}$ を代入すれば、接線の傾きが $1$ であることがわかります。

通る点と傾きがわかったので、接線の方程式は
\begin{eqnarray} y-1&=& 1\cdot \left(x-\dfrac{\pi}{2}+1\right) \\[5pt] y&=& x+2-\dfrac{\pi}{2} \\[5pt] \end{eqnarray}となります。これが答えです。