【標準】2曲線の共通接線と微分

🕒 2018/10/14 🔄 2023/06/26

ここでは、2つの曲線の両方に接するような直線を求める問題を考えていきます。

📘 目次

2曲線の共通接線

例題

2つの曲線 $y=e^x-2$ と $y=\log x$ の両方に接する直線の方程式を求めなさい。

この例題のように、両方の曲線に接する直線のことを、共通接線といいます。この例題は、共通接線を求めなさい、という問題です。

【標準】通る点から接線の方程式を求めるでも見た通り、接線を考えるには、接点の座標と、その点での直線の傾き、つまり微分係数を考えればいいのでした。【標準】接する2つの曲線と微分では、「接点が共通」という状況だったので、接点の座標を文字で置いて考えていけばよかったのですが、今回は接点が共通とは限りません。実際、2つの曲線は共有点を持たないので、接点は共通ではありません。

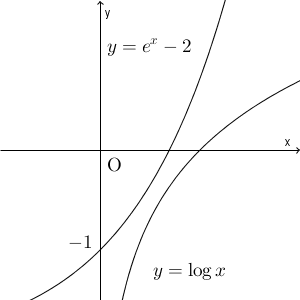
こういう状況でも、接点の座標と微分係数を使いたいので、それぞれの接点の座標を文字で置いて考えることになります。

まず、 $f(x)=e^x-2$, $g(x)=\log x$ とおきます。このとき、 $f'(x)=e^x$, $g'(x)=\dfrac{1}{x}$ となります。

よって、 $y=f(x)$ の $x=s$ での接線の方程式は\[ y-(e^s-2)=e^s(x-s) \]となります。また、 $y=g(x)$ の $x=t$ $(t\gt 0)$ での接線の方程式は\[ y-\log t=\frac{1}{t}(x-t) \]となります。この両方の接線が一致するとき、その直線は2つの曲線に接することがわかります。

まず、傾きが同じという条件から\[ e^s=\frac{1}{t} \]となることがわかります。これを2つ目の接線の方程式に代入すると
\begin{eqnarray} y-\log e^{-s} &=& e^s(x-e^{-s}) \\[5pt] y &=& e^s x -s-1 \\[5pt] \end{eqnarray}となります。また、1つ目の接線の方程式を変形すると \begin{eqnarray} y-(e^s-2)=e^s(x-s) \\[5pt] y=e^s x -e^s s+e^s-2 \\[5pt] \end{eqnarray}となります。この2つの直線の切片が等しいとすると \begin{eqnarray} -s-1 &=& -e^s s+e^s-2 \\[5pt] e^s s -e^s -s+1 &=& 0 \\[5pt] (e^s-1)(s-1) &=& 0 \\[5pt] s &=& 0,1 \end{eqnarray}となります。 $t=e^{-s}$ なので、 $t\gt 0$ が成り立つので、どちらも解となります。接線の方程式は\[ y=x-1,\ y=ex-2 \]となります。

【標準】接する2つの曲線と微分と似ていますが、接点が共通かそうじゃないか、という違いがあります。リンク先の問題では、接点が共通でしたが、ここで考えた問題では接点が共通ではありませんでした。そのため、それぞれの接点を文字で置く必要があるので、 $(s,f(s))$, $(t,g(t))$ とおいて考えました。

共通接線に関する問題は、【応用】2つの円の共通接線の方程式や【標準】微分を利用して2つの放物線の共通接線を求めるで、すでに見ています。ただ、ここで考えた共通接線の問題は、これらのリンク先とは少し違う解き方をしています。

2つの円の共通接線を求める問題では、「片方の円の接線が、もう片方に接する場合を考える」としています。点と直線の距離の公式を使って、「円の中心からの距離が半径と同じなら、その直線は円と接する」と考えるわけですね。また、2つの放物線の共通接線を求める問題では、「片方の放物線の接線が、もう片方に接する場合を考える」という解き方をしています。判別式を使って接する場合を考えるわけです。

ただ、この例題では、「片方の曲線の接線が、もう片方の曲線に接する」という考え方はしていません。円や放物線の場合は、直線が接するかどうか、判別する方法があります（円なら中心との距離を、放物線なら判別式を使う）が、一般の場合には、そのようなものはありません。そのため、「それぞれの曲線の接線の方程式を考えて、それらが一致する場合を考える」という解き方になります。