【基本】微分と接線・法線の方程式

ここでは、微分係数を用いて、接線と法線の方程式を見ていきます。

接線の方程式

微分係数を用いて接線の方程式を求める方法は、【基本】微分と接線の方程式でも見ました。リンク先では三次関数の場合を考えていますが、ここでは、別の関数で考えてみましょう。

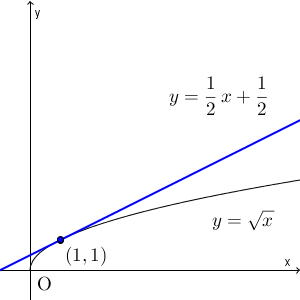
$y=\sqrt{x}$ について考えます。このとき、点 $(1,1)$ と、この点に近づいていく $(p,\sqrt{p})$ について考えてみましょう。この2点を結ぶ直線は、次のように変化します。（直線が見やすくなるように、この図だけ縦と横の縮尺を変えています）

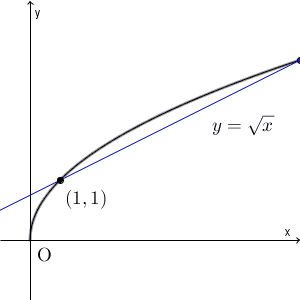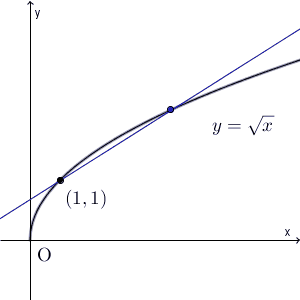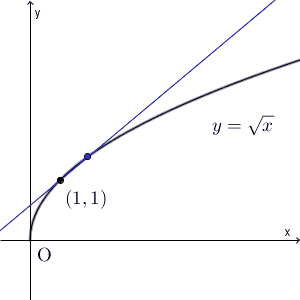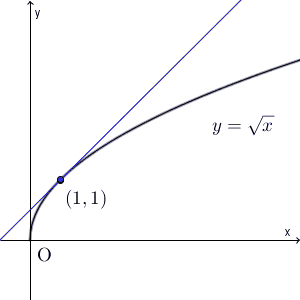
これを見ると、最終的には、ある直線に近づいていくことがわかります。その直線は $(1,1)$ を通ることはわかりますが、問題は傾きですね。傾きは、次のような極限で表すことができます。\[ \lim_{p\to 1} \frac{\sqrt{p}-1}{p-1} \]これは、関数 $y=\sqrt{x}$ の $x=1$ での微分係数です。微分係数の定義そのままですね。この関数を微分すると、\[ \frac{dy}{dx}=\frac{1}{2\sqrt{x} } \]なので、 $x=1$ での微分係数は $\dfrac{1}{2}$ となります。このことから、次のような直線に近づいていくことがわかります。
\begin{eqnarray} y-1 &=& \frac{1}{2}(x-1) \\[5pt] y &=& \frac{1}{2}x+\frac{1}{2} \\[5pt] \end{eqnarray}となります。

このように、関数 $y=f(x)$ が $x=a$ で微分可能であるとき、 $p\to a$ としたときに、 $(a,f(a))$ と $(p,f(p))$ を結んだ直線が近づいていく先の直線のことを、接線(tangent) といいます。この接線の傾きは、 $f'(a)$ で表すことができるので、次のことが言えます。

定義からわかることですが、接線というのは、その点での微分係数が同じである直線、と考えることができます。

微分を学ぶ前から、接線という言葉は出てきました。円や放物線のところですね。

円や放物線を学んだときに出てきた接線は、共有点が1個しかない直線と説明されていました。ただ、微分を用いた接線の定義、つまり、曲線上の2点を結び、その2点を近づけていくときに得られる直線、という定義でも、同じ直線が得られることがわかるでしょう。

微分について学んでいくと、計算によって、微分を使って定義した接線が共有点を1個しか持たないことも確かめられるようになります。つまり、微分を使った新しい定義は今までの接線の定義を拡張したものである、ということです。この新しい定義によって、よりたくさんの曲線に対して、接線を考えられるようになります。

接線は、「その点のまわりでは、グラフにすごく近い直線」と考えられます。そのため、もとの関数のグラフをかくため、増減を調べるために、接線の傾き（微分係数）の情報を利用する、といった使い方を今後はしていきます。（三次関数のときにも一度やっていますが）

法線の方程式

曲線 $y=f(x)$ 上のある点A $(a,f(a))$ での接線 $\ell$ を考えたときに、点A を通り、接線 $\ell$ に垂直な直線を、法線(normal) といいます。

例えば、 $y=\sqrt{x}$ の $(1,1)$ での法線は、次の青い太線のようになります。

法線が出てくる場面は、接線に比べるとだいぶ少ないですが、直線の性質を考えれば方程式を求めるのはそれほど難しくありません。通る点がわかっているので、あとは傾きが分かればいいですね。垂直に交わる2直線の傾きの積は $-1$ です（参考：【基本】垂直な直線の方程式）。また、接線の傾きは $f'(x)$ なので、法線の方程式は次のように書くことができます。

例えば、冒頭の $y=\sqrt{x}$ の例で考えてみます。点 $(1,1)$ での法線の方程式を求めるには、まず接線の傾きを求めます。そのためにまずは関数を微分して、\[ y'=\frac{1}{2\sqrt{x} } \]と計算します。これから、接線の傾きが $\dfrac{1}{2}$ であることを求め、法線の傾きが $-2$ であることを求めます。これより、
\begin{eqnarray} y-1 &=& -2(x-1) \\[5pt] y &=& -2x+3 \\[5pt] \end{eqnarray}が法線の方程式となります。

おわりに

ここでは、微分係数を用いて、接線や法線の方程式がどのように表されるかを見ました。傾きを計算するときに、微分の計算が必要となるので、基本的な微分の計算はできるようになっておきましょう。