【標準】定積分の置換積分（三角関数：cosθやsinθを使う）

🕒 2018/12/05 🔄 2023/05/01

ここでは、定積分の置換積分で、 $\cos\theta$ や $\sin\theta$ を使って置換するものを見ていきます。

📘 目次

cosを使った定積分の置換積分

例題

次の定積分を計算しなさい。\[ \int_0^1 \sqrt{4-x^2} dx \]

置換積分を使おうと、 $u=4-x^2$ や $u=\sqrt{4-x^2}$ と置きたくなりますが、ここでは、別の置き方を考えます。

この被積分関数はどんな関数なのかを少し考えてみましょう。 $y=\sqrt{4-x^2}$ を変形すると $x^2+y^2=4$ となることから、原点が中心で半径が $2$ の円であることがわかります。なので、 $y=\sqrt{4-x^2}$ はこの円の一部であることがわかります。

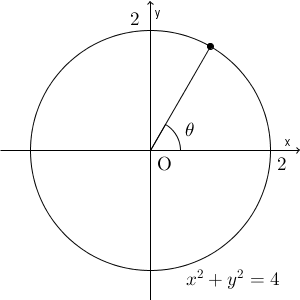
これより、三角比・三角関数のところで使ったような $x=2\cos\theta$ という置き方（ $0\leqq x\lt 2\pi$ ）を考えてみましょう。この $2$ は半径を表しています。 $\theta$ は、点 $(2,0)$ を原点を中心として反時計回りにどれだけ回転するか、を表しています。

このように置くと、積分区間は、
\begin{array}{c|ccc} x & 0 & \cdots & 1 \\ \hline \theta & \frac{\pi}{2} & \cdots & \frac{\pi}{3} \\ \end{array}となります。 $x$ が $0$ から $1$ まで変化するように $2\cos\theta$ を動かすには $\theta$ を $\dfrac{\pi}{2}$ から $\dfrac{\pi}{3}$ へと変化させればいいです。なお、 $\theta=\dfrac{3}{2}\pi$ のときも $x=0$ となりますが、 $\dfrac{3}{2}\pi$ から $\dfrac{\pi}{3}$ へ変化させると、 $x$ は $0$ から $-2$ になった後に $1$ となり、元の積分区間の「 $0$ から $1$ 」と対応が一致しないので、 $\dfrac{3}{2}\pi$ は採用せずに $\dfrac{\pi}{2}$ を採用しています。

さて、上のように $\frac{\pi}{2}$ から $\frac{\pi}{3}$ へと変化するように対応させると、このときの被積分関数は、\[ \sqrt{4-4\cos^2 \theta}=2\sin \theta \]となります。また、 $dx$ を $-2\sin \theta d\theta$ で置き換えればいいので、
\begin{eqnarray} & & \int_0^1 \sqrt{4-x^2} dx \\[5pt] &=& \int_{\frac{\pi}{2} }^{\frac{\pi}{3} } 2\sin \theta \cdot (-2\sin\theta)d\theta \\[5pt] &=& \int_{\frac{\pi}{3} }^{\frac{\pi}{2} } 4\sin^2 \theta d\theta \\[5pt] &=& \int_{\frac{\pi}{3} }^{\frac{\pi}{2} } 2(1-\cos 2\theta) d\theta \\[5pt] &=& \Big[ 2\theta-\sin 2\theta \Big]_{\frac{\pi}{3} }^{\frac{\pi}{2} } \\[5pt] &=& \left(\pi-0\right) -\left(\frac{2}{3}\pi-\frac{\sqrt{3} }{2}\right) \\[5pt] &=& \frac{1}{3}\pi +\frac{\sqrt{3} }{2} \\[5pt] \end{eqnarray}となります。これが答えです。

ところで、この積分は、図形的に何を表しているのかを考えてみましょう。【基本】定積分の復習で見た、面積との関係を踏まえると、この定積分は、 $y=\sqrt{4-x^2}$ と $x=0$, $x=1$ と $x$ 軸で囲まれた部分の面積と等しくなります。

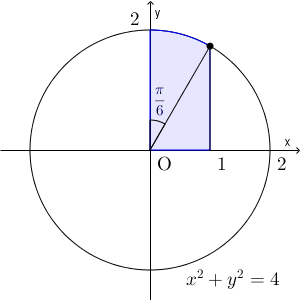
上の図からもわかる通り、これは、半径 $2$ で中心角が30度のおうぎ形の面積と、底辺が $1$ で高さが $\sqrt{3}$ の直角三角形の面積の和です。こういわれれば、中学生でもできる内容ですね。この面積の和が上で求めた定積分と一致していることが確認できます。

積分区間の対応について

積分区間の対応は、値の変化が同じようになれば、別の対応のさせ方でも構いません。先ほどは、 $\dfrac{3}{2}\pi$ から $\dfrac{\pi}{3}$ とするのは $x$ の対応と違う値をとってしまうのでダメでしたが、次のようにすれば問題ありません。
\begin{array}{c|ccc} x & 0 & \cdots & 1 \\ \hline \theta & \frac{3}{2}\pi & \cdots & \frac{5}{3}\pi \\ \end{array}このように対応させると、この範囲では、被積分関数は\[ \sqrt{4-4\cos^2 \theta}=-2\sin \theta \]となるので、 \begin{eqnarray} & & \int_0^1 \sqrt{4-x^2} dx \\[5pt] &=& \int_{\frac{3\pi}{2} }^{\frac{5\pi}{3} } (-2\sin \theta) \cdot (-2\sin\theta)d\theta \\[5pt] &=& \int_{\frac{3\pi}{2} }^{\frac{5\pi}{3} } 4\sin^2 \theta d\theta \\[5pt] &=& \int_{\frac{3\pi}{2} }^{\frac{5\pi}{3} } 2(1-\cos 2\theta) d\theta \\[5pt] &=& \Big[ 2\theta-\sin 2\theta \Big]_{\frac{3\pi}{2} }^{\frac{5\pi}{3} } \\[5pt] &=& \left(\frac{10}{3}\pi+\frac{\sqrt{3} }{2}\right) -\left(3\pi-0\right) \\[5pt] &=& \frac{1}{3}\pi +\frac{\sqrt{3} }{2} \\[5pt] \end{eqnarray}となって、先ほどと同じ結果になります。ただ、この計算からもわかる通り、計算が複雑になってしまうため、複数の対応のさせ方がある場合でも、普通は $0$ に近い正の値で対応させることがほとんどです。

sinを使った定積分の置換積分

また、この問題では、三角関数の場面でよく使う $x=\cos \theta$ を使いましたが、置換積分では、 $x=\sin \theta$ と置くことの方が多いです。こうすると $\cos $ を使うより、計算が少し計算が楽になります。このとき、積分区間は
\begin{array}{c|ccc} x & 0 & \cdots & 1 \\ \hline \theta & 0 & \cdots & \frac{1}{6}\pi \\ \end{array}となり、 $0$ が出てくるので、計算が少し楽になりそうな予感がしますね。さらに、 \begin{eqnarray} & & \int_0^1 \sqrt{4-x^2} dx \\[5pt] &=& \int_0^{\frac{\pi}{6} } 2\cos \theta \cdot 2\cos\theta d\theta \\[5pt] &=& \int_0^{\frac{\pi}{6} } 4\cos^2 \theta d\theta \\[5pt] \end{eqnarray}を計算することになります。 $dx$ を $2\cos\theta d\theta$ に置き換えていますが、ここでもマイナスが出てこないので楽ですね。

このことから、 $\sqrt{a^2-x^2}$ が被積分関数にあるときは、 $x=a\sin\theta$ と置いて解くとうまくいくことが多いです。