【標準】75度や150度の作図

ここでは、75度や150度を作図する方法を見ていきます。

特定の角の作図

作図の問題では、「 $\angle \mathrm{ PAB }=75^{\circ}$ となるように、点 P を作図しなさい」というように、特定の角度が指定されることもあります。分度器があれば楽なのですが、コンパスと定規だけで作図するにはどうすればいいでしょうか。

まず、【基本】作図で使う定規とコンパスで見たように、60度を作図することはできます。

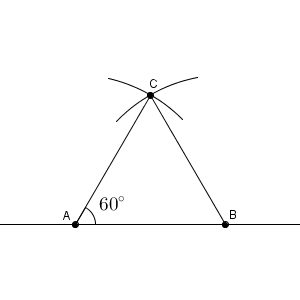
上のように、 A, B を中心とし、線分 AB の長さと等しい半径で円をかいて交点を C とすると、三角形 ABC は正三角形です。なので、60度を作り出すことができます。

また、直線をひけば、180度が作れます。【基本】垂線の作図（直線上の点を通る）で見たように、垂直な線を作図することもできるので、90度も作図できます。

さらに、角の二等分線の作図も使えば、今まで出てきた角の半分の角を作図することもできます。なので、60度の半分の30度やそれをさらに半分にした15度、また、90度の半分の45度を作図することができます。

これらを組み合わせて、75度や150度を作図する方法を考えてみましょう。

１５０度の作図

まずは、150度のほうから考えてみます。先ほど挙げた角を組み合わせて、150度を作るにはどうすればいいか考えてみましょう。

やり方はいろいろあります。１つの方法は、150度を90度と60度の和だと考える方法です。まず、90度を作図します。点 A を通り、線分 AB に垂直な直線をかきます。

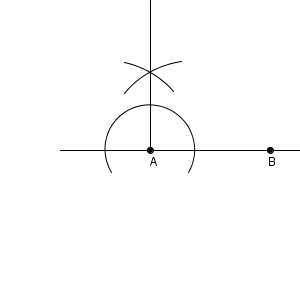
90度が作図できたら、正三角形を作るようにして60度を作図します。正三角形の1辺の長さは何でもいいですが、すでにあるものを使いまわしましょう。

垂線の左側に正三角形ができるように作図しました。こうして150度を作図することができます。

また、120度と180度を半分に分ける線を作図する、という考え方もあります。次のように正三角形を作るようにすると、 $\angle \mathrm{ BAC }=120^{\circ}$ となります。

さらに、角の二等分線を作図すれば、150度ができあがります。同じ長さの半径を使えば、ひし形ができることから150度ができることがわかりやすくなると思います。

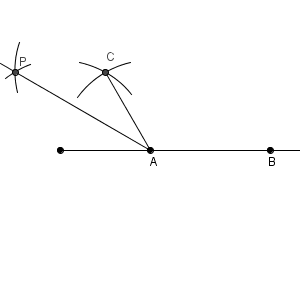
他にも方法はあると思いますが、このようにして、 $\angle \mathrm{ PAB }=150^{\circ}$ を作ることができます。

７５度の作図

45度と30度を足す、と考えてもいいですが、45度を作るには、180度と90度を作らないといけないし、30度は60度を作らないといけないため、作図するものが多くなります。この分割方法は思いつきやすいですが、作図は大変になってしまいます。

また、150度の半分と考える方法もありますが、これも少し遠回りです。150度の作図を見た後だから思いつきやすいかもしれませんが、75度と聞いて「150度の半分」と考えるのは少し難しいかもしれません。

先ほどの150度の作図でも見た通り、60度を作るのはわりと楽でした。正三角形を作るのはそれほど大変ではありません。そのため、60度を利用して、60度と15度に分けて考えてみることにしましょう。

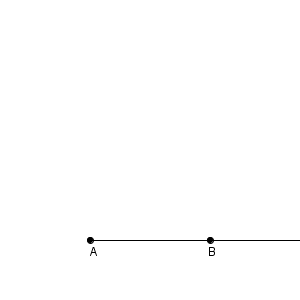
60度を作図するには、正三角形を作るようにすればいいですね。線分 AB の長さの正三角形を作図することで、 $\angle \mathrm{ CAB }=60^{\circ}$ となります。

残りの15度を作るのは大変そうですね。60度の半分の半分ですからね。ただ、追加で60度を作図するのはそれほど大変ではありません。次のようにすればOKです。

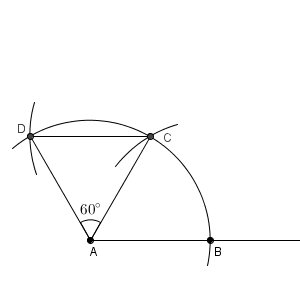
A, C を中心として、線分 AB と同じ長さの半径の円をかけばいいんですね。点 A を中心とする円は、先ほどのを使いまわせばいいです。 $\angle \mathrm{ CAD }=60^{\circ}$ なので、これで追加の60度が完成です。

60度の二等分線は、 C, D を中心として、同じ長さの半径を使いまわせばいいです。交点を E とします。

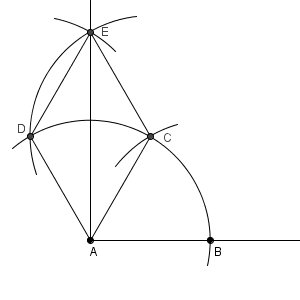
四角形 ACED はひし形で、 $\angle \mathrm{ EAC }=30^{\circ}$ となります。

あとは、15度です。さらに半分にすればいいですね。弧 CD と AE との交点を F として、 C, F を中心とした円をかきます。半径は AB の長さと同じでいいです。

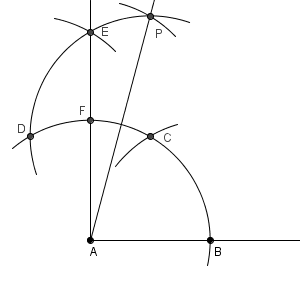
この直線上に点 P をとると、 $\angle \mathrm{ PAC }=15^{\circ}$ です。なので、 $\angle \mathrm{ PAB }=75^{\circ}$ となることがわかります。

上の図のすべての弧は、同じ半径です。そのため、コンパスの幅はすべて同じにしたまま作図できます。手順が多いので、方針をきちっと立ててから作図するようにしましょう。

なお、上の図では説明のために点に名前をつけていますが、実際の作図では、名前をつけるのは点 P だけでかまいません。

おわりに

ここでは、75度や150度の作図方法を見てきました。180度や60度を利用して、これらの半分の角や合わせた角を作って作図しました。手順が多くなるので、方針を立ててから作図しましょう。でないと、何度もかいたり消したりしないといけなくなります。