【応用】折り目の作図
ここでは、図形を折ったときの折り目を作図する問題を見ていきます。折り目が指定された点を通るように指示されている問題を扱います。
折り目の作図の復習
折り目の作図は、【標準】折り目の作図でも見ました。次のような問題です。
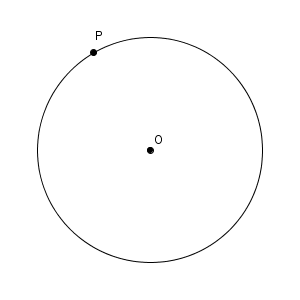
上の図で、点 P が点 O と重なるように折ったときの折り目を作図してみましょう。
折り返す前と折り返した後の図形(下の図の青と赤の部分)は同じなので、折り目は対称の軸になっている、というのがポイントでした。
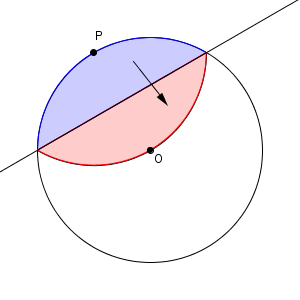
なので、線分 OP の垂直二等分線が折り目となります。
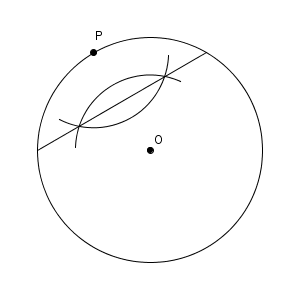
このことを踏まえて、折り目を作図する別のタイプの問題を考えてみましょう。
折り目の作図その1
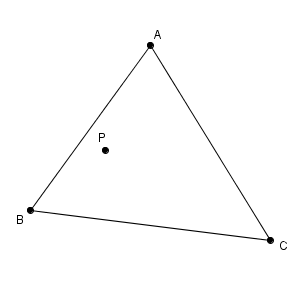
今回は、折った後に点 A がどこに行くのかがわかりません。辺 BC 上のどこか、ということしかわからないので、先ほどのように垂直二等分線をかくことができません。
一方、折り目が点 P を通る、という条件が加わっています。これをどのように使えばいいでしょうか。
頭の中でどのように折ればいいかをイメージして、完成図から考えてみましょう。完成図は次のようになります。

青い部分を折り返すと、赤い部分のようになります。折り目は点 P をとおり、点 A は辺 BC 上の点に移動していますね。
先ほども見た通り、折り返す前と折り返した後の図形は同じなので、折り目は対称の軸になっています。点 P は折り目の上にある、つまり、対称の軸上にあります。このことから、折り返した後に点 A が点 D に移動したとすると、AP と DP は同じ長さになります。
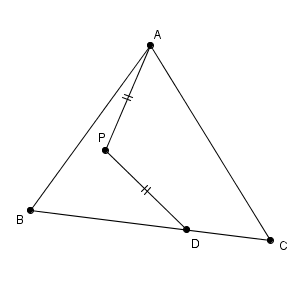
言い換えると、点 D は、点 P を中心とした、半径 AP の円周上にある、ということですね。なので、この円と辺 BC との交点が点 D となります。点 A が点 D に移動するのだから、あとは冒頭で見たように、線分 AD の垂直二等分線をかくと、それが折り目となります。これで完成です。
ここまでの内容を使って作図をすると次のようになります。
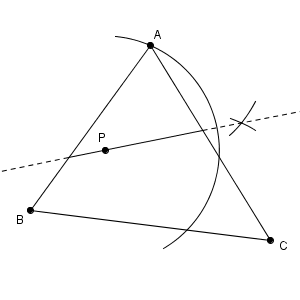
点に名前をつけて手順を書いていきます。

点 P が中心で半径 AP の円と辺 BC との交点を D とします。先ほど見た通り、折り返すと、点 A は点 D に移ります。
折り目を作図するには、線分 AD の垂直二等分線をかけばいいのですが、点 P を通ることがわかっているので、もう1点を作図するだけでいいですね。2点 A, D を中心として同じ半径の円をかいて、交点を作図します。この交点を Q とすると、点 P, Q を結べば、完成です。この直線上に折り目があります。
折り目の作図その2
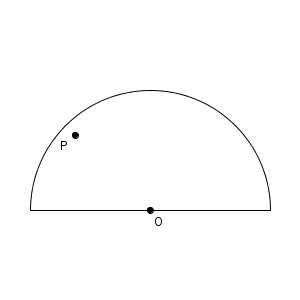
今回は、折り返した後の点 O がわかっていますが、折り返す前に対応する点がどこかがわかりません。ただ、先ほどの例題と同じように考えれば思いつきやすいでしょう。
先ほどの例題では、折り返す前の点がわかっていましたが、折り返した後にどこに移動するかはわかりませんでした。しかし、折り目が対称の軸になっていることを利用して、移動後の点がどこか、作図することができましたね。
今回の問題でも、同様の考え方を利用します。折り目が対称の軸となっており、点 P が対称の軸上の点です。円周上の点 A が点 O に重なるとすると、 $\mathrm{ AP=OP }$ が成り立つということなので、次のように作図できます。

あとは、点 A, O を中心とし、同じ半径の円をかき、交点と点 P とを結べばいいですね。こうすると線分 AO の垂直二等分線ができます。これが折り目となります。
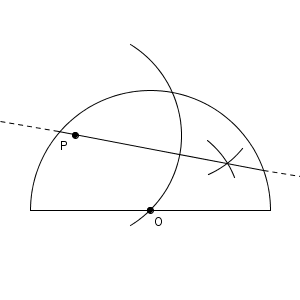
このように、折り目が対称の軸であることを利用して作図をします。
おわりに
ここでは、折り目がある点を通る、という条件のついた折り目の作図問題を見てきました。折り返しによって対応する点がどこに移動するかを求めてから作図します。折り目が対称の軸になっていることを利用して考えるようにしましょう。





