🏠 Home / 中学1年 / 平面図形（中学） / 基本の作図

【応用】90度に関連する作図

🕒 2019/08/08 🔄 2023/05/01

ここでは、接線や垂線などの90度に関連する作図を、別の見方で作図する方法を考えていきます。

📘 目次

円の接線の作図

円と接点が与えられている状況で、接線を作図する方法をもう一度考えてみます。

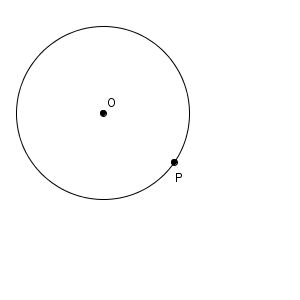
【基本】円の接線の作図で見たように、「円の中心と接点を結んだ直線に垂直な直線をかく」という方針で、次のように作図するのでした。

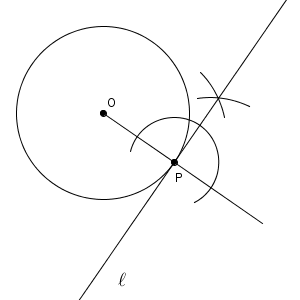
これでももちろんいいのですが、別のやり方もあります。それは、90度を60度と30度にわけて作図する方法です。60度は正三角形を使えば簡単に作図できます。これを利用します。

なぜこれで作図できるか、というのは後で書きますが、まずは作図したものを見てみましょう。

手順を説明します。まず、点 P を中心として点 O を通る円をかきます。2つの円の交点を A とします。点 A を中心として、点 P を通る円をかきます。この円と直線 AO の交点を Q とします。すると、直線 PQ が接線となります。

なぜこれで接線がかけるのか考えてみましょう。まず、三角形 AOP が正三角形になることがわかります。すべての辺の長さが同じだからですね。なので、 $\angle \mathrm{ APO }=60^{\circ}$ となります。

さらに、三角形 PAQ は二等辺三角形で、 $\angle \mathrm{ PAQ }=120^{\circ}$ だから、 $\angle \mathrm{ APQ }=30^{\circ}$ となります。

以上から、 $\angle \mathrm{ OPQ }=\angle \mathrm{ APO }+\angle \mathrm{ APQ }=90^{\circ}$ となります。こうして接線が作図できていることがわかります。

直線上の点を通る垂線の作図その１

ところで、【基本】円の接線の作図では、直線上の点を通る垂線の作図を利用して作図したのでした。ここでは、上で見た作図方法を逆に用いて、直線上の点を通る垂線の作図をやってみましょう。

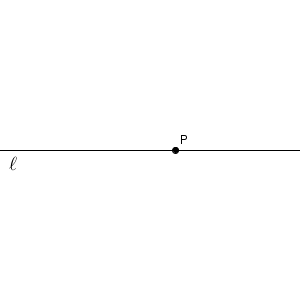
上の図で、まずは正三角形（の頂点）を作りましょう。点 P を中心とした円をかきます。半径は適当でいいです。直線 $\ell$ との交点を O とし、これを中心として先ほどと同じ半径の円をかきます。交点を A とすれば、三角形 AOP は正三角形です。

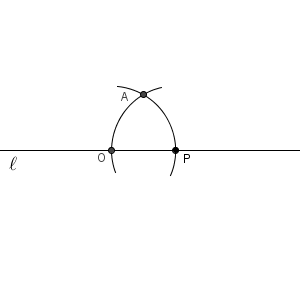
点 A を中心とした円をかき、 OA との交点を Q とすると、先ほどと同じ理由で、直線 PQ は直線 $\ell$ は垂直になります。

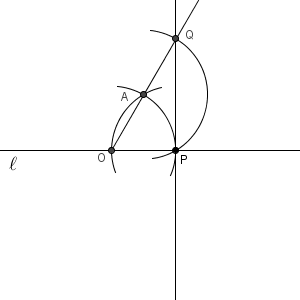
このようにしても、直線上の点を通る垂線の作図を行うことができます。

直線上の点を通る垂線の作図その２

先ほど、直線上の点を通る垂線の作図を、「60度と30度」に分解して作図する方法を見ました。実は、この分解は別の方法もあります。教科書で紹介されていることはほとんどありませんが、次のようにして作図することもできます。

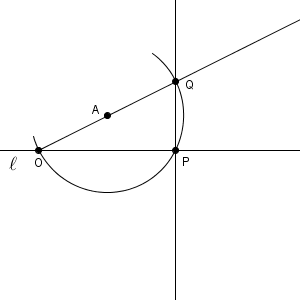
説明するために点に名前をつけていますが、実際には点の名前は書く必要はありません。

作図の手順を説明します。

まず、直線 $\ell$ 上にはない点を適当にとります。これを点 A としましょう。点 A を中心として点 P を通る円をかきます。この円と直線 $\ell$ との交点を O とします。円と直線 AO との交点を Q とすると、直線 PQ がかきたかった直線となります。

なぜこれで作図できているのか、すぐにはわかりづらいですね。次のように AP を結んで考えてみます。

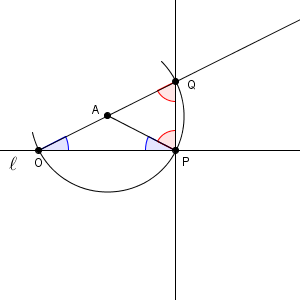
まず、三角形 APQ も三角形 APO も、二等辺三角形であることがわかります。なので、上の図の青い角、赤い角は同じ大きさです。

また、2つの青い角と2つの赤い角を足すと、三角形の角をすべて足したものになるので、180度になることがわかります。

よって、青い角と赤い角を1つずつ足せば、90度となります。 $\angle \mathrm{ OPQ }$ は青い角と赤い角を1つずつ足した角なので、 $\angle \mathrm{ OPQ }=90^{\circ}$ となることがわかります。つまり、 PQ は直線 $\ell$ と垂直であることがわかります。

先ほどの方法では、点 A は正三角形の頂点となるようにとりましたが、今回の方法では、
はじめにとった点 A は、直線 $\ell$ 上にない点であれば自由に選ぶことができます。

ここで見た作図方法は、将来学ぶ「円周角の定理」に関連した内容です。そのため、今の時点で教科書などで紹介されることはほとんどありませんが、このような作図方法がある、ということも知っておくと視野が広がると思います。