【基本】放物線と媒介変数表示

🕒 2018/05/27 🔄 2023/05/01

ここでは、放物線を媒介変数表示で表すとどうなるかを見ていきます。

📘 目次

放物線となる軌跡と媒介変数表示

【標準】軌跡（放物線の頂点）#放物線の頂点の軌跡その２でも見た、次の問題を考えてみましょう。

例題

実数 t が変化するとき、放物線 $y=x^2-2(t+1)x-2t+1$ の頂点の軌跡を求めなさい。

この放物線の頂点は
\begin{eqnarray} y &=& \{x-(t+1)\}^2-(t+1)^2-2t+1 \\[5pt] &=& \{x-(t+1)\}^2-t^2-4t \\[5pt] \end{eqnarray}だから、 $(t+1,-t^2-4t)$ となることがわかります。よって、 $(x,y)$ が軌跡上の点であるとすると、 \begin{eqnarray} x &=& t+1 \\[5pt] y &=& -t^2-4t \end{eqnarray}となることがわかります。この2つから $t$ を消せば、求める軌跡は\[ y=-x^2-2x+3 \]であることがわかります。

ところで、途中で出てきた、
\begin{eqnarray} x &=& t+1 \\[5pt] y &=& -t^2-4t \end{eqnarray}は、【基本】媒介変数表示で見たように、 $y=-x^2-2x+3$ の媒介変数表示になっている、とも考えられるわけですね。

このように、軌跡の分野で考えていた内容は、「媒介変数表示された式から、x, y が満たす関係式を求める問題」だったととらえられるものも含まれていました。

放物線の標準形と媒介変数表示

【基本】放物線の焦点と準線で見たように、 $p\ne0$ のとき、 $y^2=4px$ のグラフは、点 $(p,0)$ を焦点とし、直線 $x=-p$ を準線とする放物線となります。この形 $y^2=4px$ を放物線の標準形と呼びます。

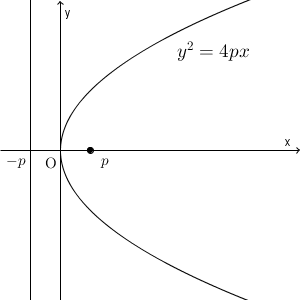
この放物線に対し、直線 $y=2pt$ との交点を考えてみましょう。これは、 x 軸に平行な直線で、 t を動かすことで、上下に移動します。 $2pt$ の $2p$ がどこから来たのか、はあとで考えるとして、ひとまず交点を求めてみます。

交点の x 座標は
\begin{eqnarray} (2pt)^2 &=& 4px \\ x &=& pt^2 \\ \end{eqnarray}となります。よって、この放物線上の点は、媒介変数 t を用いて \begin{eqnarray} x &=& pt^2 \\[5pt] y &=& 2pt \\[5pt] \end{eqnarray}と書くことができます。 $y=2pt$ としましたが、 $y=t$ や $y=pt$ とすると、 $x$ の式に分数が出てきてしまいます（実際に上の式に代入してみましょう）。そのため、わざわざ $2p$ をつけていたわけですね。

媒介変数表示は1通りではないので、上の表し方は、媒介変数での表示の一例、となります。

もし、上と同じように表すのであれば、 $y^2=-8x$ は、 $p=-2$ とすればよく、
\begin{eqnarray} x &=& -2t^2 \\[5pt] y &=& -4t \\[5pt] \end{eqnarray}と表されることになります。実際に $t$ を消去すると、元に戻りますね。

ここでは、まだ媒介変数表示をする必要性、メリットがよくわからないと思いますが、複雑な例を理解するための練習だと思っていてください。