【基本】楕円と媒介変数表示

🕒 2018/05/30 🔄 2023/05/01

ここでは、楕円を媒介変数表示するとどうなるかを見ていきます。

📘 目次

楕円の媒介変数表示

楕円は、以下のような形をした図形でしたね。

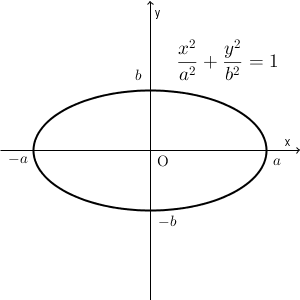
$x,y$ を使って書くと、 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ となります（参考：【基本】楕円の焦点（焦点がx軸上））。また、形を見ても想像できますが、楕円は円を拡大・縮小したものになります（参考：【基本】楕円の方程式と円の方程式）。

以上から、楕円の媒介変数表示は、楕円を拡大・縮小し、円の媒介変数表示を利用する方向で考えるとわかりやすいです。

楕円上の点 $\mathrm{ P }(x,y)$ に対して、次のように対応付けされる点 $\mathrm{ Q }(X,Y)$ を考えてみましょう。
\begin{eqnarray} X=\frac{x}{a},\ Y=\frac{y}{b} \end{eqnarray}

このとき、 $X^2+Y^2=1$ なので、点 Q は単位円の円周上にあります。

【基本】円と媒介変数表示でも見たように、単位円は、次のように媒介変数表示で表すことができます。
\begin{eqnarray} X &=& \cos\theta \\[5pt] Y &=& \sin\theta \end{eqnarray}よって、楕円上の点 $\mathrm{ P }(x,y)$ は、次のように表すことができます。 \begin{eqnarray} x &=& a\cos\theta \\[5pt] y &=& b\sin\theta \\[5pt] \end{eqnarray}楕円上のすべての点が表せるので、この表し方は楕円の媒介変数表示だということができます。

具体的な例でいえば、 $\dfrac{x^2}{9}+\dfrac{y^2}{16}=1$ なら
\begin{eqnarray} x&=&3\cos\theta \\[5pt] y&=&4\sin\theta \end{eqnarray}と表すことができる、ということですね。係数をうまく選んで $\cos^2\theta+\sin^2\theta=1$ となるようにすればいいので、思い出すのもそれほど難しくはないでしょう。

なお、媒介変数表示に出てくる $\theta$ は、上の図での OP と x 軸とのなす角ではないことに注意しましょう。 $\theta$ は、 OQ と x 軸とのなす角です。楕円上の点と原点とを結んでも、 $\theta$ が直接出てくるわけではありません。