【標準】アステロイドと媒介変数表示

🕒 2018/06/03 🔄 2023/05/01

ここでは、アステロイドという図形を紹介し、この媒介変数表示について見ていきます。

📘 目次

アステロイド

【基本】サイクロイドと媒介変数表示では、円が直線の上を転がるときに、円周上のある点の軌跡をサイクロイドと呼ぶことを見ました。アステロイドは、サイクロイドと似ているのですが、違いは、直線上ではなくある円の内側を転がるところです。

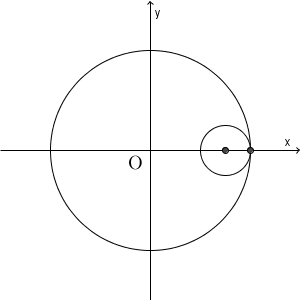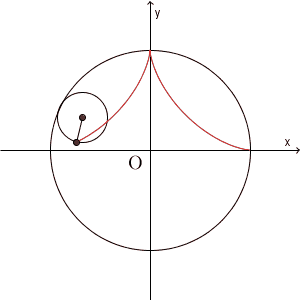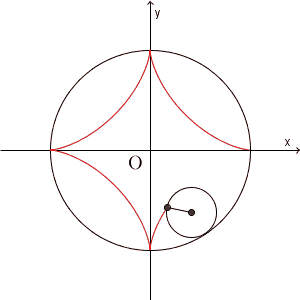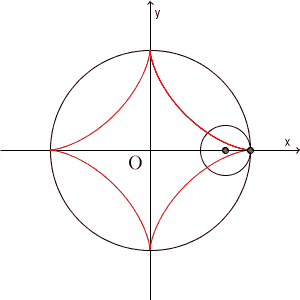
アステロイド(astroid) とは、上の図のように、ある円の円周に沿って、その $\dfrac{1}{4}$ の半径の円が、内側を滑ることなく回転するとき、円周上のある点が描く曲線のことを言います。名前の astroid は、 aster(星の), oid(のようなもの)という意味です。asterは、star(星)にも関連しています。日本語では、星芒形（せいぼうけい）と呼ばれることもありますが、アステロイドと呼ばれることの方が多いでしょう。

内側で動く円の半径が、外側の円の半径の $\dfrac{1}{4}$ である、という条件は重要です。違う大きさであれば、軌跡は別の形となってしまいます。

アステロイドの媒介変数表示

さて、アステロイドの媒介変数表示を考えてみましょう。サイクロイドのときと同じように、動いている円の中心や接点などに注目して考えていきます。以下では、外側の円の半径を $1$ 、内側の円の半径を $\dfrac{1}{4}$ として考えていきます。

$\mathrm{ A }(1,0)$ とし、はじめ、2つの円は点 A で接していたとします。この点 A にあった点が、回転により、点 P に移動しているとします。また、2つの円の接点を B, 動いている円の中心を C とします。このとき、 O, C, B は一直線上にあることに注意しましょう。

$\angle \mathrm{ COA }=\theta$ とすると、 $\mathrm{ OC }=\dfrac{3}{4}$ であることから、 C の座標は\[ \left(\dfrac{3}{4}\cos\theta, \dfrac{3}{4}\sin\theta\right) \]であり、 B の座標は\[ (\cos\theta, \sin\theta) \]となります。

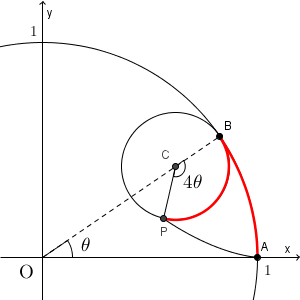
また、滑ることなく内側の円が回転していることから、内側の円における弧 BP の長さと、外側の円における弧 AB の長さは同じです。弧 AB の長さは $\theta$ であり、 $\mathrm{ BC }=\dfrac{1}{4}$ だから $\angle \mathrm{ BCP }=4\theta$ となります。

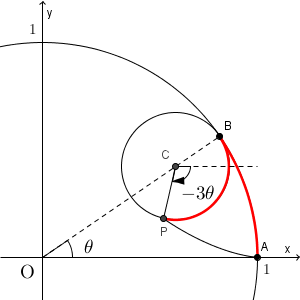
よって、 P は、 C を中心に B を時計回りに $4\theta$ だけ回転した点だから、 CP と x 軸の正の向きとのなす角は $-3\theta$ となります。

以上から、 P の x 座標は
\begin{eqnarray} & & \dfrac{3}{4}\cos\theta+\dfrac{1}{4} \cos(-3\theta) \\ &=& \dfrac{1}{4}(3\cos\theta+\cos 3\theta ) \\ &=& \dfrac{1}{4}(3\cos\theta-3\cos \theta+4\cos^3\theta ) \\ &=& \cos^3\theta \\ \end{eqnarray}となります。なお、途中で【標準】3倍角の公式を使っています。 y 座標は \begin{eqnarray} & & \dfrac{3}{4}\sin\theta+\dfrac{1}{4} \sin(-3\theta) \\ &=& \dfrac{1}{4}(3\sin\theta-\sin 3\theta ) \\ &=& \dfrac{1}{4}(3\sin\theta-3\sin \theta+4\sin^3\theta ) \\ &=& \sin^3\theta \\ \end{eqnarray}となります。

よって、アステロイド上の点の座標は $(\cos^3\theta,\sin^3\theta)$ と書くことができます。これですべての点が表せているので、これがアステロイドの媒介変数表示となります。

なお、2つの円の半径を $a$, $\dfrac{1}{4}a$ としたときは、弧の長さなどをすべて $a$ 倍すればいいので、この場合のアステロイド上の点の座標は、 $(a\cos^3\theta,a\sin^3\theta)$ となります。

また、アステロイドの場合は、サイクロイドの場合とは異なり、曲線を $x,y$ だけの式できれいに表すことが可能です。 $\cos^2\theta+\sin^2\theta=1$ が一般的に成り立つことから、アステロイド上の点 $(a\cos^3\theta,a\sin^3\theta)$ は、\[ x^{2/3}+y^{2/3}=a^{2/3} \]を満たします。これは、アステロイドを表す方程式となります（厳密にいえば、これを満たす点がアステロイド上にあることを示す必要がありますが、ここでは省略します）。