【基本】双曲線と媒介変数表示（最もシンプルな場合）

🕒 2018/05/31 🔄 2023/05/01

ここでは、最もシンプルな双曲線を媒介変数表示するとどうなるかを見ていきます。

📘 目次

双曲線の媒介変数表示を特別な例で考える

【基本】円と媒介変数表示や【基本】楕円と媒介変数表示で見たように、円や楕円は、一般角の三角関数を使って媒介変数表示をすることができました。双曲線も同じように三角関数を使って表してみましょう。

双曲線は、 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ といった形で表されますが、このうち、もっとも単純な双曲線は、 $x^2-y^2=1$ です。 $a=b=1$ とした場合ですね。まずは、この双曲線について考えてみましょう。

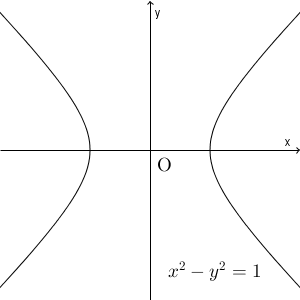
円の場合は、単位円の方程式 $x^2+y^2=1$ と三角比の相互関係 $\sin^2\theta+\cos^2\theta=1$ とを関連付けて、媒介変数表示に利用できました。双曲線 $x^2-y^2=1$ の場合は、このままでは相互関係と関連付けることはできませんが、次のように変形してみるとどうでしょう。\[ 1+y^2=x^2 \]こうすれば、相互関係の $1+\tan^2\theta=\dfrac{1}{\cos^2\theta}$ と形が似ていますね。なので、 $x=\dfrac{1}{\cos\theta}$, $y=\tan\theta$ と書けるんじゃないか、と予想できます。

実際、このように置くと、 $x^2-y^2=1$ を満たすことがわかります。また、 $\theta$ が $-\dfrac{\pi}{2}$ から $\dfrac{\pi}{2}$ まで動く（両端は除く）と、 $\dfrac{1}{\cos\theta}$ は1以上のすべての値をとり、 $\tan\theta$ はすべての実数値を取ります。 $\theta$ が $\dfrac{\pi}{2}$ から $\dfrac{3\pi}{2}$ まで動く（両端は除く）と、 $\dfrac{1}{\cos\theta}$ は-1以下のすべての値をとり、 $\tan\theta$ はすべての実数値をとります。つまり、 $\theta$ が動けば、上のように表した点 $(x,y)$ は、双曲線 $x^2-y^2=1$ 上のすべての点を表せることがわかります。よって、
\begin{eqnarray} x &=& \dfrac{1}{\cos\theta} \\[5pt] y &=& \tan\theta \end{eqnarray}は、双曲線の媒介変数表示となります。

ただ、なんだかスッキリしない感じでしたね。この $\theta$ が双曲線上の点とどう対応しているのか、図形的な観点から確認しましょう。

双曲線の媒介変数表示を図形的に考える

さて、先ほど、双曲線 $x^2-y^2=1$ に対して、 $x=\dfrac{1}{\cos\theta}$, $y=\tan\theta$ が媒介変数表示となっていることを見ました。これを図形的に確認してみましょう。

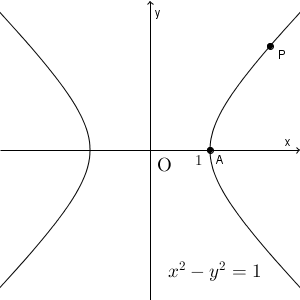
$\mathrm{ A }(1,0)$ とします。双曲線上の点 $\mathrm{ P }(x,y)$ について考えます（第1象限にあるときを考えますが、他の場合も同様です）。この $y$ 座標が $\tan\theta$ になることから、 $\theta$ は $\mathrm{ B }(1,y)$ と原点とを結んだ線分と、 x 軸の正の向きとがなす角であることがわかります。

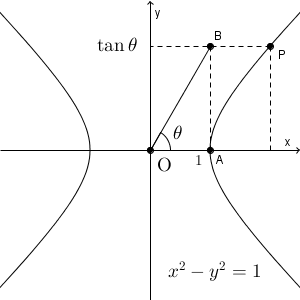
y 座標から $\theta$ は上のように対応します。この $\theta$ を使って、今度は P の x 座標を考えてみましょう。 x 座標は $\dfrac{1}{\cos\theta}$ となるわけですが、図形的には次のように線をひけばわかります。

先ほどの $\mathrm{ OB }$ が単位円と交わる点を C とします。この $\mathrm{ C }(\cos\theta,\sin\theta)$ での単位円の接線をかいたのが上の図です。接線と x 軸との交点を D とすると、\[ \cos\theta=\dfrac{\mathrm{ OC } }{\mathrm{ OD } } \]であることから、\[ \mathrm{ OD }=\dfrac{1}{\cos\theta} \]となることがわかります。これが x 座標の式でしたね。

また、三角形 OAB と三角形 OCD が合同になっていることにも注意しましょう。

ここまでの流れを踏まえ、 $\theta$ から双曲線上の点がどう対応するかをまとめましょう。 $\mathrm{ C }(\cos\theta,\sin\theta)$ での単位円の接線を考え、この接線と x 軸との交点を D とおいたとき、三角形 OCD は、\[ \mathrm{ OC }=1, \mathrm{ CD }=\tan\theta, \mathrm{ DO }=\dfrac{1}{\cos\theta} \]の直角三角形であり、1以外の辺を使って\[ \left(\dfrac{1}{\cos\theta}, \tan\theta\right) \]と書けば、この点は双曲線 $x^2-y^2=1$ 上にあります。

このように双曲線上の点の x, y 座標は、1つの角が $\theta$ の直角三角形の斜辺と他の1辺に対応していることがわかります。